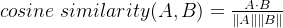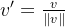余弦相似度的定义

对于两个词向量 A=[a1, a2, ..., an] 和 B=[b1, b2, ..., bn]，它们的余弦相似度定义为：

几何意义

余弦相似度衡量的是两个向量在空间中的方向相似度，而不是它们的长度（大小）。具体来说：

• 如果两个向量的方向完全一致，余弦相似度为 1。
• 如果两个向量的方向完全相反，余弦相似度为 -1。
• 如果两个向量完全不相关（正交），余弦相似度为 0。

为什么词向量（Word Embedding）的语义信息主要由向量的方向表示，而不是长度？

• 词向量中的每个维度对应着不同抽象的语义特征
  • 向量中的每个维度对应一个潜在的语义特征，如性别、年龄、职业等（但这些特征的具体含义通常是隐式的，无法直接解释）。
  • 例如，某个维度可能表示“性别”，另一个维度可能表示“食物”，这些特征共同决定了词向量的方向。
  • 例如，“man” 和 “woman” 在向量的性别维度取值相似，而向量的性别维度会对提高这两个向量的相关度有所贡献，从而使这两个词的向量方向接近。（以二维向量为例，假设这两个向量均以坐标轴原点作为起点，则在x取值相同的情况下，y值取值越相近，两个向量的夹角就越小，即方向越接近）

向量长度的影响

• 长度的随机性：词向量的长度在训练过程中是随机生成的，并不直接对应语义信息。因此，词向量的长度通常不反映词汇的语义特征。
• 长度的归一化：为了使词向量的方向成为唯一的语义表示，通常会对词向量进行归一化处理。
  • 归一化公式：
  • 归一化后的词向量长度为 1，语义完全由方向表示。
• 注意，此处的向量长度指的是向量的模长，而不是向量的维数。

归一化的作用

公式中的分母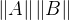的作用是：

• 将向量的长度（大小）标准化，只保留方向信息。
• 这样，即使两个向量长度不同，公式也能准确反映它们的方向相似度。

对比：欧式距离

欧氏距离不仅考虑了向量方向的差异，还考虑了向量长度的差异，因此欧式距离更适合度量图像相似度。

• 图像向量的长度（范数）反映了图像的整体亮度或强度。
  • 例如，灰度图像的全局亮度越大，对应的向量长度越大。
  • 彩色图像的向量长度则反映了颜色的整体强度。