💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
💥1 概述
快速探索随机树(Rapidly-exploring Random Tree,RRT)算法是一种常用于路径规划的概率型算法,特别适用于自动驾驶汽车的路径规划,能够有效地绕过静态障碍物。 RRT算法通过随机采样和快速扩展树结构来生成路径。 它以车辆当前位置为起点,随机采样可能的目标位置作为终点,并在树结构中搜索路径。 每次迭代,根据一定的策略,将新的节点添加到树中,以扩展树结构。 RRT算法不断迭代,直到生成路径连接起始点和目标点,或达到最大迭代次数。RRT算法作为一种概率型路径规划算法,在自动驾驶汽车的路径规划中具有重要应用,能够有效地绕过静态障碍物并生成可行的行驶路径。
一、引言
自动驾驶汽车的路径规划是实现无人驾驶的关键技术之一。在自动驾驶过程中,车辆需要准确地理解路况,选择最优路径,并避开障碍物。RRT算法作为一种概率型路径规划算法,因其较快的速度和较好的鲁棒性,在自动驾驶汽车的路径规划中具有重要意义。
二、快速探索随机树(RRT)算法简介
RRT算法是一种常用于路径规划的概率型算法。它以车辆的当前位置为起点,随机采样可能的目标位置作为终点,并在树结构中搜索路径。在每次迭代中,根据一定的策略将新的节点添加到树中,以扩展树结构。RRT算法不断迭代,直到生成连接起始点和目标点的路径,或达到最大迭代次数。
三、RRT算法在自动驾驶汽车路径规划中的应用
- 初始化:设定自动驾驶汽车的当前位置为RRT算法的起点,随机采样一个目标位置作为终点。同时,定义车辆的行驶环境和静态障碍物的位置。
- 节点扩展:在每次迭代中,从节点列表中选取一个最接近随机采样点的节点作为父节点,并向随机采样点方向扩展一个新的节点。在扩展过程中,需要检查新节点是否与静态障碍物发生碰撞。
- 路径搜索:当新节点被成功添加到树中时,更新其父节点和新节点之间的路径成本。然后,从起点开始,沿着父节点链回溯到目标点,形成一条完整的路径。
- 迭代终止:当生成的路径连接起始点和目标点,或达到最大迭代次数时,迭代终止。
四、RRT算法的优缺点及改进方法
-
优点:
- RRT算法具有较快的搜索速度,能够在较短时间内生成可行的行驶路径。
- RRT算法对环境的适应性较强,能够有效地绕过静态障碍物。
-
缺点:
- RRT算法生成的路径可能不是最优的,因为路径的生成依赖于随机采样点的选择。
- 在复杂环境中,RRT算法可能需要大量的迭代次数才能找到可行的路径。
-
改进方法:
- 引入启发式信息来指导随机采样点的选择,以提高路径的最优性。
- 使用双向RRT算法,从起点和终点同时生成树结构,以加快路径的生成速度。
五、实验验证与结果分析
为了验证RRT算法在自动驾驶汽车路径规划中的有效性,进行了以下实验:
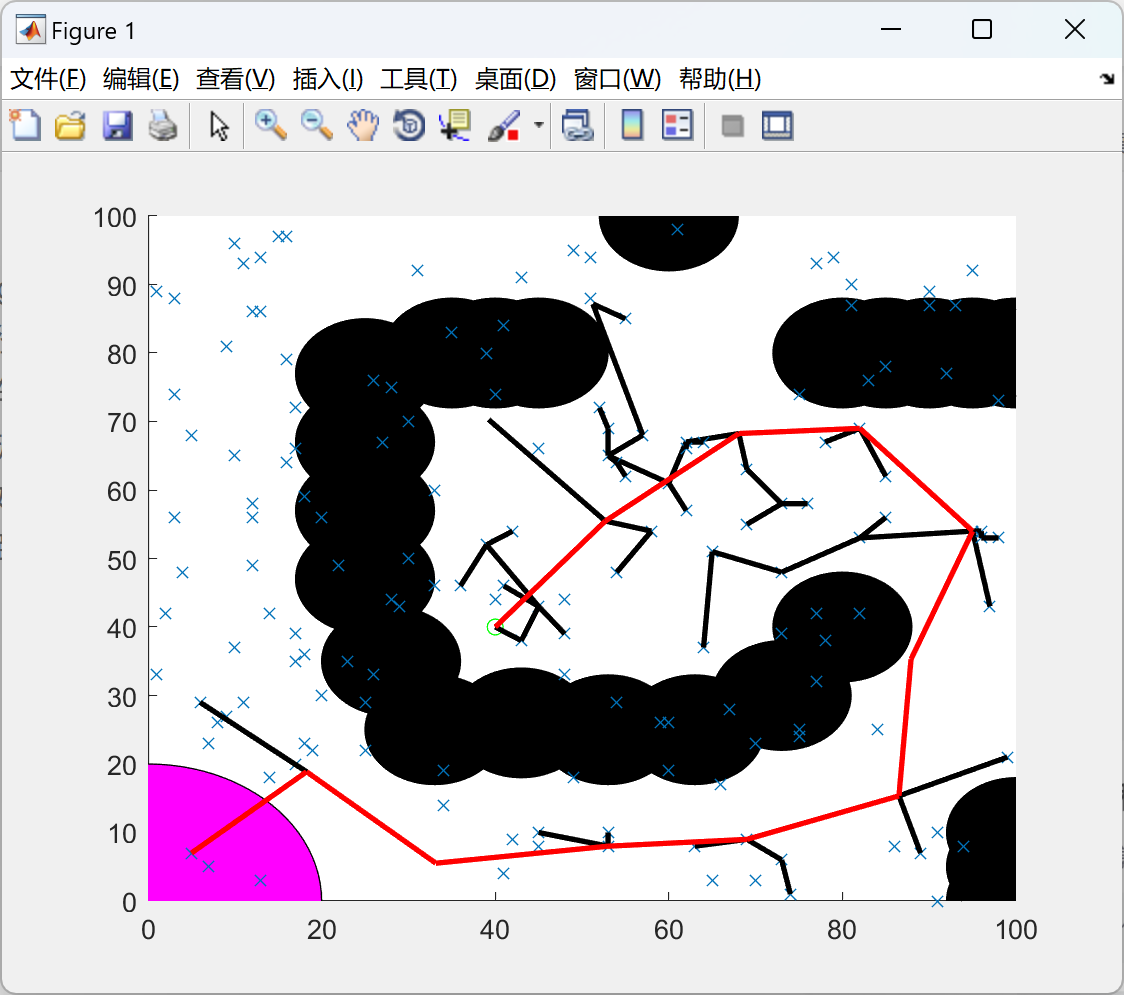
- 实验设置:设定一个包含静态障碍物的二维行驶环境,自动驾驶汽车的起点和目标位置已知。使用Matlab软件实现RRT算法,并生成行驶路径。
- 实验结果:实验结果表明,RRT算法能够在较短时间内生成避开静态障碍物的可行行驶路径。同时,通过调整算法参数,如最大迭代次数和随机采样点的选择范围,可以进一步优化生成的路径。
- 结果分析:RRT算法在自动驾驶汽车路径规划中具有广泛的应用前景。然而,在实际应用中还需要考虑车辆的动力学约束、交通规则等因素,以进一步提高路径的可行性和安全性。
六、结论与展望
本研究通过理论分析和实验验证,证明了RRT算法在自动驾驶汽车路径规划中的有效性。未来研究可以进一步探索RRT算法与其他路径规划算法的融合,以及考虑车辆动力学约束和交通规则等因素的路径规划方法,以进一步提高自动驾驶汽车的安全性和可靠性。
📚2 运行结果
主函数部分代码:
% RRT algorithm in 2D with disc obstacle avoidance.
% Anand Patel
%
% nodes: contains its coordinates, cost to reach, and its parent.
%
%
% How it works:
% 1. Pick a random node q_rand.
% 2. Find the closest node q_near from nodes list to branch out from
% towards q_rand.
% 3. Move from q_near towards q_rand: interpolate if node is too far away,
% reach q_new. Check for collisions.
% 4. Update cost of reaching q_new from q_near, Cmin. q_near
% acts as the parent node of q_new.
% 5. Add q_new to node list.
% 6. Continue until maximum number of samples is reached or goal region is
% entered.
clearvars
close all
% make S = [0 100] X [0 100]
x_max = 100;
y_max = 100;
% read in obstacles
obstacle_array = csvread('H3_obstacles.txt');
% turn array into struct
for j=1:1:23
obstacle(j).coord = [obstacle_array(j,1) obstacle_array(j,2)];
obstacle(j).rad = obstacle_array(j,3);
end
nodes_id = 1;
EPS = 20; % epsilon distance ASSIGNED
numNodes = 100000; % max number of samples taken
del_t = 10;
delta = .5;
q_start.coord = [40 40]; % start node's (x,y) coordinate ASSIGNED
q_start.cost = 0; % cost to reach start node set to 0
q_start.parent = 0; % parent of start node set to 0
q_start.id = nodes_id;
q_start.time = 0; % start node begins at t=0
q_start.theta = pi/4; % start node theta ASSIGNED
q_start.v = 0; % start node trans vel = 0
🎉3 参考文献
文章中一些内容引自网络,会注明出处或引用为参考文献,难免有未尽之处,如有不妥,请随时联系删除。
[1]金煦,莫愿斌.多策略混合山地瞪羚优化器在机器人路径规划问题中的应用[J/OL].系统仿真学报:1-18[2024-04-21].https://doi.org/10.16182/j.issn1004731x.joss.23-1392.
[2]牛旭,张志安.改进RRT的复杂障碍物环境路径规划算法研究[J].电子设计工程,2024,32(08):162-167+172.DOI:10.14022/j.issn1674-6236.2024.08.035.