点击上方蓝字“和乐数学”关注我们,查看更多历史文章。设为星标,快速读到最新文章。
作者 | math3ma 翻译 | 比特小组 转自 | 机器学习与数学 原文 | http://mrw.so/4pCURYA First Look at Quantum Probability, Part 1
在这个短文系列中,我将分享一些有关量子概率的想法。量子一词很有架势,但不要被它吓到了。我们仅仅是初探一下该主题,而不是深入研究它。因此,读者只需要掌握线性代数和基本的概率知识即可。实际上,我喜欢将量子概率论看成线性代数+概率论的代名词。而这个短文系列也将探讨有关该主题的数学知识,而非物理概念。
我们先谈论下经典概率以引出本文的论题。具体地,让我们来花一点时间思考一下下面这句话(边缘概率没有记忆),

明白它什么意思吗?下面我们先从一些基本定义开始,然后,我再分享一个具体例子来说明上面这个说法。
. 01 .回顾边缘概率
有限集 上的概率分布(或简称为分布)是满足 的函数 。我将使用术语联合概率分布来表示定义在有限集的笛卡尔积上的分布,即满足 的函数 。每个联合分布通过对其中一个集合的概率求和来定义另一个集合的边缘概率分布。例如,在 上的边缘分布 定义为 ,这里对变量 进行求和或积分了。正是这个求和或积分导致了信息的丢失。换句话说,边缘计算会丢失信息。因为它并不记得加了什么东西!
我将举一个简单例子来阐明这点。首先给定两个有限集 和 以及定义在其上的概率分布。
考虑所有长度为 3 的位串集合 。每个位串都以 0 或 1 开头,因此我们可以将 视作集合 与长度为 2 的位串集合 的笛卡尔积。可以方便地将 中的元素称为前缀, 中元素称为后缀。
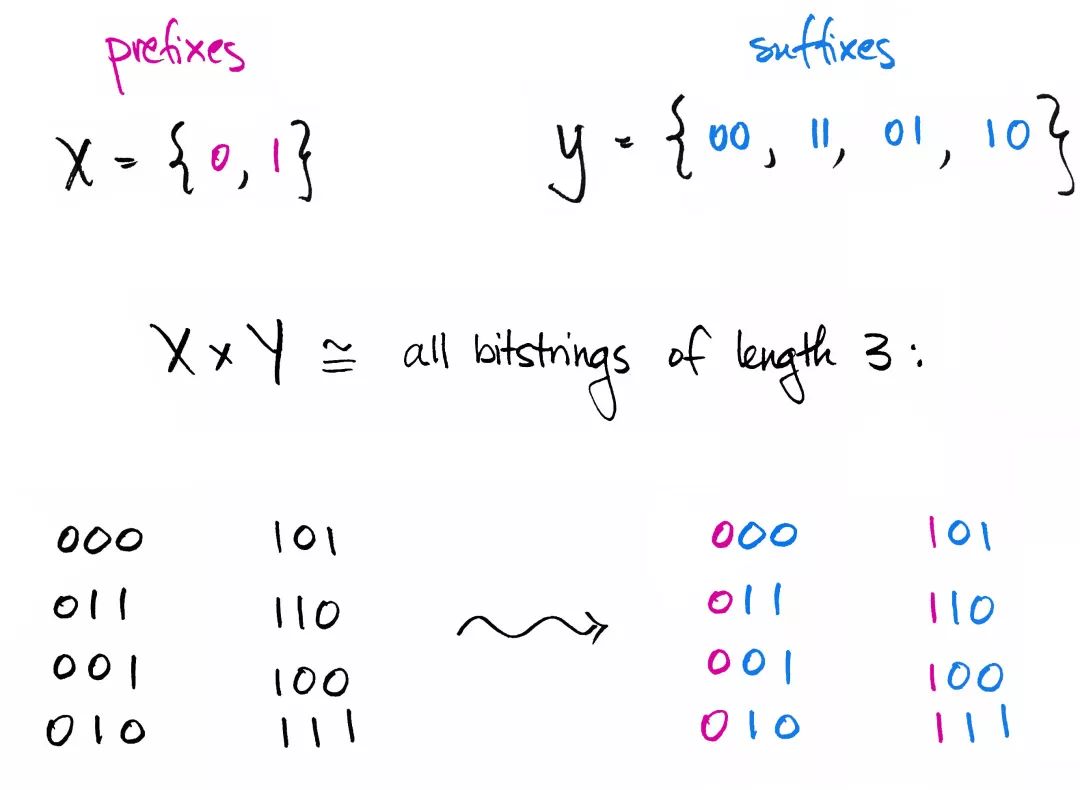
这里我们需要一个定义在 上的概率分布。假设 的概率为 , 的概率为 , 和 的概率均为 ,其他位串的概率为零。因此,你可以想象一个七面骰子,它各个面上的标记如下,
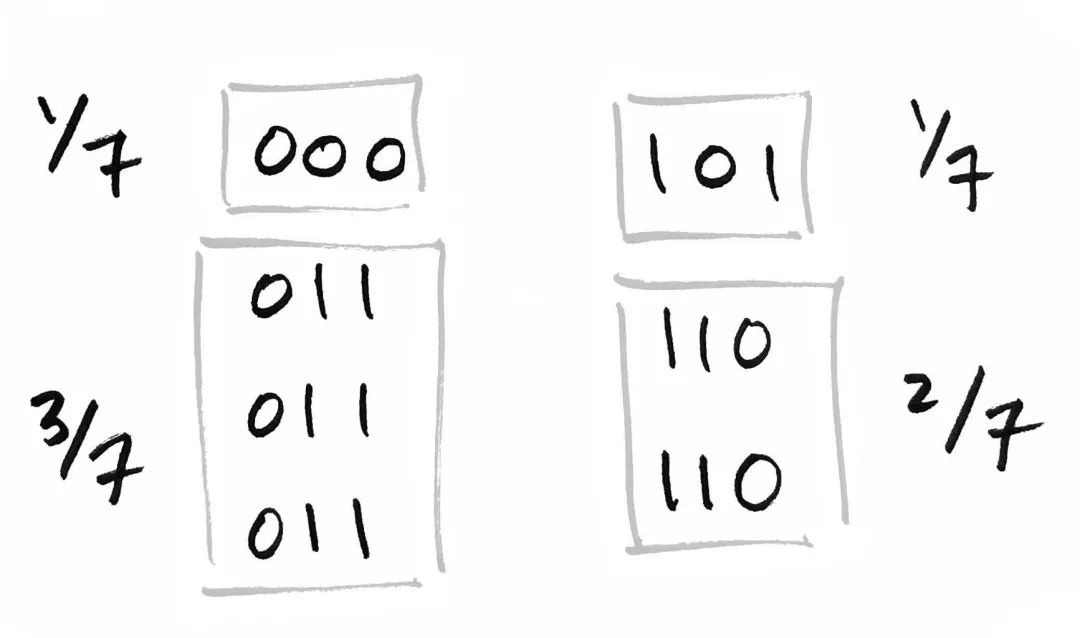
可视化该联合分布的一种办法是加权二分图。我们之前已经探讨过这个想法[1]。前缀集合和后缀集合定义了两组顶点(二分图 bipartite)。如果前缀和后缀的组合是一个样本,则用边将它们连接起来。该边的标记是对应的概率(加权)。查看联合分布的另一种办法是使用一张 表格。行对应 的元素,列对应 的元素,而位置 上的元素对应概率 。
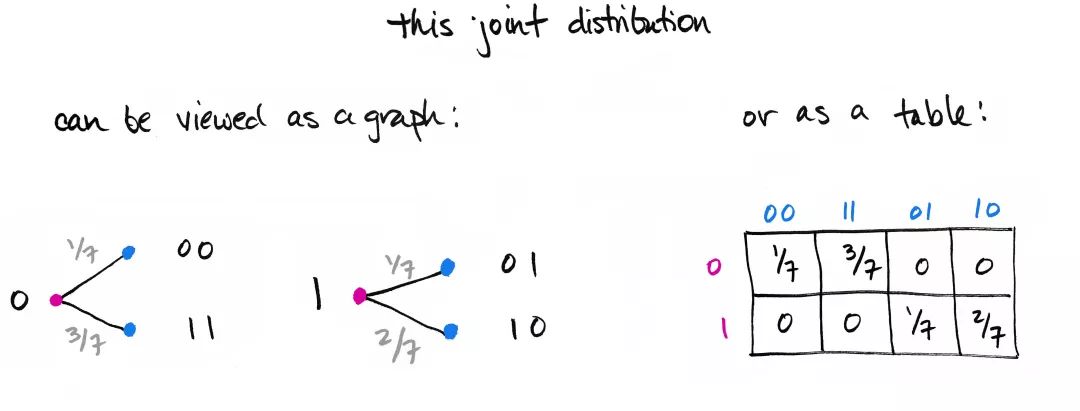
边缘概率很容易计算: 只需要沿表格的行或列求和!例如,后缀为 的概率为 。
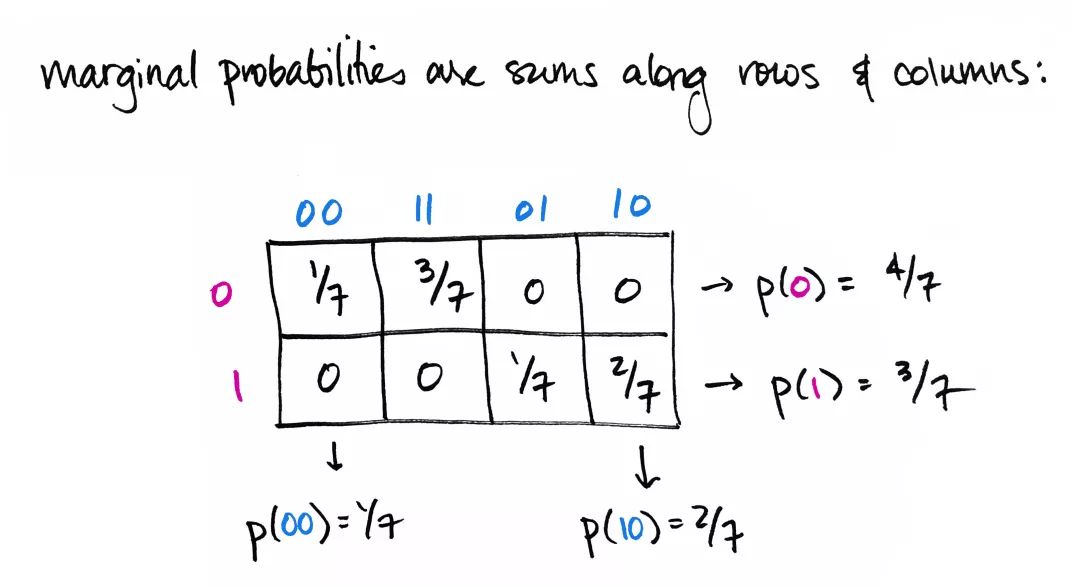
这里我要强调的一点是,边缘概率是不带记忆的。这句话具体是什么意思呢?我来解释一下,
- 前缀 的边缘概率为 ,但该数字并未告诉我们前缀 之后有哪些可能的后缀,即 个 , 个 , 个 以及 个 。
- 前缀 的边缘概率为 ,但该数字并未告诉我们前缀 之后有哪些可能的后缀,即 个 , 个 , 个 以及 个 。
换句话说,对 中的后缀求和使我们失去了 中信息。无法挽回,无法恢复。这就是我所说的边缘概率没有记忆。它仅仅是概率的一个特征。
. 02 .矩阵表示的边缘概率
我现在要介绍由联合分布计算边缘分布的另一种方法。可以将其看成带记忆的边缘概率。以这种新方式来计算边缘概率的话,我们可以获取按前面传统方式计算时丢失的信息!
这些想法很简单,尽管一开始可能会让你觉得这并没有什么道理。请耐心容忍我啰嗦一下,我想先给你看些好东西。之后我会解释到底怎么回事。
我们再次从联合分布开始。众所周知,它可以看成一张 的表格。
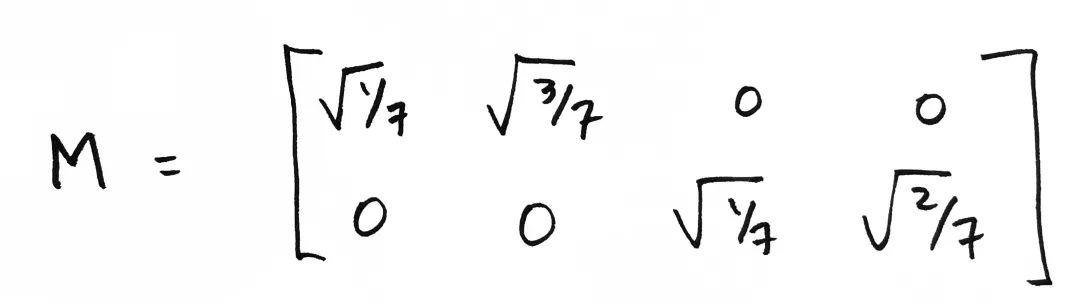
正如你看到的,我作了一些小修改。 的表格现在被我写成一个 的矩阵,并且我加上了一些根号。我加上它们仅仅是从数学上来考虑,你不必担忧这点,可以先忽略它们。最后,给矩阵起一个名字,。
现在让我们用 的转置乘以 ,得
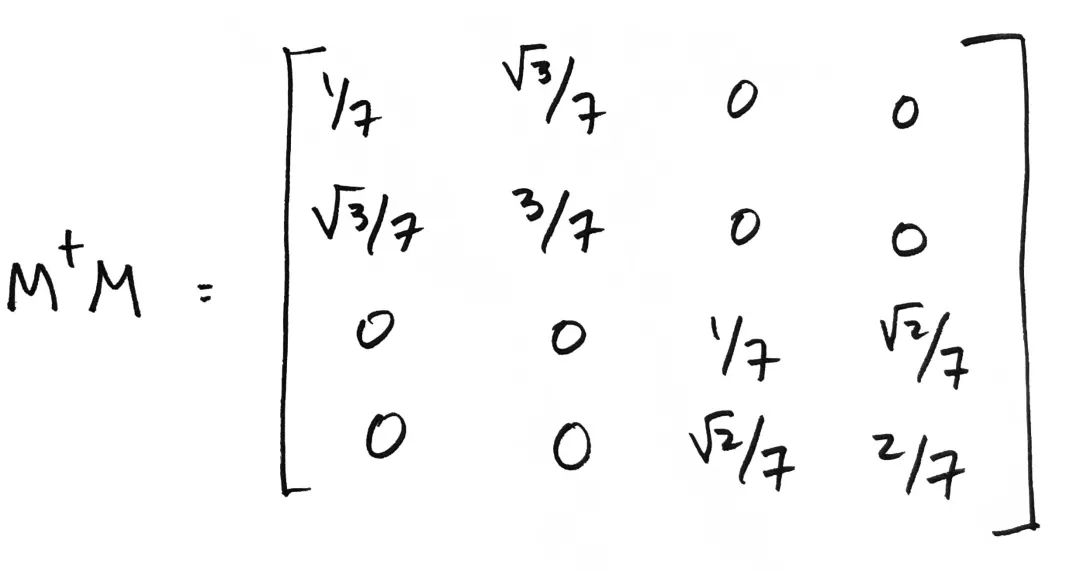
这个矩阵非常有趣。首先,它是一个 矩阵。我们可以通过此矩阵的行/列来识别集合 中包含的四个元素。这也为另一个观察奠定了基础,即矩阵 的对角线包含了 上的边缘概率分布。
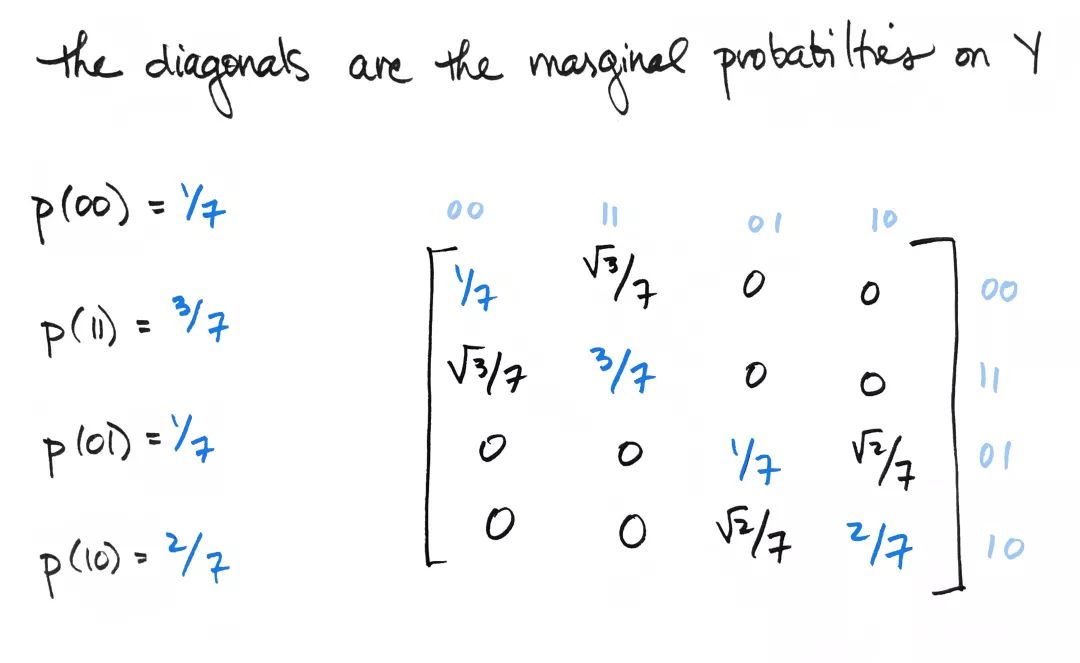
我们仅仅是用一个矩阵的转置乘以这个矩阵来计算边缘概率。另外,矩阵 非对角线上的元素也很有趣。有一些元素并不为零。我们先不关心它们的值(尽管它们具有丰富的信息)。我们只关心矩阵 的非对角线上具有非零值这一事实,这意味着矩阵具有有趣的特征向量。易知它是一个秩为 的矩阵,因此具有两个特征向量。它们是,

确实很有趣!这些特征向量元素的平方定义了后缀集 的条件概率分布。例如,第一个特征向量在 上定义了位串前缀为 的条件概率分布。具体来说: 给定 是位串 的前缀,那么后缀 为 的概率为 ,后缀为 的概率将为 ,后缀分别为 和 的概率值均为 。这是包含在第一个特征向量元素中的信息。第二个特征向量则定义了前缀为 时 的条件概率分布。
特征向量中包含的信息恰好是按传统方式计算边缘概率时丢失的信息。
不过这还不完整!我们仅用 的转置左乘 。如果改变顺序,将看到 矩阵 的对角线元素对应前缀 集上的边缘分布,且其特征向量元素的平方定义了 上的条件概率。
因此矩阵 的对角线具有 的边缘分布。非对角线上的非零元素的存在暗示其特征向量包含条件概率的信息; 则包含了 的相应信息。这两个矩阵加在一起,从原始联合分布中恢复了所有信息,这是用传统方法边缘化时无法做到的。
感觉非常棒吧!但是,数学上到底是怎么回事呢?
. 03 .下期更精彩
矩阵 和 是边缘概率分布的量子版本。
这是什么意思呢?等我下一篇里再讲吧。这里先透露一点:
量子版本的一个概率分布称为密度算子。而量子版本的边缘化对应于将该算子约简到一个子系统。这种约简也是线性代数中的一个概念,称为偏迹。在这个短文系列的下一篇[2]中,我首先会解释偏迹,然后再解释量子版本的含义。在此过程中,我们将展开介绍量子概率论的基础知识。让我们期待吧!
这个短文系列是基于我最近在史密斯学院,CUNY 研究生中心和 Pomona 学院 EDGE/PRiME 座谈会上作的演讲整理而得的。
在 2015 年创办 Math3ma 时,我就希望这个网站的某些方面能反映出我对物理学时时存在的崇敬之心。这也是这个网站的徽标 M 被小电子包围的原因。四年后,我很高兴,终于写了有关数学物理的文章。
衷心感谢 John Terilla 对于本系列短文给予的启发和反馈。
参考文献
[1]二分图: https://www.math3ma.com/blog/matrices-probability-graphs
[2]下一篇: https://www.math3ma.com/blog/a-first-look-at-quantum-probability-part-2
相关阅读
手把手教你将矩阵&概率画成图
手把手教你将矩阵画成张量网络图
看不懂量子?几张萌图揭秘张量积
 点“在看”,分享给朋友吧!
点“在看”,分享给朋友吧!
