点乘和叉乘的数学几何定义

点乘

对于向量a和b而言，向量a=[a1,a2,a3,a4……]，向量b=[b1,b2,b3,b4……]，所以点乘ab=a1b1+a2b2+a3b3+a4b4+……
而在几何定义上：ab=|a||b|cos(theta)——theta代表数学几何里面的向量夹角，所以可得theta=arc cos(a*b/|a||b|)

叉乘

叉乘又称叉积、外积、向量积，两个向量叉乘出来的是一个向量，而这个向量是这两个向量相交所产生的二维平面的法向量，即这个向量与两个相交向量垂直。
假设向量a=[x1,y1,z1]，向量b=[x2,y2,z2]，则向量a向量b的叉乘为：aXb=(y1z2-y2z1)i-(x1z2-x2z1)j+(x1y2-x2y1)k
其中i=(1,0,0),j=(0,1,0),k=(0,0,1)
所以c=aXb=( y1z2-y2z1, -(x1z2-x2z1), x1y2-x2y1 )，几何定义|c|=|a||b|sin(theta)，所以theta=arc sin(|c|/|a||b|)

Unity中的点乘和叉乘

点乘：Vector3.Dot(Vector3 a,Vector3b)
叉乘：Vector3.Cross(Vector3 a,Vector3 b)
代码示例：

//点乘与叉乘的应用
        Vector3 a = new Vector3(1, 2, 3);
        Vector3 b = new Vector3(4, 5, 6);
        //点乘
        float c = Vector3.Dot(a, b);
        //叉乘
        Vector3 d = Vector3.Cross(a, b);
        Vector3 e = Vector3.Cross(b, a);
        //根据点乘和叉乘求a,b之间的角度
        float f = Mathf.Acos(Vector3.Dot(a.normalized, b.normalized)) * Mathf.Rad2Deg;
        float g = Mathf.Asin(Vector3.Distance(Vector3.zero, Vector3.Cross(a.normalized, b.normalized))) * Mathf.Rad2Deg;

        //输出结果
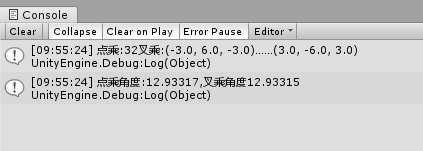
        Debug.Log("点乘:" + c + "叉乘:" + d + "……" + e);
        Debug.Log(string.Format("点乘角度:{0},叉乘角度{1}", f, g));

得出的结果是：

Vector3.normalized代表将这个向量单位化，也就是让这个向量的模长变为1
Vector3.Distance代表两个向量之间的距离
Vector3.zero代表（0,0,0）点
Mathf.Rad2Deg弧长转变成角度，Mathf.Deg2Rad角度转变成弧长