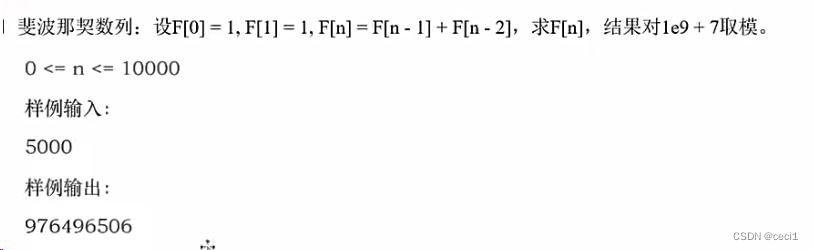一.dfs初印象
dfs是一种常用于图和树的遍历算法,用于遍历所有节点。要想掌握好dfs前提得理解递归的思想。dfs可以理解为一条路走到黑,不行,就返回,接着往下走。
二.dfs模板
基本思路分析:个人觉得重点是找到递归重复的部分,即找到题目中重复需要执行的部分,然后是递归出口的判断;再然后进行回溯,剪枝,记忆化搜索等优化。
def dfs(depth):
#depth为当层第几重循环即深度
if depth==N:
#当到达边界是,即返回
return
#每重循环进行枚举选择,即dfs递归处三.优化
3.1 回溯
回溯就是在搜索尝试过程中寻找问题的解,当发现不满足条件时,就回溯,尝试别的路径。
强调的是此路不通,另寻他路。先打标记,记录路径;然后下一层,回到上一层,清除标记
3.1.1回溯法求全排列
def dfs(depth):
#depth表示当前层数,即已选的个数
if depth==n:
#输出每次的全排列
print(path)
return
for i in range(1,n+1):
#已标记
if vis[i]:
continue
#未标记
vis[i]=1
path.append(i)
#递归下一层
dfs(depth+1)
#回溯
#修改标记
vis[i]=0
#将该数字弹出
path.pop(-1)
n=int(input())
#标记数组,1为标记,0为未标记
vis=[0]*(n+1)
#路径数组
path=[]
dfs(0)3.1.2回溯法解决n皇后问题
import os
import sys
input=sys.stdin.readline
ans=0
#思路:遍历每一行,即遍历的深度,然后在每列中选择合适的位置
def dfs(x):
#出口
if x==n+1:
global ans
ans+=1
#第x层枚举每一列
for y in range(1,n+1):
#如果当前列,主对角线,副对角线已标记
if vis1[y] or visa[x+y] or visb[x-y+n]:
continue
#如果没有标记,先标记,再递归下一行(此时是合法的点)
vis1[y] =visa[x+y] = visb[x-y+n]=True
#递归下一行
dfs(x+1)
#返回上一行,取消标记
vis1[y] =visa[x+y] = visb[x-y+n]=False
n=int(input())
#标记数组
#列
vis1=[False]*(n+1)
#主对角线
visa=[False]*(2*n+1)
#副对角线
visb=[False]*(2*n+1)
#从1开始
dfs(1)
print(ans)
3.2剪枝
主要可分为可行性剪枝和最优化剪枝。可行性剪枝:当前状态和题意不符,并且往后的所有情况和题意都不符,那么就可以剪枝。最优化剪枝:在搜索过程中,当前状态已经不如已经找到的最优解,也可剪枝,不需要继续搜索。
3.2.1剪枝解决数字王国之军训排队
思路:
- dfs搜索,枚举每个学生分到每个组内
- 可行性剪枝:要满足题目条件
- 最优性剪枝:判断当前状态是否比ans更劣
import os
import sys
input=sys.stdin.readline
#倍数关系判断
#判断该学生是否放进当前分组
def check(now_group,y):
#遍历当前组中的元素
for i in now_group:
#是倍数关系
if i%y==0 or y%i==0:
return False
return True
def dfs(depth):
#depth表示当前第几个学生
#最优化剪枝(因为队数不能超过学生数)
global ans
if len(groups)>ans:
return
#递归出口
if depth==n:
ans=min(ans,len(groups))
return
#对于每个学生,枚举放在哪一组
for now_group in groups:
#now_group表示当前组
#可行性剪枝
if check(now_group,a[depth]):
#放入
now_group.append(a[depth])
dfs(depth+1)
now_group.pop()
#直接另做一组
groups.append([a[depth]])
dfs(depth+1)
groups.pop()
n=int(input())
a=list(map(int,input().split()))
#分的队数,相当与一个二维数组
groups=[]
ans=n
dfs(0)
print(ans)
3.2.2 剪枝解决特殊的多边形

import os
import sys
input=sys.stdin.readline
#dfs求所有的n边形,边长乘积不超过100000
def dfs(depth,last_val,tot,mul):
#depth 第depth边,last_val指上一条边长,tot即边长之和,mul即边长之积
#递归出口
if depth==n:
#可行性剪枝
#满足n边形基本定义
#最小的n-1边之和大于第n边 tot-path[-1]>path[-1]
if tot>2*path[-1]:
#合法的n边形
ans[mul]+=1
return
#枚举第depth条边的边长为i
for i in range(last_val+1,100000):
#最优化剪枝
#先前选择了depth个数字,乘积为mul
#后续还有n-depth个数字,每个数字都要>i
if mul*(i**(n-depth))<=100000:
path.append(i)
dfs(depth+1,i,tot+i,mul*i)
path.pop()
else:
break
t,n=map(int,input().split())
#ans[i]表示价值为i的n边形
ans=[0]*100001
path=[]
dfs(0,0,0,1)
#每次询问一个区间l,r,输出多少个n边形的价值在[l,r]中
#等价于ans[l]+....+ans[r],需要对ans求前缀和
for i in range(100001):
ans[i]+=ans[i-1]
for _ in range(t):
l,r=map(int,input().split())
print(ans[r]-ans[l-1])
3.3记忆化搜索
通过记录已经遍历过的状态的信息,从而避免对同一状态重复遍历的搜索实现方式
#记忆化,直接加导这个包即可
from functools import lru_cache
#把普通化递归变成记忆化递归
@lru_cache(maxsize=None)3.3.1记忆化解决斐波那契数列
#记忆化,直接加导这个包即可
from functools import lru_cache
#把普通化递归变成记忆化递归
@lru_cache(maxsize=None)
def f(x):
if x==0 or x==1:
return 1
return f(x-1)+f(x-2)
3.3.2记忆化解决混沌之地


import sys
input=sys.stdin.readline
from functools import lru_cache
@lru_cache(maxsize=None)
def dfs(x,y,z):
#x当前横坐标,y当前纵坐标,z有无使用背包
#出口
if x==C and y==D:
return True
#未抵达出口,往四个方向走
for dx,dy in [(0,1),(0,-1),(1,0),(-1,0)]:
xx,yy=dx+x,dy+y
#边界判断
if xx<0 or xx>=n or yy<0 or yy>=m:
continue
#新位置高度低于当前位置
if a[xx][yy]<a[x][y]:
#直接走
if dfs(xx,yy,z):
return True
#新位置高度高于当前位置,且相差小于k,用掉背包
if a[xx][yy]-a[x][y]<k and z==False:
if dfs(xx,yy,True):
return True
return False
n,m,k=map(int,input().split())
A,B,C,D=map(int,input().split())
A,B,C,D=A-1,B-1,C-1,D-1
a=[]
for i in range(n):
a.append(list(map(int,input().split())))
if dfs(A,B,False):
print("Yes")
else:
print("No")