二叉树的四种遍历方式以及必备的面试题
文章目录
前言
本文介绍二叉树前序遍历、中序遍历、后序遍历、层序遍历以及各自相关的面试OJ题的讲解!
一、构建一个二叉树
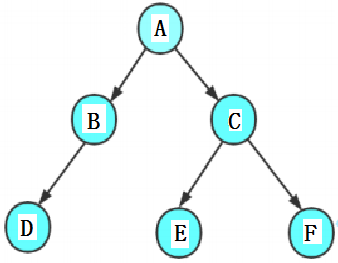
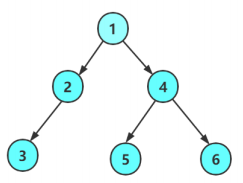
构建如图所示的二叉树,在这里不做过多介绍,想了解怎么构建的可以参考之前的博客!
代码如下(示例):
typedef char BTDataType;
typedef struct BinaryTreeNode
{
struct BinaryTreeNode* left;
struct BinaryTreeNode* right;
BTDataType data;
}BTNode;
BTNode* BuyNode(BTDataType x)
{
BTNode* node = (BTNode*)malloc(sizeof(BTNode));
if (node == NULL)
{
printf("malloc fail\n");
exit(-1);
}
node->data = x;
node->left = node->right = NULL;
return node;
}
BTNode* CreatBinaryTree()
{
BTNode* nodeA = BuyNode('A');
BTNode* nodeB = BuyNode('B');
BTNode* nodeC = BuyNode('C');
BTNode* nodeD = BuyNode('D');
BTNode* nodeE = BuyNode('E');
BTNode* nodeF = BuyNode('F');
nodeA->left = nodeB;
nodeA->right = nodeC;
nodeB->left = nodeD;
nodeC->left = nodeE;
nodeC->right = nodeF;
return nodeA;
}
二、四种遍历方式
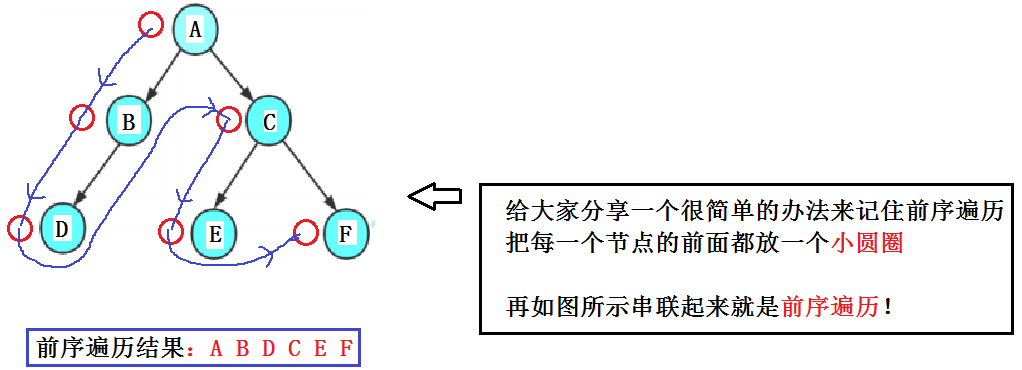
1.前序遍历
前序遍历的顺序为 根 —> 左子树 —> 右子树,下面给大家介绍一种简便方法
代码如下(示例):
// 二叉树前序遍历
void PreOrder(BTNode* root)
{
if (root == NULL) {
printf("NULL ");
return;
}
printf("%c ", root->data);
PreOrder(root->left);
PreOrder(root->right);
}
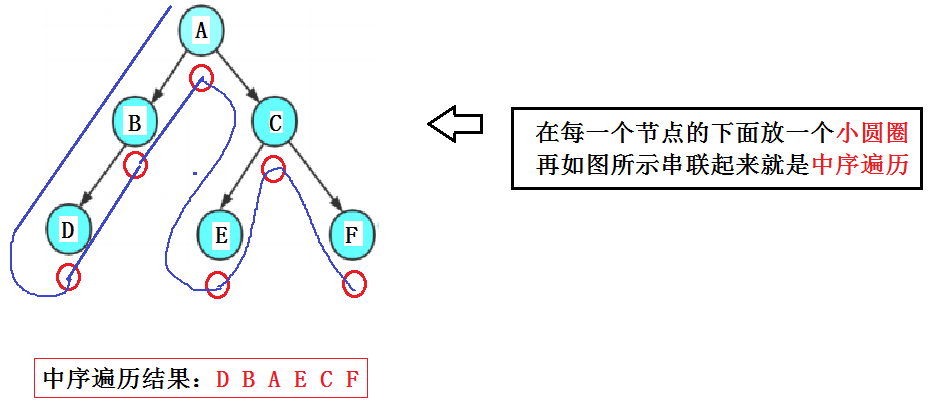
2.中序遍历
中序遍历的顺序为 左子树 —> 根 —> 右子树。
代码如下(示例):
// 二叉树中序遍历
void InOrder(BTNode* root)
{
if (root == NULL) {
printf("NULL ");
return;
}
InOrder(root->left);
printf("%C ", root->data);
InOrder(root->right);
}
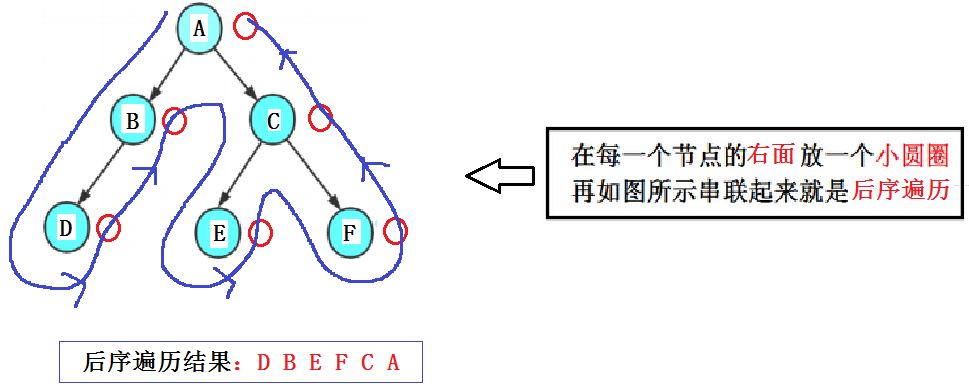
3.后序遍历
后序遍历的顺序为 左子树 —> 右子树 —> 根。
代码如下(示例):
// 二叉树后序遍历
void PostOrder(BTNode* root)
{
if (root == NULL)
{
printf("NULL ");
return;
}
PostOrder(root->left);
PostOrder(root->right);
printf("%C ", root->data);
}
附加: 前三种遍历对比图
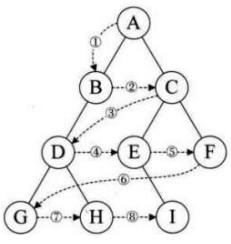
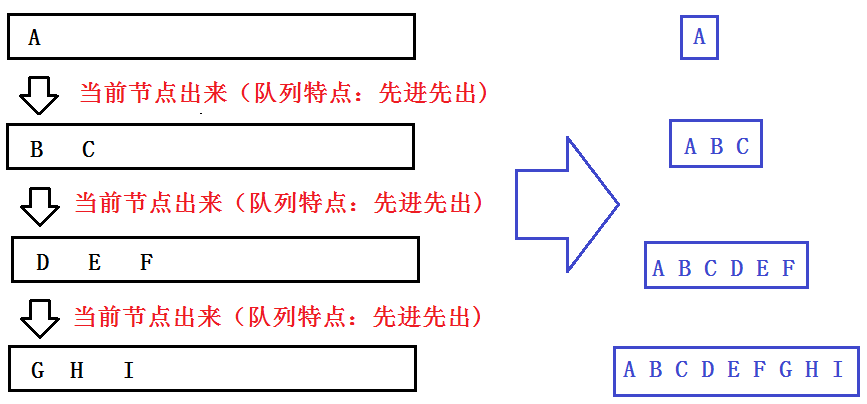
4.层序遍历
层序遍历就是一层一层地遍历,如下图+源码!
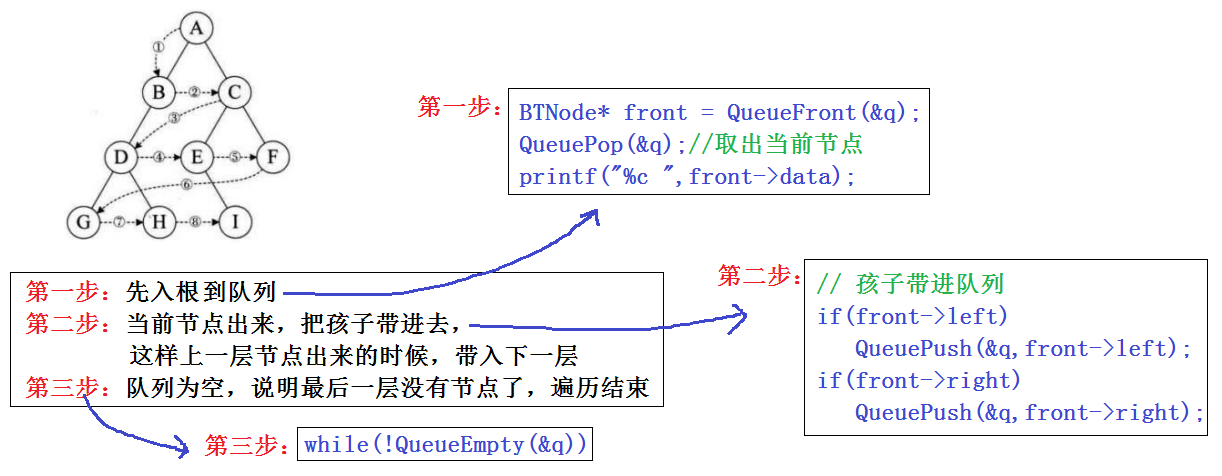
这里我们用队列来实现层序遍历,如下图思路!由于这里会遇到大量队列知识,可以参考:队列实现
代码如下(示例):
// 层序遍历
void BinaryTreeLevelOrder(BTNode* root)
{
if (root == NULL)
return;
Queue q;
QueueInit(&q);
QueuePush(&q, root);
while (!QueueEmpty(&q))
{
BTNode* front = QueueFront(&q);
QueuePop(&q);
printf("%c ", front->data);
// 孩子带进队列
if (front->left)
QueuePush(&q, front->left);
if (front->right)
QueuePush(&q, front->right);
}
printf("\n");
QueueDestroy(&q);
}
三、四种遍历相关的面试题
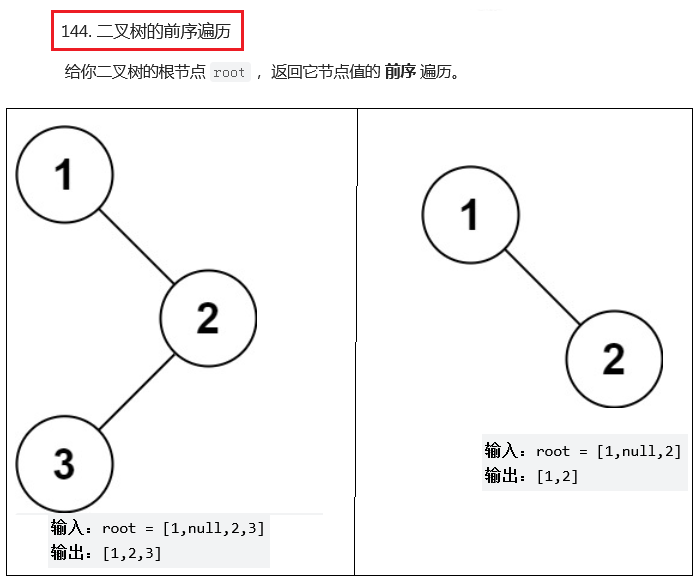
1.第一题:144. 二叉树的前序遍历
(1)题目
题目如下(示例):
int* preorderTraversal(struct TreeNode* root, int* returnSize)
{ }
(2)思路
这里要注意:这道题的返回值为 int* 即要返回一个数组,且*returnSize为数组元素大小
1.size需要自己计算,可以用之前写过的 TreeSize ,不太懂得可以参考 :二叉树节点个数
2.用1子函数来写前序遍历的三步
3.在递归的时候要注意传的是i的地址,因为在传参时,形参是实参的一份临时拷贝,要传&i
4.最后把size 给 *returnSize ,以保证数组大小!
(3)源码
代码如下(示例):
//先求下数组的大小,便于开辟空间
int Treesize(struct TreeNode* root)
{
return root == NULL ? 0 : Treesize(root->left) + Treesize(root->right) + 1 ;
}
void _preorderTraversal(struct TreeNode* root , int* a, int* pi)
{
if(root == NULL)
{
return;
}
a[(*pi)++] = root->val;
_preorderTraversal(root -> left ,a,pi);
_preorderTraversal(root->right , a ,pi);
}
int* preorderTraversal(struct TreeNode* root, int* returnSize)
{
int size = Treesize(root);
int* a = (int*)malloc(sizeof(int)*size);
int i = 0;
_preorderTraversal(root , a , &i);
*returnSize = size;
return a;
}
2.第二题:94. 二叉树的中序遍历
3.第三题:145. 二叉树的后序遍历
第二题和第三题和第一题解法一样,这里不做过多介绍,这里直接给出答案!
第二题答案:如下(示例):
int Treesize(struct TreeNode* root)
{
return root == NULL ? 0 : Treesize(root->left) + Treesize(root->right) + 1 ;
}
void _inorderTraversal(struct TreeNode* root , int* a, int* pi)
{
if(root == NULL)
{
return;
}
_inorderTraversal(root -> left ,a,pi);
a[(*pi)++] = root->val;
_inorderTraversal(root->right , a ,pi);
}
int* inorderTraversal(struct TreeNode* root, int* returnSize)
{
int size = Treesize(root);
int* a = (int*)malloc(sizeof(int)*size);
int i = 0;
_inorderTraversal(root , a , &i);
*returnSize = size;
return a;
}
第三题答案:如下(示例):
int Treesize(struct TreeNode* root)
{
return root == NULL ? 0 : Treesize(root->left) + Treesize(root->right) + 1 ;
}
void _postorderTraversal(struct TreeNode* root , int* a, int* pi)
{
if(root == NULL)
{
return;
}
_postorderTraversal(root -> left ,a,pi);
_postorderTraversal(root->right , a ,pi);
a[(*pi)++] = root->val;
}
int* postorderTraversal(struct TreeNode* root, int* returnSize)
{
int size = Treesize(root);
int* a = (int*)malloc(sizeof(int)*size);
int i = 0;
_postorderTraversal(root , a , &i);
*returnSize = size;
return a;
}
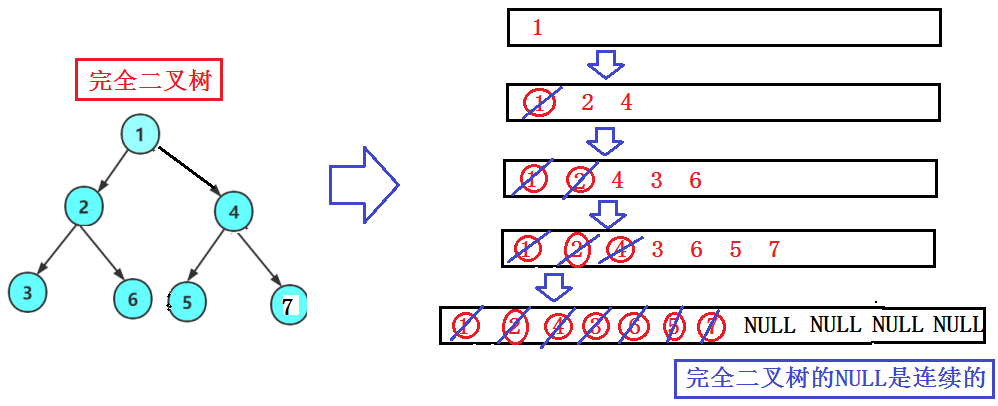
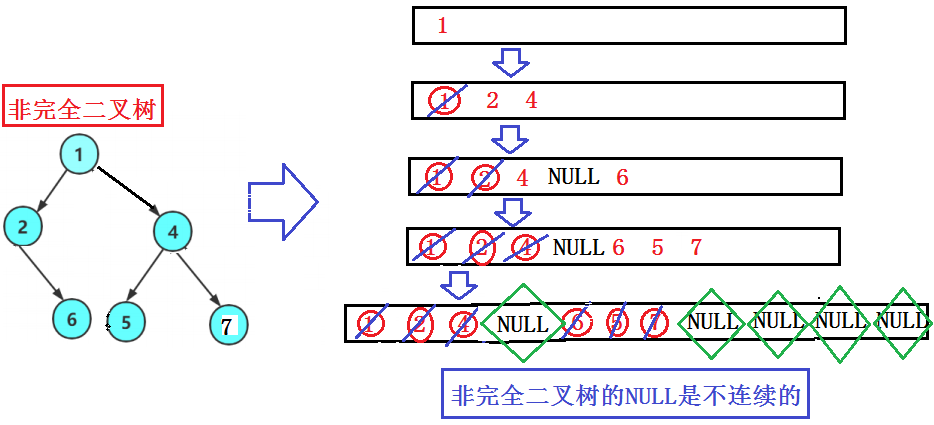
4.第四题:判断二叉树是否是完全二叉树
(1)思路
(2)源码
代码如下(示例):
// 判断二叉树是否是完全二叉树
bool BinaryTreeComplete(BTNode* root)
{
Queue q;
QueueInit(&q);
QueuePush(&q, root);
while (!QueueEmpty(&q))
{
BTNode* front = QueueFront(&q);
QueuePop(&q);
if (front == NULL)
{
break;
}
else
{
QueuePush(&q, front->left);
QueuePush(&q, front->right);
}
}
// 遇到空了以后,检查队列中剩下的节点
// 1、剩下全是空给,则是完全二叉树
// 2、剩下存在非空,则不是完全二叉树
while (!QueueEmpty(&q))
{
BTNode* front = QueueFront(&q);
QueuePop(&q);
if (front)
{
QueueDestroy(&q);
return false;
}
}
QueueDestroy(&q);
return true;
}
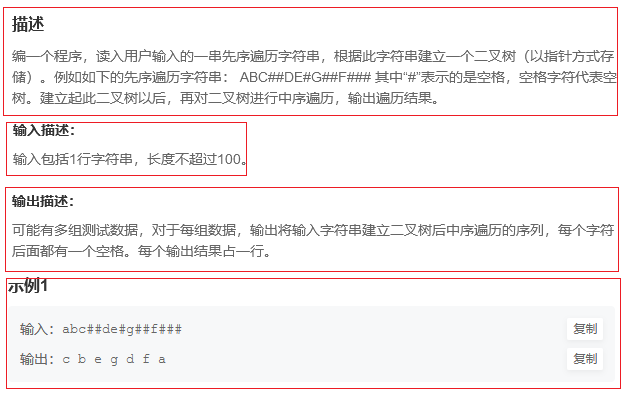
5.第五题:KY11 二叉树遍历
(1)题目
(2)思路
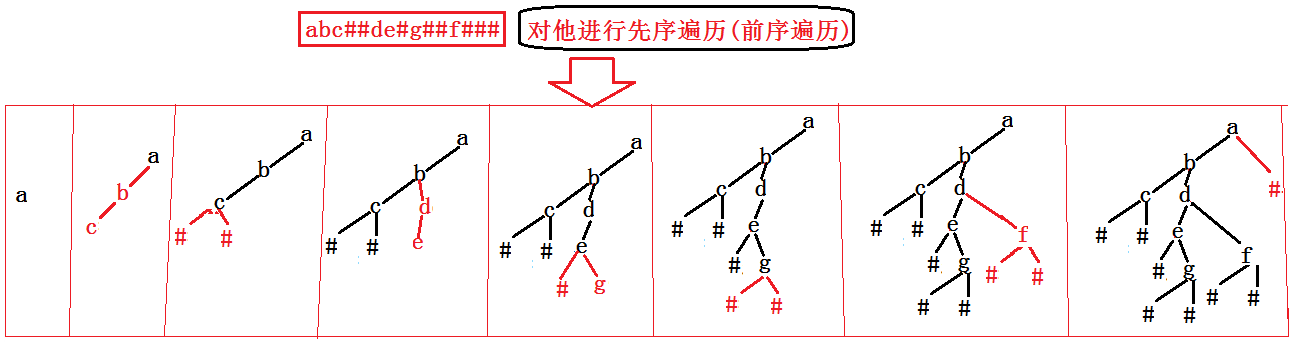
这道题需要分成不同地模块来完成!
1.构建树,用 结构体 TreeNode
2.写中序遍历,不会写的看前面文章!
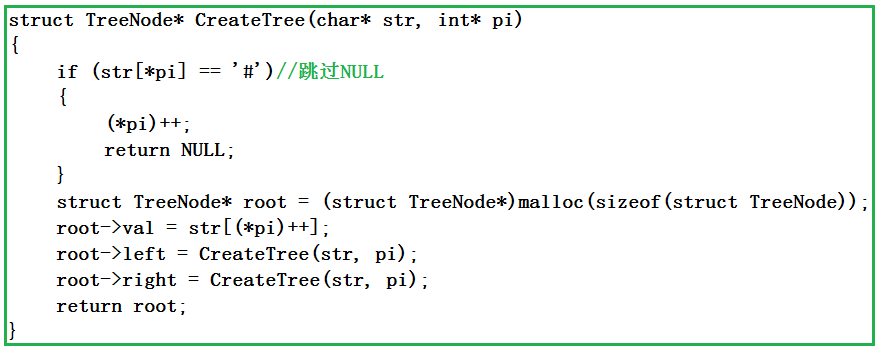
3.如果是 # 就跳过并返回NULL ,如下图所示!
构建完二叉树之后,就可以对每一个节点进行中序遍历并打印,不会中序遍历的可以参考前面!
(3)源码
代码如下(示例):
#include<stdio.h>
#include <stdlib.h>
struct TreeNode {
struct TreeNode* left;
struct TreeNode* right;
char val;
};
struct TreeNode* CreateTree(char* str, int* pi) {
if (str[*pi] == '#') {
(*pi)++;
return NULL;
}
struct TreeNode* root = (struct TreeNode*)malloc(sizeof(struct TreeNode));
root -> val = str[(*pi)++];
root -> left = CreateTree(str, pi);
root -> right = CreateTree(str, pi);
return root;
}
void InOrder(struct TreeNode* root) {
if (root == NULL)
return;
InOrder(root->left);
printf("%c ", root->val);
InOrder(root->right);
}
int main() {
char str[100];
while ((scanf("%s", str) != EOF)) {
int i = 0;
struct TreeNode* root = CreateTree(str, &i);
InOrder(root);
}
return 0;
}
最后:销毁二叉树
在我们每次创建完二叉树之后要销毁二叉树,否则会导致内存泄漏!
(1)源码
代码如下(示例):
void BinaryTreeDestory(BTNode* root)
{
if (root == NULL)
{
return;
}
BinaryTreeDestory(root->left);
BinaryTreeDestory(root->right);
free(root);
}
(2)递归图解
想销毁如图所示的二叉树!为了方便我只画了一条路径上的销毁递归图,感兴趣的可以都画!
总结
以上就是今天要讲的内容,本文介绍二叉树的四种遍历方式以及必备的面试题。
如果我的博客对你有所帮助记得三连支持一下,感谢大家的支持!