快速排序————非递归实现

二.递归实现快速排序

2.1.为什么我们要去通过递归实现我们的快速排序呢？

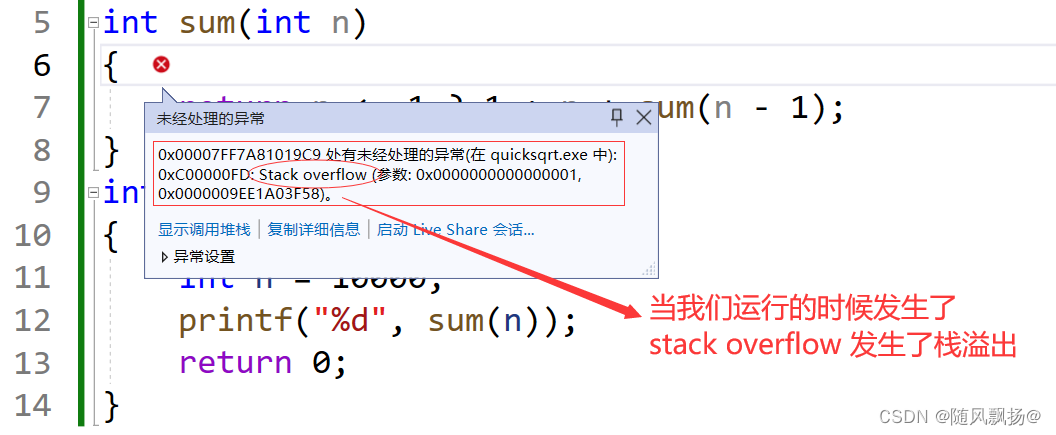
大家有可能会想是不是因为递归非常的占用空间，我们都知道我们的局部变量是保存在栈上的我们的函数参数也是在栈上开辟的，所以说递归是不是会占用我们非常多的栈空间，同时呢我们的递归是一个非常深的一个操作，我们往往会因为一个函数递归出来的结果而去让这个函数重复调用多次去解决我们当前的问题，我们的快速排序非递归就是这样的方式，也包括之前的一个斐波那契数列使用递归去解决都是使用了栈；这样的方法在递归的深度不大的时候不会产生什么问题但是如果我们需要去处理的数据非常多，递归的深度非常深那么我们这个时候递归真的不会出现问题吗？

举一个例子：

我们去使用递归求1+2+3+4+。。。。n；

我们从n=100 n=1000 n=1000; 来看一看会是什么样的结果

由此可见在一些数据过大的情况下我们的递归是非常非常难进行下去的，首先他的数据越多我们的递归越深，栈的空间就越来越少，最后入不敷出我们的栈就溢出了（stack over）；

现在就知道我们为什么要使用我们的的非递归来为此我们的快速排序！

2.2，使用非递归实现我们的快速排序

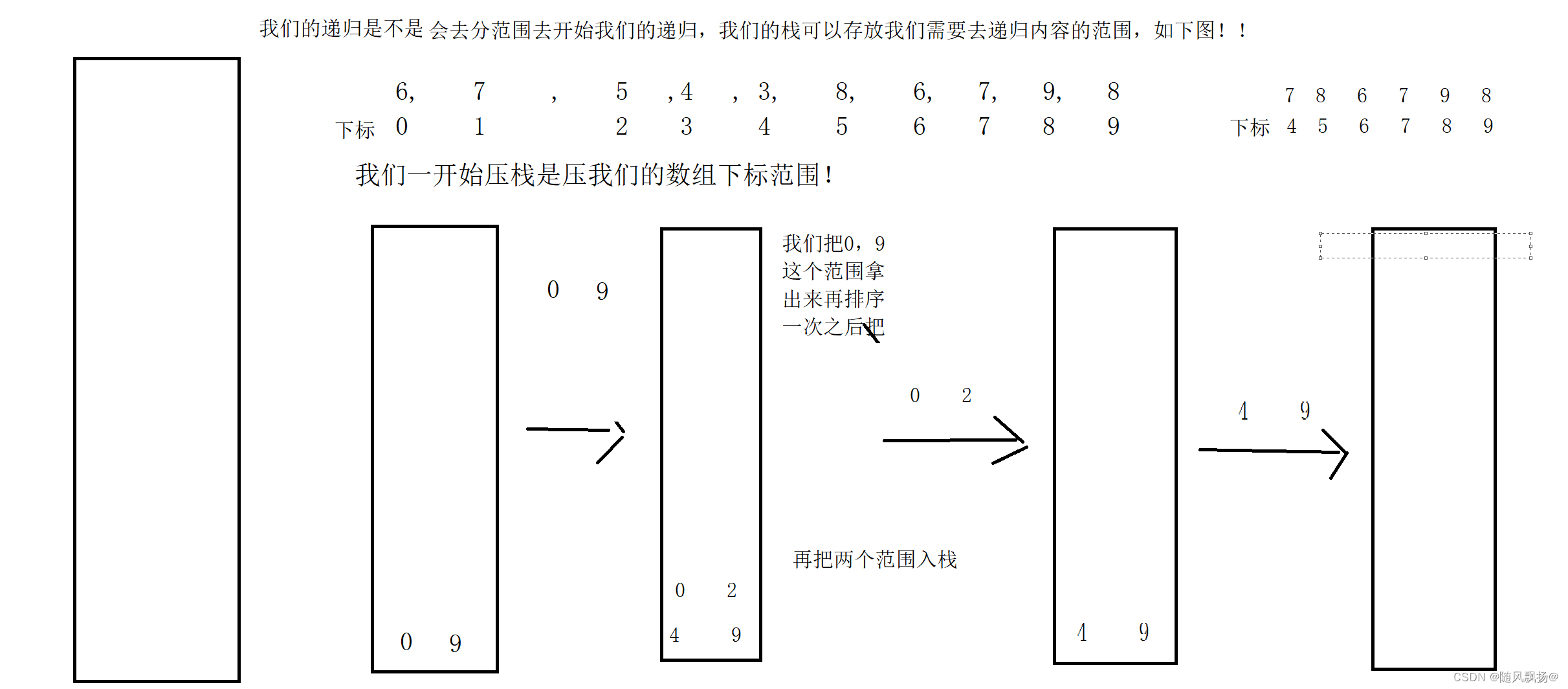
我们可以先通过递归的特点来想一想如何通过栈去转换？

1.初始化我们的栈。

2.入栈把我们的开始的left==0 right==n-1；

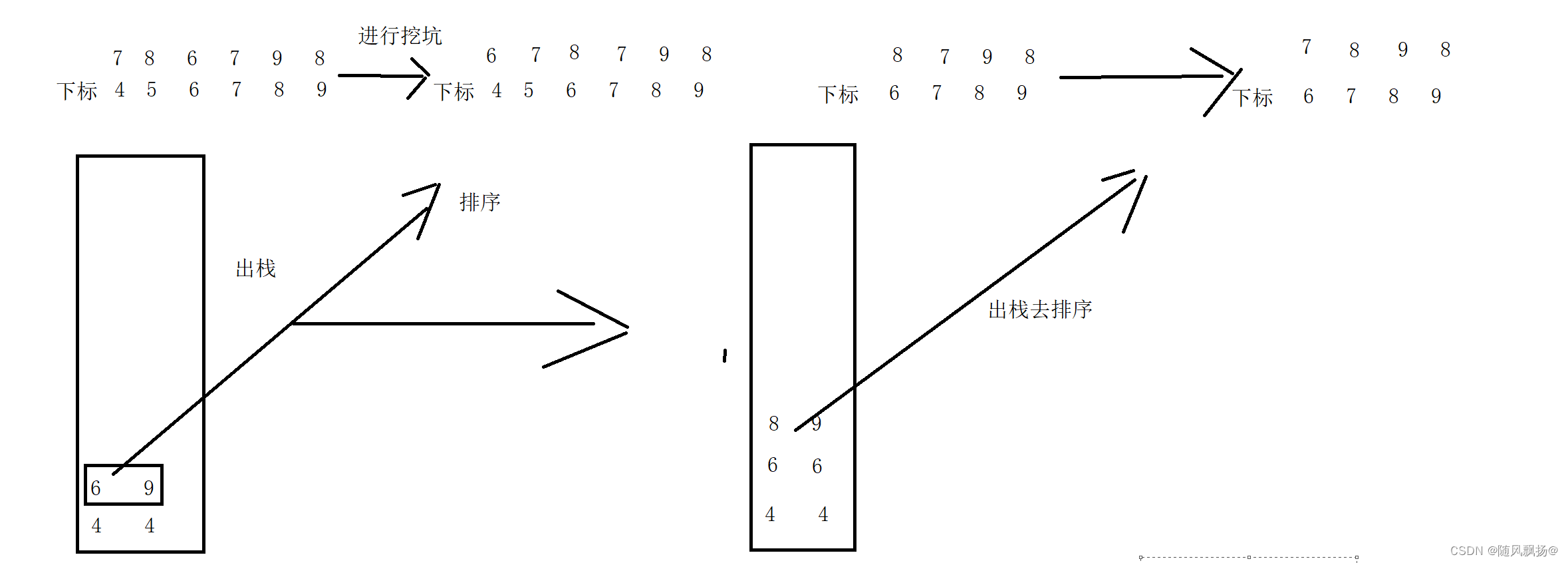
3.进入我们的循环体循环体进入的条件是判断栈中是否还有数值如果有数值的化什么其中的数值对应的范围还是没有序的就需要出栈（这个时候就需要进行出栈（注意栈的数值的左右范围的对应））进行我们的挖坑排序（对于挖坑我们应该把key返回出来通过key的数值进行我们再一次的入栈操作同时我们的范围）。

3.1[left key-1] 和[key+1 right] 这样的范围满足条件才能继续push 之后pop进行我们的排序；

4如果说我们的循环体结束了的话我们的数组就一定有序！

（这里需要注意的是入栈和出栈的对应的left 和 right 不要拿错了这个时候可以自己画一画图看一看，并且当我们的范围小到自己和自己是不是就不需要push入栈去进行自己和自己的排序所以这个地方push的条件也非常重要！）

//栈的声明
#pragma once

#include<stdio.h>
#include<stdbool.h>
#include<assert.h>
#include<stdlib.h>

typedef int STDataType;

typedef struct strck
{
	STDataType* a;//数据
	int top;//栈顶
	int capacity;//容量
}ST;

//实现的的功能
//传地址才能改变
// 
//进行一个初始化
void StackInit(ST* ps);
//进行内容释放
void StackDestory(ST* ps);
//进行入数据,栈只规定在顶去push；
void StackPush(ST* ps, STDataType x);
//进行出数据，栈只规定在定去pop
void StackPop(ST* ps);
//获取栈顶的数据
STDataType StackTop(ST* ps);
//获取栈的大小
int Stacksize(ST* ps);
//判断栈是否为空
bool StackEmpty(ST* ps);

#include"strack.h"

//进行一个初始化
void StackInit(ST* ps)
{
	ps->a = (STDataType*)malloc(sizeof(STDataType) * 4);
	if (ps->a == NULL)//开辟空间失败
	{
		printf("realloc fail\]n");
		exit(-1);
	}
	
		ps->top = -1;
	    //ps->top = -1;
		//ps->top=0;
		ps->capacity = 4;
	
}

//进行内容释放
void StackDestory(ST* ps)
{
	assert(ps);//断言只有不是空才可以被释放
	free(ps->a);
	ps->a = NULL;
	ps->capacity = 0;
	ps->top = 0;
}
//进行入数据,栈只规定在顶去push；
void StackPush(ST* ps, STDataType x)
{
	//我们的栈top==-1开始我们要++再入数据
	assert(ps);//进行判断

	//进行加空间
	if (((ps->top)+1) == (ps->capacity))//top+1 不这样的化容量是认为我们是够的但是-1，开始实际上是不够的；
	{
		STDataType* tmp = (STDataType*)realloc(ps->a,
			sizeof(STDataType) * 2*ps->capacity);
		if (tmp == NULL)//开辟空间失败
		{
			printf("realloc fail\]n");
			exit(-1);
		}
		else//开辟空间成功
		{
			ps->capacity *= 2;
			ps->a = tmp;
		} 
	}
	ps->top++;
	ps->a[ps->top] = x;
	//(ps->top)++;
	//*(ps->a + (ps->top)) = x;另一种方法


}


//进行出数据，栈只规定在定去pop
void StackPop(ST* ps)
{
	assert(ps);
	assert(ps->top >= -1);
	//assert(ps->top > 0);
	//加一个条件不敢去一直--；
	ps->top--;

}
//获取栈顶的数据
STDataType StackTop(ST* ps)
{
	assert(ps);
	//assert(ps->top >= -1);
	return ps->a[ps->top];//我们的top从-1开始所以
	return ps->a[ps->top-1];

}
//获取栈的大小
int Stacksize(ST* ps)
{
	return (ps->top + 1);
	//return ps->top ;
}
//判断栈是否为空
bool StackEmpty(ST* ps)
{
	assert(ps);
	return (ps->top == -1);
	//return (ps->top == 0);
}

有一说一这个非递归实现快速排序是非常有意义他考察了我们对于栈的实现和应用能力，加入了我们快速排序的特点，这个题目的挖坑排序返回值是非常重要的，同时对于改变环境下的关于在对应情况下的是否入栈也十分重要！！！希望这篇文章可以帮助到大家！！！