目录
前言
说起二分查找,也是一种十分常见的算法,最常听说的就是:二分查找只能在数组有序的场景下使用;其实也未必,只要能找到规律,也依然可以使用;本文我将分享一些有关二分查找算法的做题经验;
1. 二分查找(基础版)
注意:二分查找算法也并非是只能在数组有序的场景下使用,只要数据具有 " 二段性 " 就可以使用;
基础版的二分查找,没有那么多弯弯绕绕,以及边界情况;下面是一个基础版本的示例:
while( left <= right)
{
int mid = left + (right - left) / 2;
if(nums[mid] > target) right = mid - 1;
else if(nums[mid] < target) left = mid + 1;
else return mid;
}在计算中间点时比较推荐示例中的写法:
int mid = left + (right - left) / 2;这种方式可以有效的防止数据溢出;
由此可以总结出基础版本的二分模板:
while( left <= right)
{
int mid = left + (right - left) / 2;
if(...)
right = mid -1;
else if(...)
left = mid + 1;
else
return ...;
}2. 寻找左右端点
这种方式的二分算法有比较经典的题目:
力扣中的第34道题:
这种类型再使用基础版本的二分就没法很好的解决:
使用基础版本只能找到一组目标值中的某一个,比如:
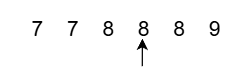
nums = [5,7,8,8,8,9]; // target = 8基础版本只能保证找到数组中的8(目标值),但是要知道目标值开始位置和解释位置就不行了;还需要进行一些操作,但这样就容易让时间复杂度降到 O(N),也就是所有值都是目标值的情况;因此基础版本在这道题中并不是最优解;这时就可以使用二分的进阶版:寻找区间左右端点;
怎么找左右端点?
还是使用这个示例:
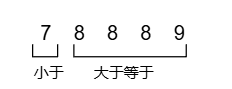
nums = [5,7,8,8,8,9];寻找端点版本,主要分成两种情况(设中间点为x):
以寻找左端点为例(以下的示例都是以求左端点):
- x < target:left = mid + 1;在区间[left,right]中找;
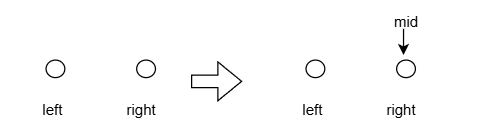
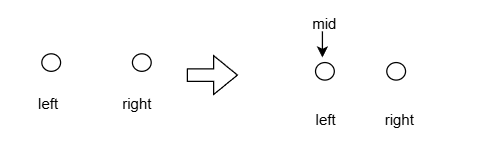
- x >= target:right = mid;
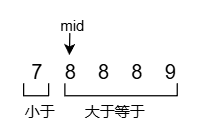
将数组划分成两个区间;right为什么是等于mid就一目了然了;
当mid在如图的位置时,如果right = mid + 1;那么剩下的区间就不会有target;
较为难的点就是细节的处理,这里很容易出错,一旦出错就会成死循环;
细节:求中间点、循环条件
循环判断条件
判断条件是:
while(left < right){
...
}不需要判断是否相等,如果判断了就会死循环;
- x < target:left = mid + 1;
- x >= target:right = mid;
比如:
如果right == left时还进入循环判断,此时走的是 x >= target;right还是会在原来的位置;这样就会造成死循环;
求中间点
求中间点有两种:
// 第一种
mid = left + (right - left) / 2;
// 第二种
mid = left + (right - left + 1) / 2;他们的区别在于当数组元素为偶数的时候:
第一种:
第二种:
求左端点只能使用第一种,否则也会造成死循环:
如果是第二种情况:
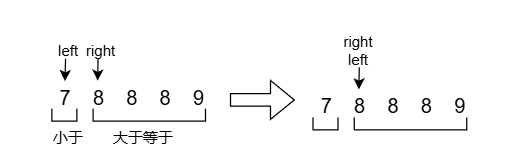
假设区间只剩两个端点:
使用第二种方法计算出的mid是右边的端点;那么当满足 x < target:left = mid + 1;时循环退出;如果满足的是 x >= target:right = mid;就会出现死循环;
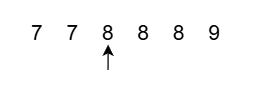
而第一种:
当满足 x < target:left = mid + 1;时 left走到right位置,循环结束;
当满足的是 x >= target:right = mid;right走到mid位置(也就是left位置),循环结束;
总结一下:
// 寻找左端点
while(left < right) {
int mid = left + (right - left) / 2;
if(left < target)
left = mid + 1;
else right = mid;
}
// 寻找右端点
while(left < right) {
int mid = left + (right - left + 1) / 2;
if(right > target)
right = mid - 1;
else left = mid;
}可以得出模板:
// 寻找左端点
while(left < right) {
int mid = left + (right - left) / 2;
if(...)
left = mid + 1;
else right = mid;
}
// 寻找右端点
while(left < right) {
int mid = left + (right - left + 1) / 2;
if(...)
right = mid - 1;
else left = mid;
}提醒:注意本文对二分进行了模板的总结,切记不要一味的记忆模板,要基于理解去使用;
以下是一些题目练习:
总结
以上便是本文的全部内容,希望对你有所帮助,最后感谢阅读!