目录
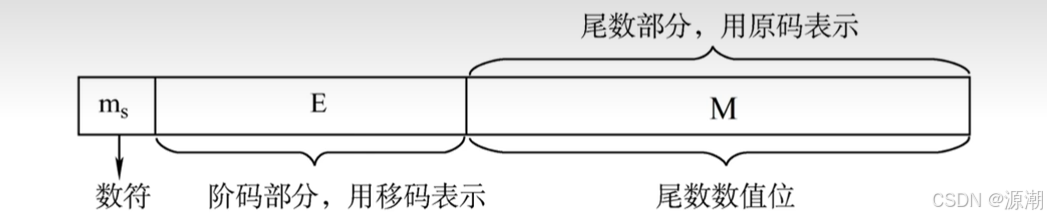
1.基本表示:
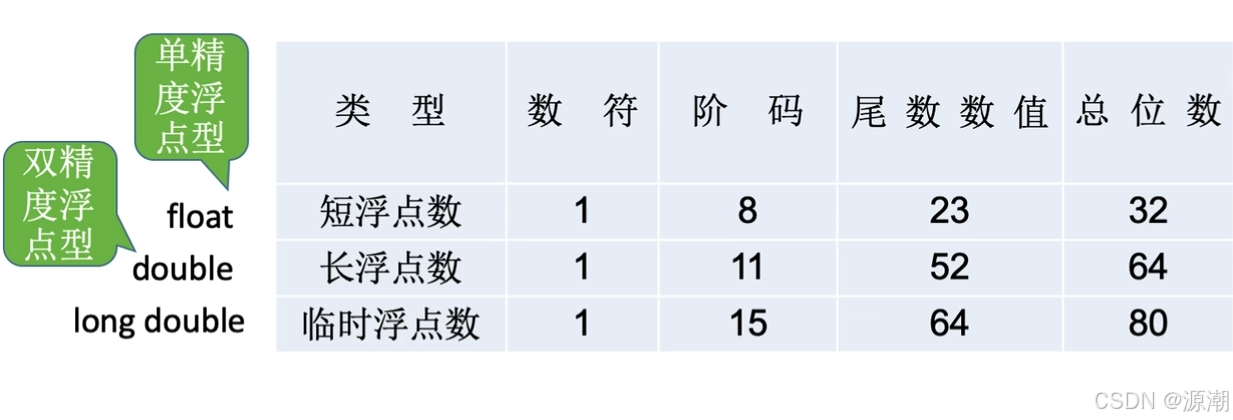
以单精度浮点数float(32位)为例:
数符:正负(正0负1)(1位)
阶码:移码表示(8位)
尾数:以原码表示(23位)
2.基础运算:
例1:将十进制数 -0.75 转化为IEEE 754的单精度浮点数格式表示
1.由于十进制数为负,可以直接确定数符位为 1
2.将十进制数转化为二进制:(0.75)= (0.11)=(1.1)* 2^-1
可知尾数部分为:0.100000.......(末尾添0凑够23位)
3.阶码真值 e = -1 可由E = 127+e 推出E = 126
再用二进制表示E = 01111110(如果不够八位,首位添0凑够八位)
例2:IEEE 754的单精度浮点数 C0 A0 00 00 H的值表示为多少。
先将十六进制转为二进制 :1100 0000 1010 0000 0000 0000 0000 0000
根据各部分占位数进行分割:1 100 0000 1 010 0000 0000 0000 0000 0000
可知数符位为1 为负
阶码:1000 0001为移码表示 转化为补码为 0000 0010 也是原码 真值表示为2
尾数:1.01000000.....
浮点数真值 = (-1.01) * 2^2 = -1.25 * 4 = -5.0
注:移码补码互转为从左往右数第一个1的左侧所有位取反 末尾在加1
2023计算机考研408统考第14题
解析:A若E = 0,且M≠0,则 N = (-1)S×2-126×(0.M)。
8020 0000H = 1000 0000 0010 0000 0000 0000 0000 0000代入公式,(-1)^1 ×(0.01)×2^(-126) = -2^-128
题目解释:第二章节浮点数的表示,真题中常见考点关于浮点数的问题,要不是浮点数表示,要不就是浮点数的运算。今年的这个浮点数考的比较细致,也是比较特殊的一种情况,这里注意E的范围是否为规格化数或者不规格化数从而采取不同的方式处理,有些同学可能并没有在意这个,这是提醒大家考研就是要全面、多次、细致的学习与复习。这一类型在课程的强化与基础时都有强调