💎 欢迎大家互三:2的n次方_
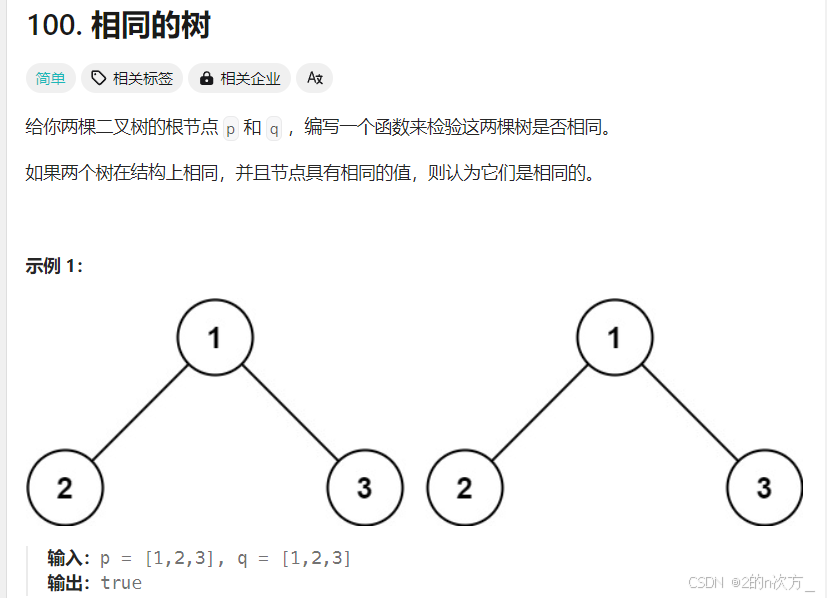
1. 相同的树
同时遍历两棵树
判断结构相同:也就是在遍历的过程中,如果有一个节点为null,另一棵树的节点不为null,那么结构就不相同
判断值相同:只需要在遍历的过程中判断当前节点的val值是否相同
class Solution {
public boolean isSameTree(TreeNode p, TreeNode q) {
//判断结构
if ((p == null && q != null) || (p != null && q == null))
return false;
if (p == null && q == null)
return true;
//判断值
if (p.val != q.val)
return false;
//遍历判断左子树和右子树
return isSameTree(p.left, q.left) && isSameTree(p.right, q.right);
}
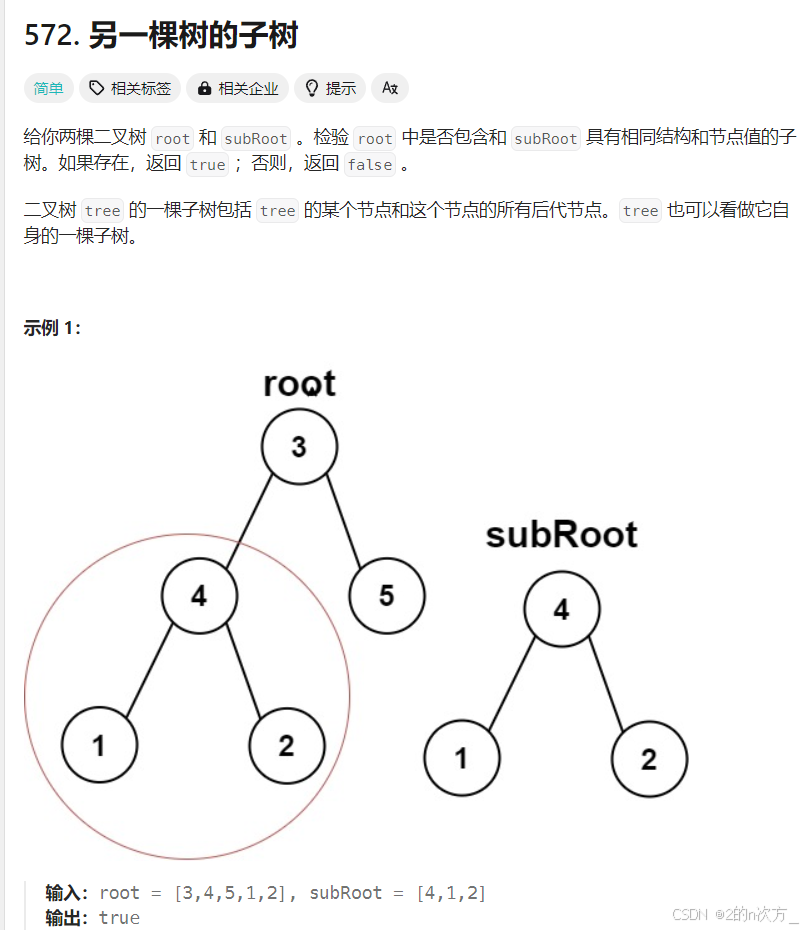
}2. 另一棵树的子树
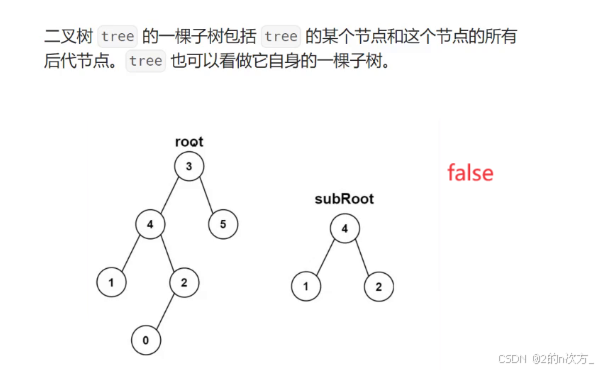
这里给出的子树定义是需要包括某个节点和这个节点所有后代节点,少一个都不行
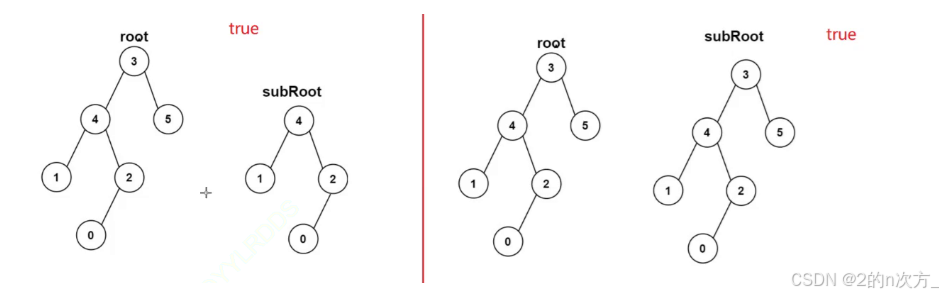
下面这两种就可以看作是子树
思路:
1.判断当前子树是否和根节点一样
2.判断子树是否和当前root的左子树一样
3.判断子树是否和当前root的右子树一样
判断两棵树是否一样在上一题已经写好了,可以直接拿来用
class Solution {
public boolean isSubtree(TreeNode root, TreeNode subRoot) {
if(root == null) return false;
if(isSameTree(root,subRoot)) return true;
if(isSubtree(root.left,subRoot)) return true;
if(isSubtree(root.right,subRoot)) return true;
return false;
}
public boolean isSameTree(TreeNode p, TreeNode q) {
if ((p == null && q != null) || (p != null && q == null))
return false;
if (p == null && q == null)
return true;
if (p.val != q.val)
return false;
return isSameTree(p.left, q.left) && isSameTree(p.right, q.right);
}
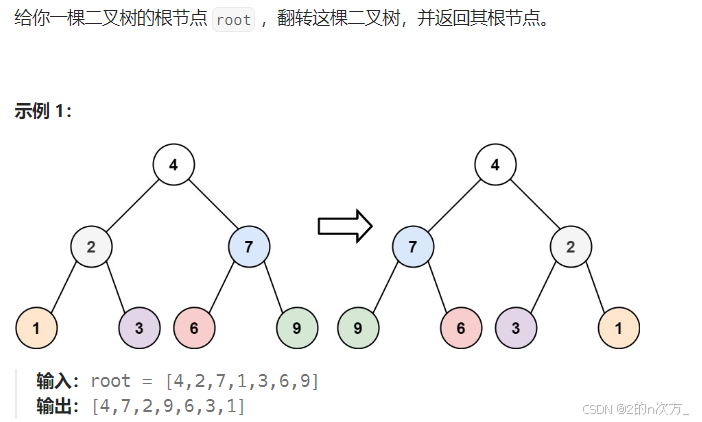
}3. 翻转二叉树
这道题只需要在遍历的同时把当前节点的左子树和右子树进行交换即可
class Solution {
public TreeNode invertTree(TreeNode root) {
if (root == null)
return null;
if (root.right == null && root.left == null)
return root;
TreeNode tmp = root.left;
root.left = root.right;
root.right = tmp;
invertTree(root.left);
invertTree(root.right);
return root;
}
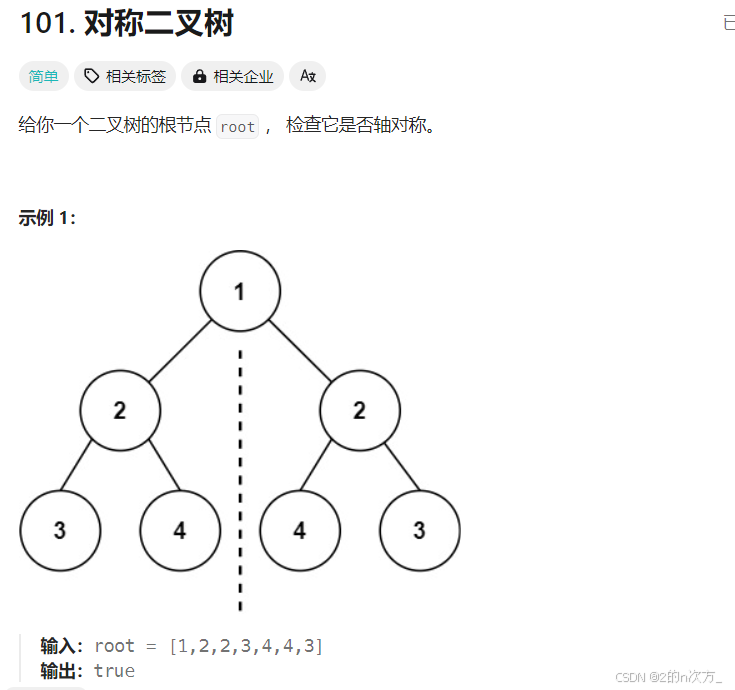
}4. 对称二叉树
思路:对称二叉树其实就是左子树的左子树和右子树的右子树,左子树的右子树和右子树的左子树的值相同,和之前判断相同的树类似,先比较结构,如果结构不一样肯定不是对称的,接着再判断值,通过递归实现左子树和右子树的判断
public boolean isSymmetric(TreeNode root) {
if (root == null)
return true;
return isSymmetricChild(root.left, root.right);
}
public boolean isSymmetricChild(TreeNode root1, TreeNode root2) {
//判断结构相同
if (root1 != null && root2 == null || root1 == null && root2 != null) {
return false;
}
if (root1 == null && root2 == null) {
return true;
}
//判断值相同
if(root1.val != root2.val){
return false;
}
//左子树的左子树和右子树的右子树,左子树的右子树和右子树的左子树
return isSymmetricChild(root1.left,root2.right) && isSymmetricChild(root1.right,root2.left);
}5. 平衡二叉树
平衡二叉树是指任意节点的两个子树的高度差不超过1的二叉树
思路:遍历这棵树的每一个节点,求每一个节点的左子树和右子树,判断高度是否相差大于1,并且左子树和右子树也要是平衡二叉树
class Solution {
public boolean isBalanced(TreeNode root) {
if(root == null) return true;
int res = getHeight(root.left) - getHeight(root.right);
if(res <= -2 || res >= 2){
return false;
}
return isBalanced(root.left)&&isBalanced(root.right);
}
//求树的高度
public int getHeight(TreeNode root) {
if (root == null)
return 0;
int leftHeight = getHeight(root.left);
int rightHeight = getHeight(root.right);
return (leftHeight > rightHeight) ? leftHeight + 1 : rightHeight + 1;
}
}这种方法简单直观,但是时间复杂度是O(n²)的,因为每次判断一个节点时,都要判断一次子树,重复计算,性能不高,接下来优化一下
class Solution {
public boolean isBalanced(TreeNode root) {
if(root == null) return true;
//如果返回-1表示不是平衡二叉树
return getHeight(root) >= 0;
}
public int getHeight(TreeNode root) {
if (root == null)
return 0;
int leftHeight = getHeight(root.left);
//如果拿到的还是-1,表示已经不是平衡二叉树,返回-1
if(leftHeight < 0){
return -1;
}
int rightHeight = getHeight(root.right);
if(rightHeight >= 0 && Math.abs(leftHeight - rightHeight) <= 1){
return Math.max(leftHeight,rightHeight) + 1;
}else{
return -1;
}
}
}上面优化的是如果已经判断出不是平衡二叉树,就返回-1,不用再进行其他判断了
6. KY11 二叉树遍历
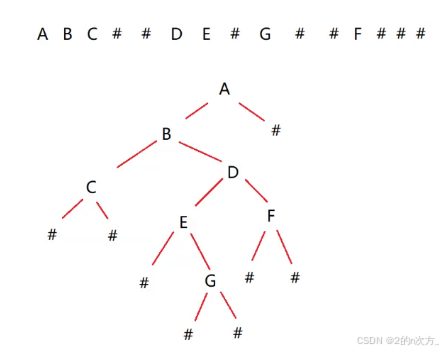
例如,根据题目中输入的字符串可以构建出这样一棵二叉树
那么怎么去实现呢
首先就是遍历字符串,遇到 "#" 就跳过,不是的话就创建相应的节点,并通过递归的形式,进行左右子节点的连接
class TreeNode {
public char val;
public TreeNode left;
public TreeNode right;
public TreeNode(char val) {
this.val = val;
}
}
public class Main {
public static void main(String[] args) {
Main main = new Main();
Scanner in = new Scanner(System.in);
// 注意 hasNext 和 hasNextLine 的区别
while (in.hasNextLine()) { // 注意 while 处理多个 case
String str = in.nextLine();
TreeNode root = main.createTree(str);
main.inOrder(root);
}
}
public int i = 0;
//在递归的过程中连接节点
public TreeNode createTree(String str) {
TreeNode root = null;
if (str.charAt(i) != '#') {
root = new TreeNode(str.charAt(i));
i++;
root.left = createTree(str);
root.right = createTree(str);
} else {
i++;
}
return root;
}
//遍历打印
public void inOrder(TreeNode root) {
if (root == null) return;
inOrder(root.left);
System.out.print(root.val + " ");
inOrder(root.right);
}
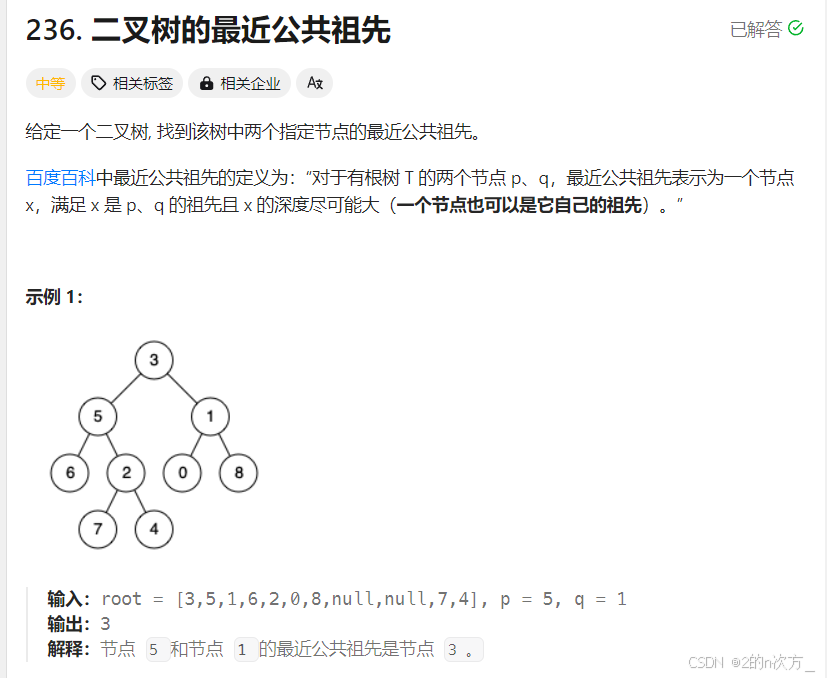
}7. 二叉树的最近公共祖先
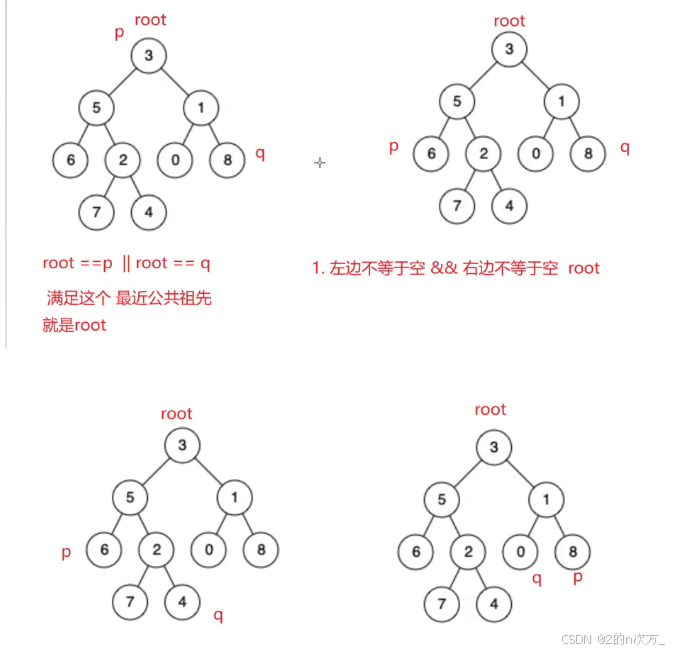
可以分为下面几种情况 :
如果刚开始就是root是p或者q,直接返回root,不是的话就去左右子树里边找,首先就是p,q在两边的情况,那么就是左右子树的返回值都不为空,根节点root就是最近公共祖先,然后就是p,q在同一边的情况,这个又可以分为两种情况,首先就是p,q不在同一深度,此时就又回到了刚开始的情况,新的根节点就是最近公共祖先,然后就是p,q在通一深度的情况,此时,新的root还是最近公共祖先
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if (root == null)
return null;
if (root == p || root == q) {
return root;
}
TreeNode leftNode = lowestCommonAncestor(root.left, p, q);
TreeNode rightNode = lowestCommonAncestor(root.right, p, q);
if(rightNode != null && leftNode != null){
return root;
}else if(leftNode!=null){
return leftNode;
}else{
return rightNode;
}
}
}除了这种方法,还有另外一种思路,可以看作链表的交叉来做