1. 运算符
<<:左移运算符,左边移出的位被丢弃,右边空出的位用 0 填充。
>>:右移运算符,将左边的操作数的二进制表示向右移动右边操作数指定的位数。
~:按位取反,将操作数的二进制表示中的每一位进行取反操作
&:与运算,有 0 结果就是 0
|:或运算,有 1 结果就是 1
^:亦或,相同为 0,相异为 1 / 不进位相加
2. 基本操作
191,338,461,136,260
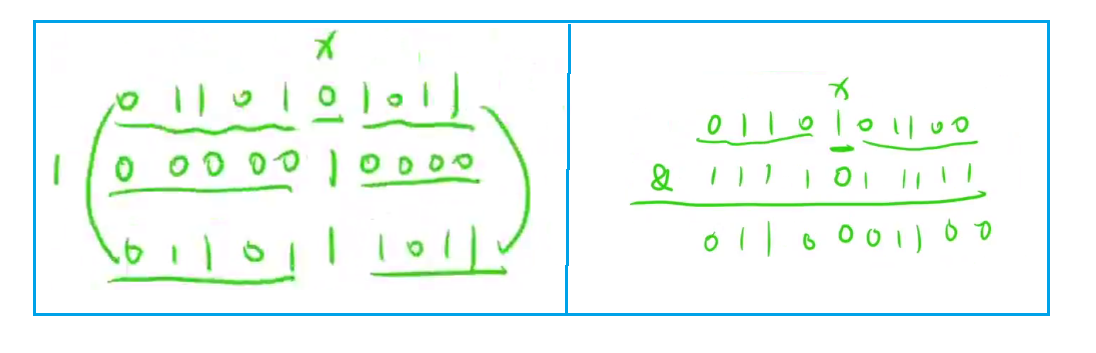
给定一个数 n,确定它的二进制表示中第 x 位是 0 还是 1
(n >> x) & 1
给定一个数 n,把它的二进制表示的第 x 位修改为 1
n |= (1 << x)
给定一个数 n,把它的二进制表示的第 x 位修改为 0
n &= (~ (1 << x))
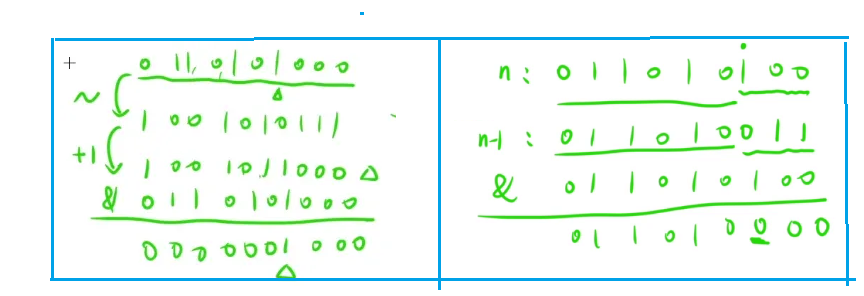
提取一个数 n 二进制表示中最右边的 1
n & -n ( -n 就是将最右侧的 1 左边全部变成相反的,右边不变)
给定一个数 n ,把最右侧的 1 变成 0
n & (n - 1)
亦或(^)运算符运算律
- a ^ a = 0
- a ^ 0 = a
- a ^ b ^ c = a ^ (b ^ c)
3. 例题解析
a. 面试题 01.01. 判定字符是否唯一
如果使用数据结构的话很明显就是放到哈希表中,然后再遍历哈希表进行查找,如果不使用数据结构的话可以通过使用位图的方式来替代哈希表,26 个比特位代表 26 个字母(1 表示该字符已经出现过,0 就表示没有出现过),在遍历字符串的同时进行判断,如果说出现过就直接放回 false ,如果没有就把该位设置为 1
class Solution {
public boolean isUnique(String astr) {
if(astr.length() > 26) return false;
char[] chars = astr.toCharArray();
int bitMap = 0;
for(int i = 0;i < chars.length;i++){
int x = chars[i] - 'a';
if((bitMap >> x & 1) == 1) return false;
else bitMap |= (1 << x);
}
return true;
}
}b. 丢失的数字
方法一:使用哈希表,遍历数组,把数组中的数存在哈希表中并设为 1,再从 0 ~ n 进行遍历,查询哪一位为 0
方法二:高斯求和,把 0 ~ 1 的数进行求和,之后再把数组中的元素都减掉,最后剩的即为所求
方法三:位运算
先把 0 ~ 1的数都进行亦或运算,然后再遍历数组,再进行一次亦或运算,由于 a ^ a = 0,所以重复出现的都被变为 0 了,最后再根据 a ^ 0 = a 知道,剩余的数肯定就是答案了
class Solution {
public int missingNumber(int[] nums) {
int ans = 0;
for(int i = 0;i <= nums.length;i++){
ans ^= i;
}
for(int i = 0;i < nums.length;i++){
ans ^= nums[i];
}
return ans;
}
}c. 两整数之和
由于题中限制了不能使用 + ,- ,所以可以考虑位运算来解决,在开始提到过亦或操作可以看做是无进位相加,所以只需要把进位找到就行,经过分析发现,只有 1 和 1 的情况会出现进位,也就符合了 & 运算,但此时只是表示哪一位发生了进位,所以需要把结果左移再加上无进位相加的结果即可,不过此时还可能会出现进位,所以上述操作需要重复计算,直到没有进位为止
class Solution {
public int getSum(int a, int b) {
while(b != 0){
int ans = a ^ b;
int up = (a & b) << 1;
a = ans;
b = up;
}
return a;
}
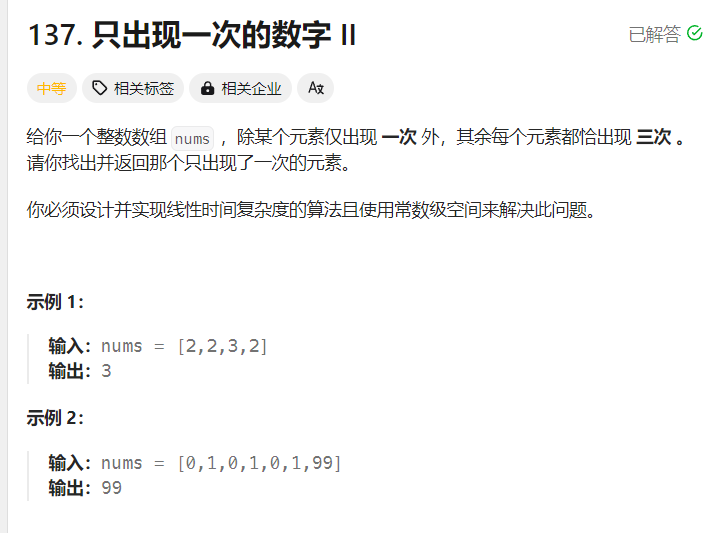
}d. 只出现一次的数字 II
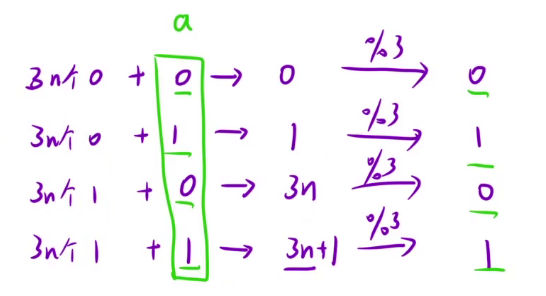
从每一个二进制位相加开始看,所有的数相加最后会有四种情况,把这些情况都 % 3 之后发现,结果和最后剩余那个只出现一次的数的位置相同,所以也就可以从每一个二进制位入手,把所有的数字加起来 % 3,得出每一位的结果,并把目标位设置为结果,最后就是只出现一次的那个数
class Solution {
public int singleNumber(int[] nums) {
int ans = 0;
for(int i = 0;i < 32;i++){
int sum = 0;
for(int x : nums){
if(((x >> i) & 1) == 1){
sum ++;
}
}
if(sum % 3 == 1) ans |= (1 << i);
}
return ans;
}
}e. 面试题 17.19. 消失的两个数字
如果这道题转换一下,先把从 1 到 N 的数亦或,再把结果和 nums 数组亦或,结果也就变成了 nums 数组的数出现了两次,其他的数(也就是缺失的数)出现了一次,就转化为了求消失的两个数字,最终的亦或结果是缺失的那两个数的亦或结果,其中一定可以找到二进制位为 1 的那一位,也就可以把所有的数根据这个位置分为两组,这样也就能够把缺失的这两个数分开,就转化为了找缺失的一位的数,把所有结果亦或,最终就是缺失的那个数字,再求另一组即可
class Solution {
public int[] missingTwo(int[] nums) {
int tmp = 0;
//把 1 ~ n 的数亦或
for(int i = 1;i <= nums.length + 2;i++){
tmp ^= i;
}
//加上数组的数亦或
for(int i = 0;i < nums.length;i++){
tmp ^= nums[i];
}
//找到第一个为 1 的二进制位
int diff = 0;
while(true){
if(((tmp >> diff) & 1) == 1) break;
else diff++;
}
int[] ans = new int[2];
//数组的数分组亦或
for(int i = 0;i < nums.length;i++){
if(((nums[i] >> diff) & 1) == 1) ans[0] ^= nums[i];
else ans[1] ^= nums[i];
}
//1 ~ n 的数分组亦或
for(int i = 1;i <= nums.length + 2;i++){
if(((i >> diff )& 1) == 1) ans[0] ^= i;
else ans[1] ^= i;
}
return ans;
}
}