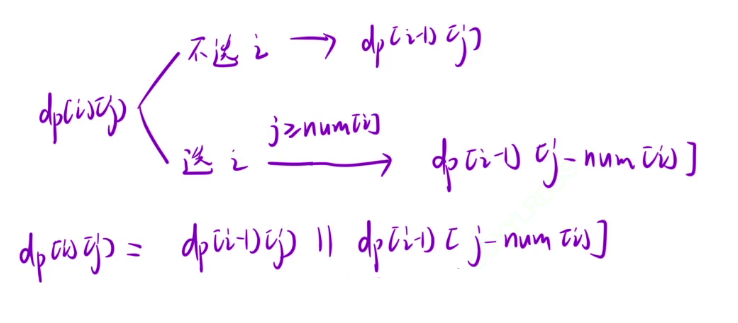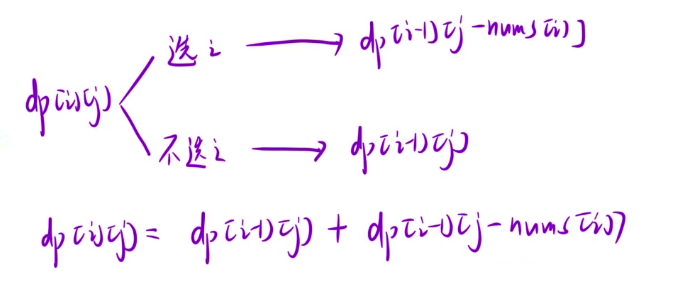1. DP41 【模板】01背包
01 背包就是对于给出的 n 个物品只有选和不选两种选择,每个物品都只能选择一次,题中又分为装满和不一定装满两种情况
1.1. 可以不装满的情况
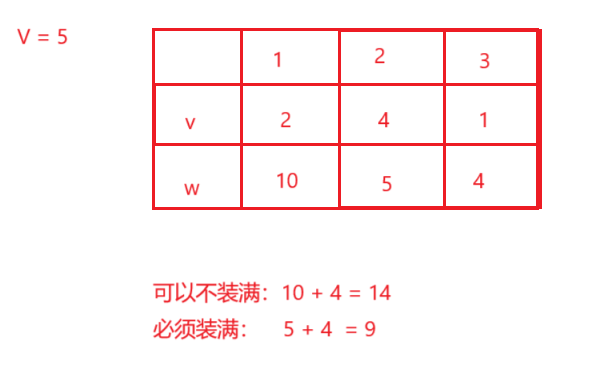
先来看可以不装满的情况:
为了更好的填表,还是从下标为 1 开始填表,dp 数组多开一行和一列
状态表示:
dp[i][j] 表示从前 i 个物品中挑选,总体积不超过 j ,所有选法中,能挑选出来的最大价值
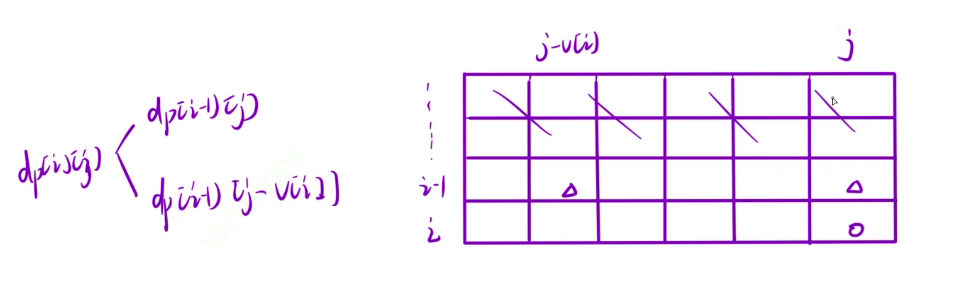
状态转移方程
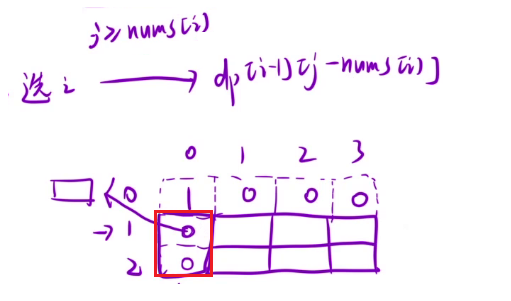
如果不选当前物品的话,那么 dp[i][j] 就等于 dp[i - 1][j],如果选的话,首先需要保证背包剩余容量是可以装下的,然后才能加上当前物品的重量,所以需要判断 j - v[i] 是否是大于 0 的,拿上当前位置的物品之后,背包剩余容量减去当前物品体积,加上当前物品价值,也就是 dp[i - 1][j - v[i]] + w[i]
初始化:i = 0 时,表示有 0 个物品,那么 dp[0][j] 这一行就都是 0,j = 0 时,表示背包容量是 0,也是一件物品都不能装的,所以 dp[i][0] 这一列也都是初始化为 0
填表顺序:从上到下,从左到右
返回值:dp[n][V]
1.2. 需要装满的情况
再来看装满的情况:
状态表示:
dp[i][j] 表示从前 i 个物品中挑选,总体积等于 j ,所有选法中,能挑选出来的最大价值,那么也有可能在前面 i 个物品中挑完之后总体积也是凑不到 j 的,此时就可以用 -1 来表示没有这种情况
状态转移方程:
由于有了凑不出给定的体积的情况,所以状态转移方程也需要稍加调整,当不选 i 物品时,还可以等于前一个物品,但是选的话就需要判断之前可以凑出来需要的体积,也就是 dp[i - 1][j - v[i]] != -1 的情况,然后才可以更新本次结果
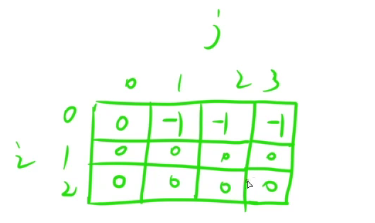
初始化:
当 i = 0 是就是没有物品的情况,dp[0][0] 就是没有物品也没有背包,直接就是 0,但是后面的背包体积 j++ 之后,由于没有物品,也凑不出来体积,所以都初始化为 -1,当 j = 0 时,就是背包体积是 0,此时只要不选物品就可以凑,那么价值也就是 0,所以这一列初始化为 0
填表顺序和返回值都和第一问一样
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int n = in.nextInt(), V = in.nextInt();
int[] v = new int[n + 1];
int[] w = new int[n + 1];
for (int i = 1; i <= n; i++) {
v[i] = in.nextInt();
w[i] = in.nextInt();
}
int[][] dp = new int[n + 1][V + 1];
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= V; j++) {
dp[i][j] = dp[i - 1][j];
if (j >= v[i])
dp[i][j] = Math.max(dp[i][j], dp[i - 1][j - v[i]] + w[i]);
}
}
System.out.println(dp[n][V]);
int[][] dp2 = new int[n + 1][V + 1];
for (int i = 1; i <= V; i++) dp2[0][i] = -1;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= V; j++) {
dp2[i][j] = dp2[i - 1][j];
if (j >= v[i] && dp2[i - 1][j - v[i]] != -1)
dp2[i][j] = Math.max(dp2[i][j], dp2[i - 1][j - v[i]] + w[i]);
}
}
System.out.println(dp2[n][V] == -1 ? 0 : dp2[n][V]);
}
}1.3. 空间优化
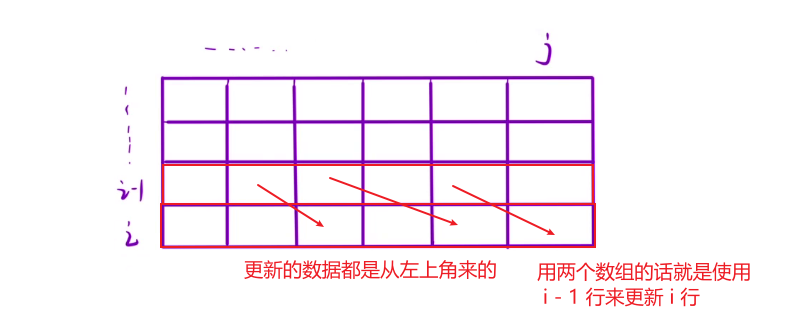
在填 dp[i][j] 位置时,是用上一行来填写当前行的,所以说上面的一大片都是没有用的
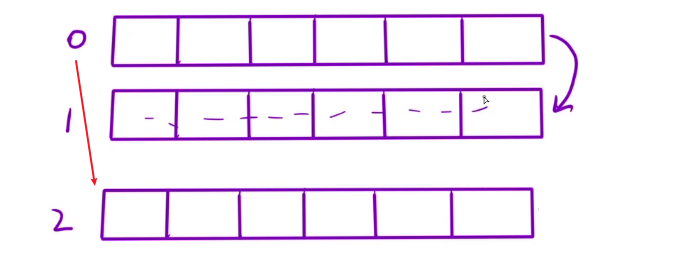
可以利用滚动数组的方式进行优化:
利用第 0 行填完第 1 行之后,直接把第 0 行当做第 2 行,用第一行来填第 2 行,根据这样的方式就把原来 O(n² )的空间复杂度优化为了 O(n) 级别的
还可以继续优化,直接使用一维数组即可:
由于填写当前位置时都是从上一层得来的,并且是从上一层的左边得来的,所以就可以直接通过一维数组每次都从右往左更新,如果还是从左往右更新的话,就会影响右边本来应该更新的值,右边更新是需要左边的,所以左边的值(也就相当于之前的上一层)要等右边更新之后才可以更新
int[] dp = new int[V + 1];
for (int i = 1; i <= n; i++)
for (int j = V; j >= 1; j--)
if (j >= v[i])
dp[j] = Math.max(dp[j], dp[j - v[i]] + w[i]);
System.out.println(dp[V]);
int[] dp2 = new int[V + 1];
for (int i = 1; i <= V; i++) dp2[i] = -1;
for (int i = 1; i <= n; i++)
for (int j = V; j >= 1; j--)
if (j >= v[i] && dp2[j - v[i]] != -1)
dp2[j] = Math.max(dp2[j], dp2[j - v[i]] + w[i]);
System.out.println(dp2[V] == -1 ? 0 : dp2[V]);由于j是递减的,所以当遇到 j < v[i] 时,后面的也就可以不用枚举了,还可以做一个小优化:
for (int j = V; j >= v[i]; j--)
两个问题的循环条件都改为 j >= v[i]
2. 分割等和子集
要把数组分割成两个和相等的子集,其实也就是求在数组中是否能选出一些元素使和等于整个数组和的一半,这就转化为了上面的 01 背包装满的问题,这里的和就相当于背包体积
状态表示:
dp[i][j] 表示在前面 i 个数中选,是否能凑出 j
状态转移方程:
还是分为选和不选两种情况:不选的话就是 dp[i - 1][j],选的话需要 j - num[i] 是大于等于 0 的,这样才可以选,也就是 dp[i - 1][j - num[i]],而 dp[i][j] 的话,只要选和不选其中有任意一种情况可以,那么最终就可以为 true
初始化:第一行 i = 0 表示有 0 个数来使选出和为 j ,所以只有 dp[0][0] 为 true,其它都是 false,而第一列 j = 0 就表示从 i 个数中选出使和为 0 ,只要都不选和就是 0,所以第一列都初始化为 true
填表顺序:从左到右,从上到下
返回值:dp[n][sum/2]
class Solution {
public boolean canPartition(int[] nums) {
int sum = 0;
for(int x : nums) sum+=x;
if(sum % 2 == 1) return false;
int n = nums.length;
int aim = sum / 2;
boolean[][] dp = new boolean[n+1][aim + 1];
for(int i = 1;i <= n;i++) dp[i][0] = true;
dp[0][0] = true;
for(int i = 1;i <= n ;i++){
for(int j = 1;j <= aim;j++){
dp[i][j] = dp[i - 1][j];
if(j >= nums[i - 1]){
dp[i][j] = dp[i - 1][j]||dp[i - 1][j - nums[i - 1]];
}
}
}
return dp[n][aim];
}
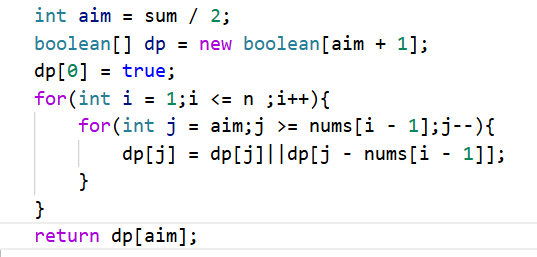
}空间优化和背包问题一样,直接去掉一维数组即可:
3. 目标和
可以先把题目处理一下:
可以把要改成负数的元素加起来得到一个负数的绝对值的和,然后剩余的正数的和减去负数的绝对值的和就是 target,再根据 a + b = sum 可以得出剩下的正数和 a 是等于 (target + sum) / 2 的
然后就变成了从数组中找出一些元素,使它们的和等于 (target + sum) / 2,还是之前的 01 背包模型
状态表示:
dp[i][j] 表示选到第 i 个元素,有多少种和等于 j 的方案
状态转移方程:
当选择第 i 个元素时,还是需要判断是否 j >= nums[i],方案数就是 dp[i - 1][j - nums[i]],不选的话就还是 dp[i - 1][j],最终结果是两种情况的和
初始化:当 i = 0 是还是表示有 0 个元素,所以只有 dp[0][0] 是 1,这一行其它元素都是 0,但是和之前不同的是,这一题数组中的元素是可以为 0 的,所以当 j 等于 0 时,每一行都需要判断是否是 0,这样初始化第 0 列就很麻烦,通过分析可以知道,这一列其实是不用初始化的
这一列越界其实就是选择 i 的这种情况,但是由于用到这个状态是有一个前提条件的,j >= nums[i] ,所以此时的 j 最小就是 0,然后变成了 dp[i - 1][0],还是用到的上一行的状态,并不会用到左上角的状态,所以也不会发生越界,这一列就不用初始化了
填表顺序和返回值和之前一样
class Solution {
public int findTargetSumWays(int[] nums, int target) {
int sum = 0;
for(int x : nums) sum += x;
int n = nums.length;
int aim = (sum + target) / 2;
if((sum + target) % 2 != 0 || aim < 0) return 0;
int[][] dp = new int[n + 1][aim + 1];
dp[0][0] = 1;
for(int i = 1;i <= n;i++){
for(int j = 0;j <= aim;j++){
dp[i][j] = dp[i - 1][j];
if(j >= nums[i - 1]){
dp[i][j] += dp[i - 1][j - nums[i - 1]];
}
}
}
return dp[n][aim];
}
}空间优化:
4. 最后一块石头的重量 II
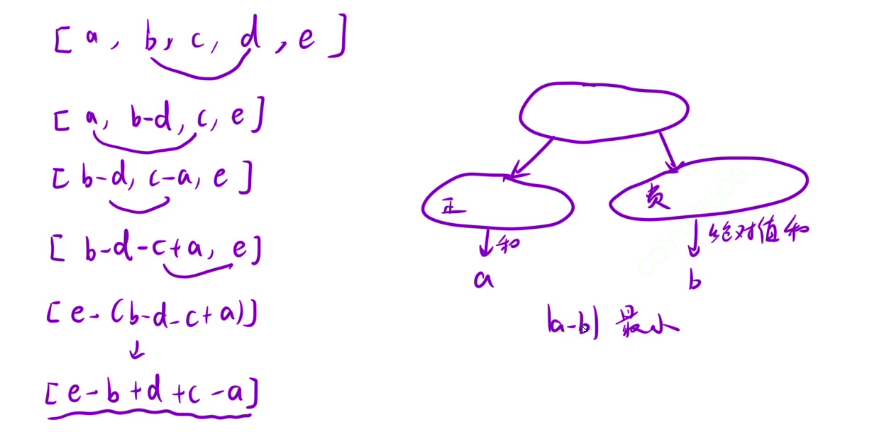
这道题其实还是可以转化为 01 背包的模型的,每两个石头碰撞一下,也就是这两个石头大的减小的的差再继续和其他石头碰,先假设出来一种情况,然后最后的化简结果其实就是给数组中的所有数都加上正号和负号,然后使最终的和最小,这其实和上一题的目标和差不多,这道题也正好符合 01 背包模型,也就是在数组中选出一些数,使这些数的和尽可能接近总和的一半,那么和剩下的相减就能减出最小值了
代码直接套用 01 背包模版就行了,最后的返回值根据题目要求即可