edu111
A. Find The Array
题意
让我们称由
n
n
n正数(大于
0
0
0)组成的数组为
a
a
a如果对于从
1
1
1到
n
n
n的每个
i
i
i都满足以下条件,则整数很漂亮:
a
i
=
1
a_i=1
ai=1
,或者数组中至少存在数字
a
i
−
1
a_i−1
ai−1
和
a
i
−
2
a_i−2
ai−2中的一个。给定
s
s
s,求数组和为
s
s
s的漂亮数组的最小可能大小。
思路
为了满足和为 s s s的同时数组元素最小,那么我们选择每一个元素为其前一个+2是最优的,即构造一个奇数序列,直到其和大于等于 s s s。
代码
#include<bits/stdc++.h>
#define ull unsigned long long
#define ll long long
#define inf 0x3f3f3f3f
#define lc p<<1
#define rc p<<1|1
#define endl '\n'
#define all(a) a.begin()+1,a.end()
#define all0(a) a.begin(),a.end()
#define lowbit(a) (a&-a)
#define fi first
#define se second
#define pb push_back
#define yes cout<<"YES"<<endl
#define no cout<<"NO"<<endl
using namespace std;
const double eps=1e-6;
typedef pair<int,int>PII;
typedef array<int,3>PIII;
mt19937_64 rnd(time(0));
void solve()
{
int s;cin>>s;
for(int i=1;i<=5010;i++)
{
if((1+2*i-1)*i/2>=s) {cout<<i<<endl;return;}
}
}
int main()
{
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
int t;cin>>t;
while(t--)
solve();
return 0;
}
B. Maximum Cost Deletion
题意
您将得到一个长度为 n n n的字符串 s s s其中仅包含字符 0 0 0和 1 1 1。执行以下操作,直到字符串变为空:选择一些相等字符的连续子串,将其从字符串中擦除,并将剩余的两个部分粘合在一起(其中任何一个都可以是空的)按照同样的顺序。例如,如果从字符串 111110 111110 111110中擦除子串 111 111 111,则将得到字符串 110 110 110。删除长度为 l l l的子字符串时,将获得 a ⋅ l + b a⋅l+b a⋅l+b点。您的任务是,如果必须将给定的字符串设置为空,则计算您可以获得的最大总点数.
思路
可以发现只有两种策略
- 1 删的次数尽可能多,即 n n n个字符删 n n n次,那么贡献为 n ∗ ( a + b ) n*(a+b) n∗(a+b)
- 2 删的次数尽可能少,即尽可能地删连续的
0
0
0或
1
1
1,可以证明先删除完
0
0
0或
1
1
1地删除策略是删除次数最少的。计连续子串
0
0
0的个数为
c
n
t
0
cnt0
cnt0,连续子串
1
1
1的个数为
c
n
t
1
cnt1
cnt1,打表发现,如果
c
n
t
0
=
=
c
n
t
1
cnt0==cnt1
cnt0==cnt1,那么最少删除次数为
c
n
t
0
+
1
cnt0+1
cnt0+1,否则最少删除次数为
m
a
x
(
c
n
t
0
,
c
n
t
1
)
max(cnt0,cnt1)
max(cnt0,cnt1),计最少删除次数为
c
n
t
cnt
cnt,那么贡献为
n
∗
a
+
b
∗
c
n
t
n*a+b*cnt
n∗a+b∗cnt。
比较两种策略的贡献取最大值即可。
代码
#include<bits/stdc++.h>
#define ull unsigned long long
#define ll long long
#define inf 0x3f3f3f3f
#define lc p<<1
#define rc p<<1|1
#define endl '\n'
#define all(a) a.begin()+1,a.end()
#define all0(a) a.begin(),a.end()
#define lowbit(a) (a&-a)
#define fi first
#define se second
#define pb push_back
#define yes cout<<"YES"<<endl
#define no cout<<"NO"<<endl
using namespace std;
const double eps=1e-6;
typedef pair<int,int>PII;
typedef array<int,3>PIII;
mt19937_64 rnd(time(0));
void solve()
{
int n,a,b;
cin>>n>>a>>b;
string s;cin>>s;
ll ans1,ans2;
ans1=ans2=0;
int cnt0,cnt1;
cnt0=cnt1=0;
for(int i=0;i<n;i++)
{
if(s[i]=='0')
{
int j=i;
while(j<n && s[j]=='0') j++;
cnt0++;
i=j-1;
}
}
for(int i=0;i<n;i++)
{
if(s[i]=='1')
{
int j=i;
while(j<n && s[j]=='1') j++;
cnt1++;
i=j-1;
}
}
//cout<<cnt0<<" "<<cnt1<<endl;
int cnt=0;
if(cnt0==cnt1) cnt=cnt0+1;
else cnt=max(cnt0,cnt1);
ans1=b*cnt+n*a;
ans2=n*(a+b);
cout<<max(ans1,ans2)<<endl;
}
int main()
{
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
int t;cin>>t;
while(t--)
solve();
return 0;
}
C. Manhattan Subarrays
疑似有点太猜了,(注意力低下导致的
题意
设有三个点
p
,
q
,
r
p,q,r
p,q,r,如果
d
(
p
,
r
)
=
d
(
q
,
p
)
+
d
(
q
,
r
)
d(p,r)=d(q,p)+d(q,r)
d(p,r)=d(q,p)+d(q,r),那么称其为一个坏的三元组,其中
d
(
x
,
y
)
d(x,y)
d(x,y)为x与y的欧几里得距离。
假设数组
b
1
,
b
2
,
…
,
b
m
b_1,b_2,…,b_m
b1,b2,…,bm是好的,如果不可能选择三个不同的索引
i
i
i
,
j
j
j,使得点
(
b
i
,
i
)
(b_i,i)
(bi,i)、
(
b
j
,
j
)
(b_j,j)
(bj,j)和
(
b
k
,
k
)
(b_k,k)
(bk,k)形成坏三元组。您将得到一个数组
a
1
,
a
2
,
…
,
a
n
a_1,a_2,…,a_n
a1,a2,…,an。计算
a
a
a的良好子数组的数量。数
a
a
a的子数组是某些
1
≤
l
≤
r
≤
n
1 \le l \le r \le n
1≤l≤r≤n的数组
a
l
,
a
l
+
1
,
…
,
a
r
a_l,a_{l+1},…,a_r
al,al+1,…,ar。注意,根据定义,长度为
1
1
1和
2
2
2的子数组是好的。
思路
- 1.首先对于三个下标,
i
<
j
<
k
i<j<k
i<j<k,只有满足
a
i
≤
a
j
≤
a
k
a_i \le a_j \le a_k
ai≤aj≤ak 或
a
i
≥
a
j
≥
a
k
a_i \ge a_j \ge a_k
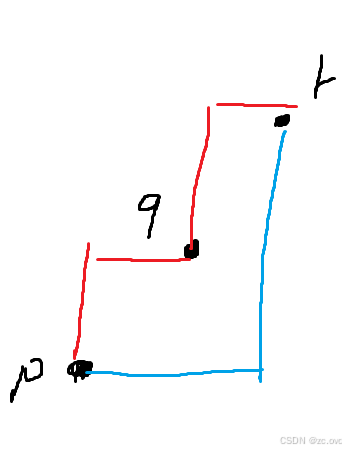
ai≥aj≥ak 才可能是一个坏的三元组,证明如下
其中红色部分之和等于蓝色部分之和
-
2.没看明白的地方,只有长度 ≤ 4 \le 4 ≤4的子数组可能是漂亮的子数组
根据如上策略,长度为 1 和 2 1和2 1和2的子数组贡献为 n + n − 1 n+n-1 n+n−1,再枚举长度为 3 和 4 3和4 3和4的子数组是否满足条件1即可。
代码
#include<bits/stdc++.h>
#define ull unsigned long long
#define ll long long
#define inf 0x3f3f3f3f
#define lc p<<1
#define rc p<<1|1
#define endl '\n'
#define all(a) a.begin()+1,a.end()
#define all0(a) a.begin(),a.end()
#define lowbit(a) (a&-a)
#define fi first
#define se second
#define pb push_back
#define yes cout<<"YES"<<endl
#define no cout<<"NO"<<endl
using namespace std;
const double eps=1e-6;
typedef pair<int,int>PII;
typedef array<int,3>PIII;
mt19937_64 rnd(time(0));
void solve()
{
int n;cin>>n;
vector<int>f(n+1);
for(int i=1;i<=n;i++) cin>>f[i];
ll ans=n+n-1;
auto check=[&](int a,int b,int c)
{
return(f[a]<=f[b] && f[b]<=f[c]) || (f[a]>=f[b] && f[b]>=f[c]);
};
for(int i=1;i<=n-2;i++)
{
if(!check(i,i+1,i+2)) ans++;
}
for(int i=1;i<=n-3;i++)
{
if(!check(i,i+1,i+2) && !check(i,i+1,i+3) && !check(i,i+2,i+3) && !check(i+1,i+2,i+3)) ans++;
}
cout<<ans<<endl;
}
int main()
{
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
int t;cin>>t;
while(t--)
solve();
return 0;
}