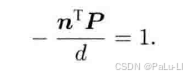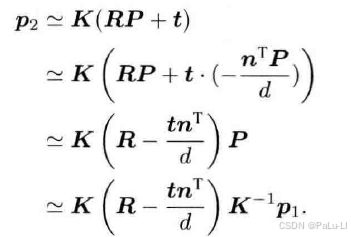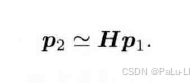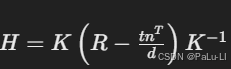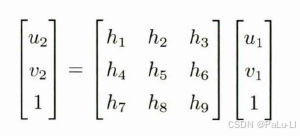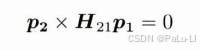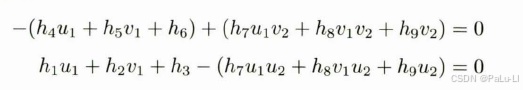前言

单应矩阵主要用于平面场景的位姿估计，例如面对墙或者是地面时。无人机携带的俯视相机，扫地机器人携带的顶视相机这两种情况常见。

1.函数声明 

cv::Mat Initializer::ComputeH21(const vector<cv::Point2f> &vP1,const vector<cv::Point2f> &vP2) 

2.函数定义

1.单应矩阵的推导： 

三维空间上的平面的的点法式方程：

对方程进行变形： 

经过一系列变换： 

得到单应矩阵： 

2.单应矩阵的求解(ComputeH21)： 

1.将变换转换成矩阵关系

2.左右同时×乘p2 

矩阵形式： 

方程形式：

再次转换为矩阵形式： 

只需要4对点即8个约束方程就能求解上述的矩阵方程。 

把H矩阵看成了向量，通过解该向量的线性方程来恢复H,又称直接线性变换法(Direct Linear Transform, DLT)。

对矩阵进行SVD分解，右奇异矩阵的最后一列就是最优解。

3.代码分析 

/*
 用DLT方法求解单应矩阵H
 这里最少用4对点就能够求出来，不过这里为了统一还是使用了8对点求最小二乘解
 vP1               参考帧中归一化后的特征点
 vP2               当前帧中归一化后的特征点
 return cv::Mat              计算的单应矩阵H
 */
cv::Mat Initializer::ComputeH21(
    const vector<cv::Point2f> &vP1, //归一化后的点, in reference frame
    const vector<cv::Point2f> &vP2) //归一化后的点, in current frame
{
 
	//获取参与计算的特征点的数目
    const int N = vP1.size();
 
    // 构造用于计算的矩阵 A 
    cv::Mat A(2*N,				//行，注意每一个点的数据对应两行
			  9,				//列
			  CV_32F);      	//float数据类型
 
	// 构造矩阵A，将每个特征点添加到矩阵A中的元素
    for(int i=0; i<N; i++)
    {
		//获取特征点对的像素坐标
        const float u1 = vP1[i].x;
        const float v1 = vP1[i].y;
        const float u2 = vP2[i].x;
        const float v2 = vP2[i].y;
 
		//生成这个点的第一行
        A.at<float>(2*i,0) = 0.0;
        A.at<float>(2*i,1) = 0.0;
        A.at<float>(2*i,2) = 0.0;
        A.at<float>(2*i,3) = -u1;
        A.at<float>(2*i,4) = -v1;
        A.at<float>(2*i,5) = -1;
        A.at<float>(2*i,6) = v2*u1;
        A.at<float>(2*i,7) = v2*v1;
        A.at<float>(2*i,8) = v2;
 
		//生成这个点的第二行
        A.at<float>(2*i+1,0) = u1;
        A.at<float>(2*i+1,1) = v1;
        A.at<float>(2*i+1,2) = 1;
        A.at<float>(2*i+1,3) = 0.0;
        A.at<float>(2*i+1,4) = 0.0;
        A.at<float>(2*i+1,5) = 0.0;
        A.at<float>(2*i+1,6) = -u2*u1;
        A.at<float>(2*i+1,7) = -u2*v1;
        A.at<float>(2*i+1,8) = -u2;
 
    }
 
    // 定义输出变量，u是左边的正交矩阵U， w为奇异矩阵，vt中的t表示是右正交矩阵V的转置
    cv::Mat u,w,vt;
 
	//使用opencv提供的进行奇异值分解的函数
    cv::SVDecomp(A,							//输入，待进行奇异值分解的矩阵
				 w,							//输出，奇异值矩阵
				 u,							//输出，矩阵U
				 vt,						//输出，矩阵V^T
				 cv::SVD::MODIFY_A | 		//输入，MODIFY_A是指允许计算函数可以修改待分解的矩阵，官方文档上说这样可以加快计算速度、节省内存
				     cv::SVD::FULL_UV);		//FULL_UV=把U和VT补充成单位正交方阵
 
	// 返回最小奇异值所对应的右奇异向量
    // 注意前面说的是右奇异值矩阵的最后一列，但是在这里因为是vt，转置后了，所以是行；由于A有9列数据，故最后一列的下标为8
    return vt.row(8).reshape(0, 			//转换后的通道数，这里设置为0表示是与前面相同
							 3); 			//转换后的行数,对应V的最后一列

}

结束语 

以上就是我学习到的内容，如果对您有帮助请多多支持我，如果哪里有问题欢迎大家在评论区积极讨论，我看到会及时回复。