前言
快速排序是目前综合性能最好的排序,像腾讯,微软等知名IT公司都喜欢考这个。在面试中面试官常常会让你手写一个快速排序。因此今天就带大家来深入了解一下快速排序的多种写法(hoare版本,挖坑法,前后指针法),还有快排的非递归写法(校招常考),快排的时间复杂度分析,快排的缺陷,以及优化方法。
一、快速排序介绍
核心思路
- 确定基准数key
- 调整区间,使调整后的区间满足区间左边的数都小于等于基准数,区间右边的书都大于等于基准数。
- 将基准数左右两边划分为新的区间,重复第一第二步,直至整个区间有序。
二、代码实现
1.hoare版本
我们先来看hoare大佬的版本,这也是最原始的版本。
完整代码
void QuickSort1(int* a, int left, int right)
{
//left == right 区间只有一个数,不需要排序
//left > right 此时L和R交错,区间不存在,同理不需排序
if (left >= right)
return;
int begin = left, end = right;
//左端点取key
int keyi = left;
while (left < right)
{
//如果定义keyi为左端点,那么就要右边先走; 反之,左边先走。
//只有这样才能保证最后L和R相遇的位置的值小于keyi的值。
while (left < right && a[right] >= a[keyi])
right--;
while (left < right && a[left] <= a[keyi])
left++;
Swap(&a[left], &a[right]);
}
Swap(&a[left], &a[keyi]);
keyi = left;
// [begin, keyi-1] keyi [keyi+1, end]
// 递归
QuickSort1(a, begin, keyi - 1);
QuickSort1(a, keyi + 1, end);
}
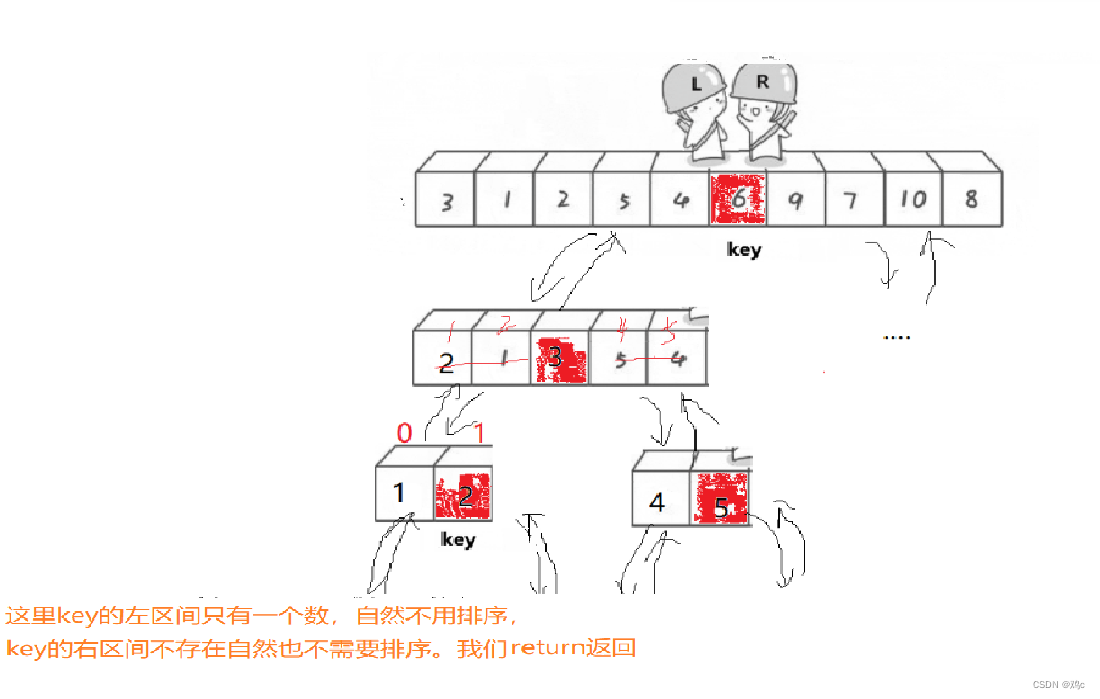
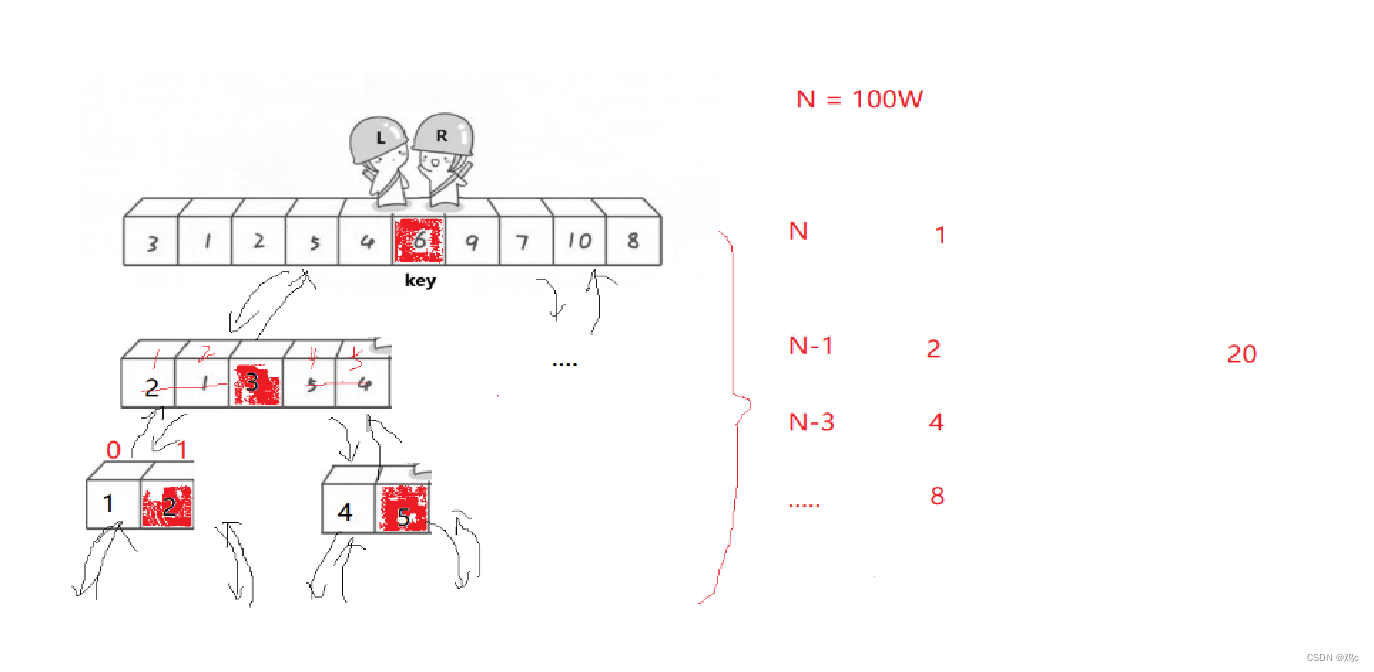
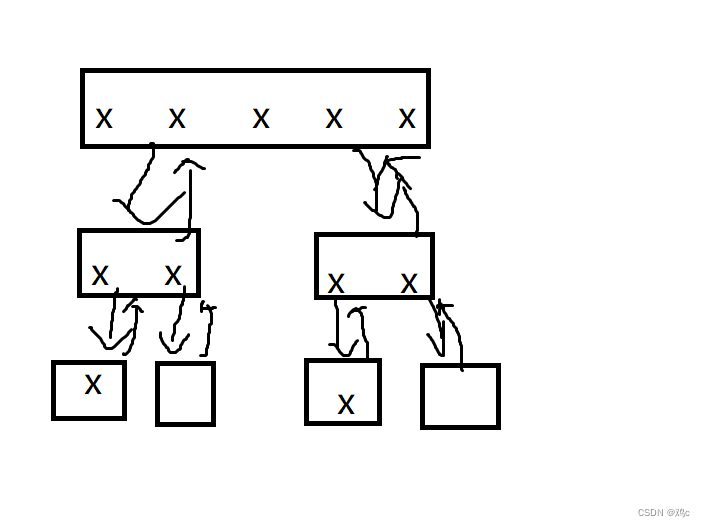
当然这里的过程实际上是在原数组进行的,我这样画只是为了方便大家理解。有没有发现这里和二叉树很像呢?两路递归,先遍历根,在左子树,在右子树,遇到空就返回。
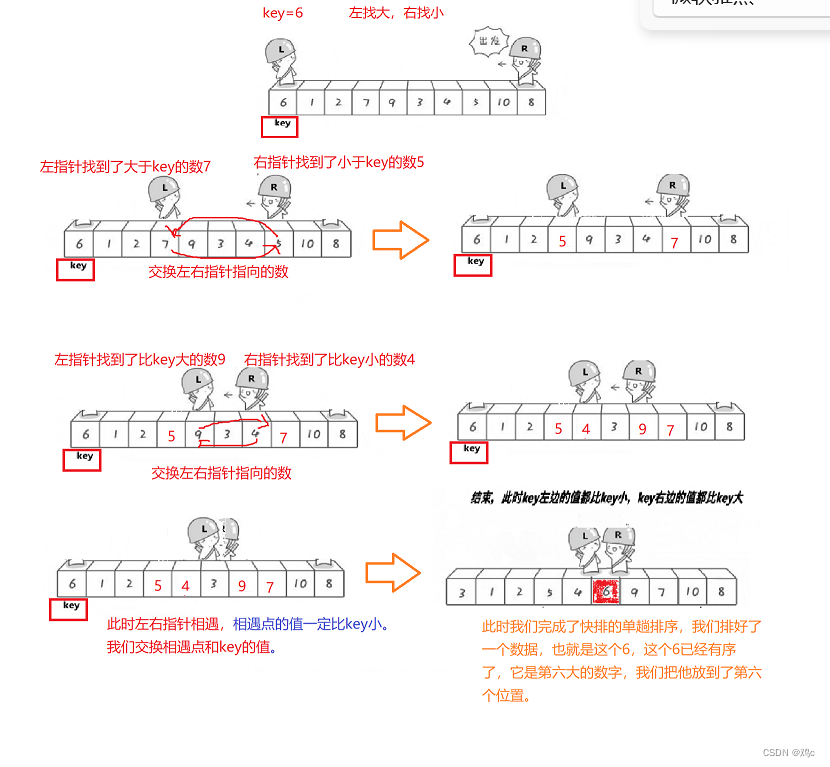
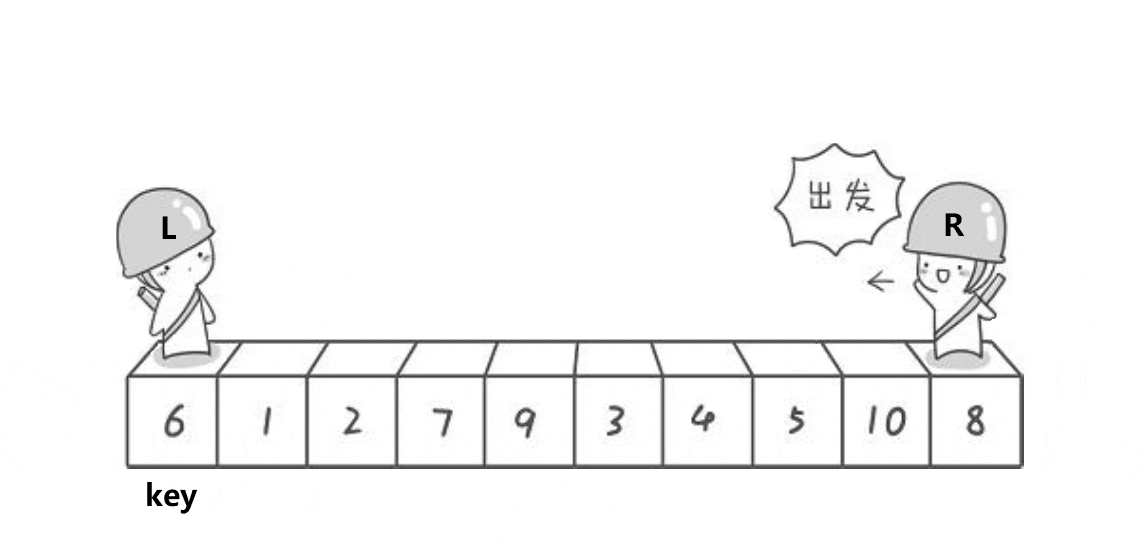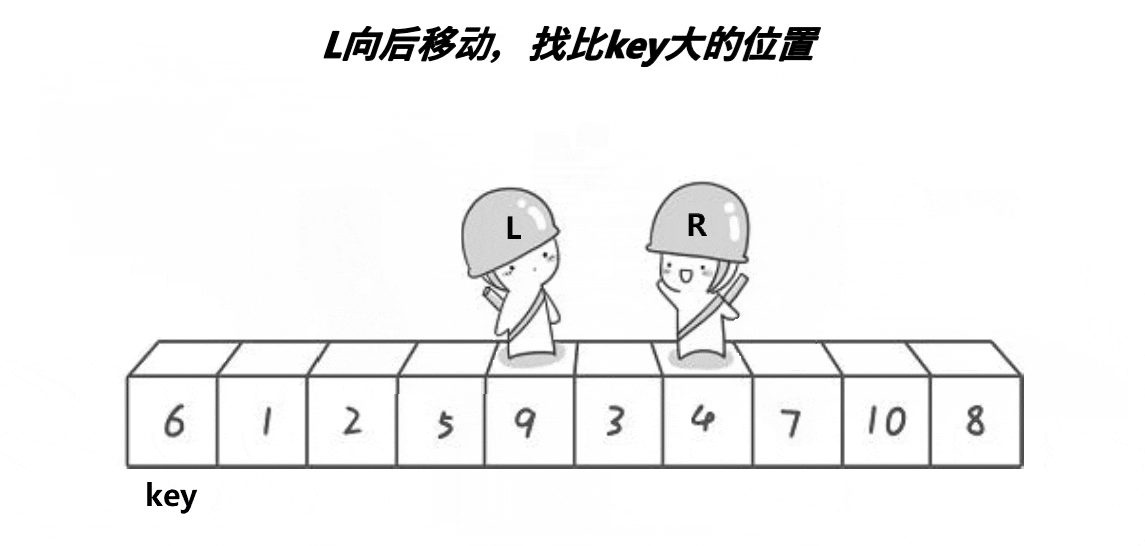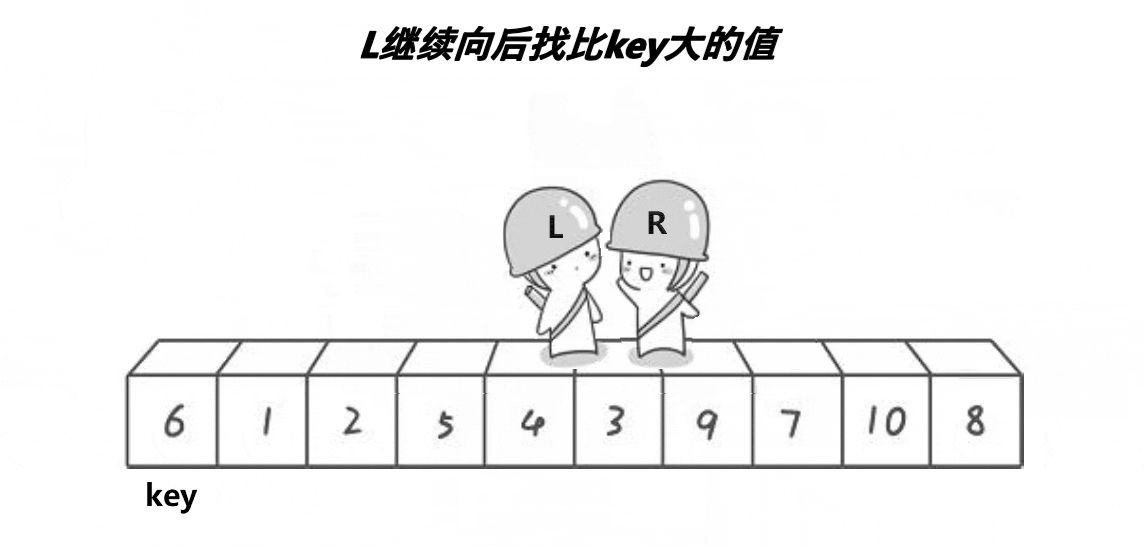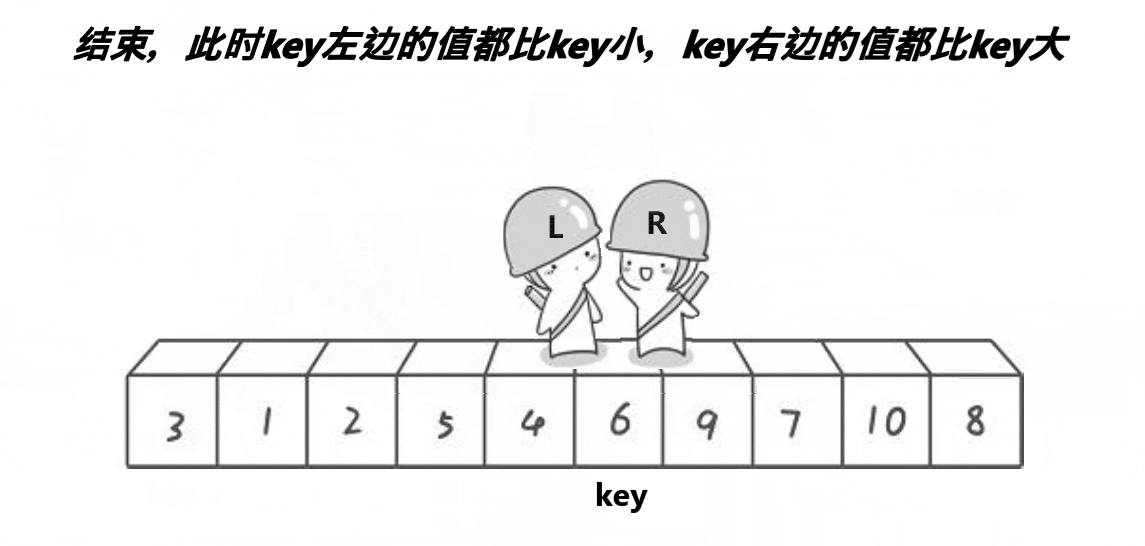
注意:当我们的基准值取左端点时,必须让右指针先走,反之,当基准值取右端点时,必须让左指针先走。这样做的目的是为了保证左指针和右指针相遇的位置的值一定比基准值key小。
下面我们来试试快排的速度。这里我们随机生成了100万个数据,可以看到快排用时75毫秒,堆排用时109毫秒,希尔排序用时110毫秒。
2.挖坑法
完整代码
void QuickSort2(int* a, int left, int right)
{
if (left >= right)
return;
int begin = left, end = right;
//左端点取key
int key = a[left];
int hole = left;
while (left < right)
{
while (left < right && a[right] >= key)
right--;
Swap(&a[right], &a[hole]);
hole = right;
while (left < right && a[left] <= key)
left++;
Swap(&a[left], &a[hole]);
hole = left;
}
a[hole] = key;
// [begin, hole-1] hole [hole+1, end]
// 递归
QuickSort2(a, begin, hole - 1);
QuickSort2(a, hole + 1, end);
}
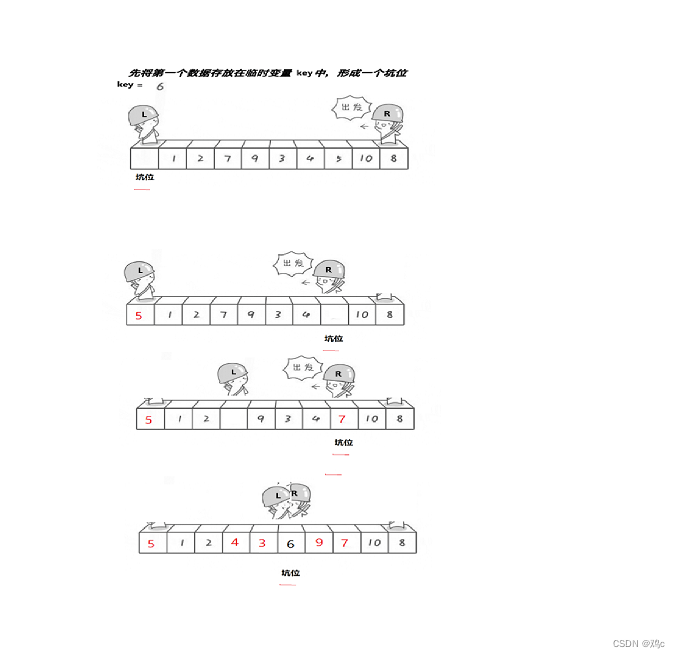
定义一个零时变量key,保存左端点的值,此时左端点形成坑位,右端点移动找小。
找到后把值给坑位,右端点形成新的坑位,左端点移动找大,以此往复。当左右指针相遇,把临时变量key的值给相遇点。
3.前后指针法
- 我们需要定义两个指针cur,prev。
- 初始时,prev指向区间左端点,cur指向prev下一个位置。
- 让cur向右移动,当cur找到了比key小的数,我们就++prev,然后交换cur和prev的位置,然后++cur
- 当cur找到了比key大的值,++cur;
- 当cur走到了区间的最后一个数据的下一个位置,循环结束。
- 我们把prev指向的位置和key交换。
- 此时就完成了快排的单趟排序。
- 接着递归处理左右区间。
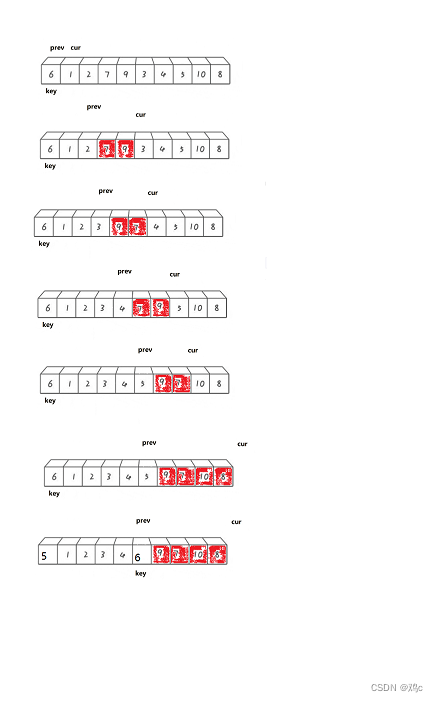
这里的操作可以理解为把比key大的值往右翻,比key小的值,翻到左边。看图理解。
说明:
1.prev要么紧跟着cur(prev下一个就是cur)
2.prev跟cur中间隔着比key大的一段值区间
完整代码
void QuickSort3(int* a, int left, int right)
{
if (left >= right)
return;
int begin = left, end = right;
//左端点取key
int keyi = left;
int prev = left;
int cur = left + 1;
while (cur <= right)
{
if (a[cur] < a[keyi])
{
++prev;
Swap(&a[cur], &a[prev]);
}
cur++;
}
Swap(&a[prev], &a[left]);
keyi = prev;
// [begin, keyi-1] keyi [keyi+1, end]
// 递归
QuickSort3(a, begin, keyi - 1);
QuickSort3(a, keyi + 1, end);
}
三、时间复杂度
1.快排的平均时间复杂度为O(nlogn)。
快排单趟排序需要处理n个数据,而递归的过程又是一颗二叉树(理想情况下),所以它的递归深度为logn,所以总体的时间复杂度为O(nlogn)。
快排的缺陷
快速排序的最坏情况O(n^2)。
当数据有序的情况下,我们的基准值为数据中最大或最小值时,此时单趟排序只能将数据分为一个区间,此时递归深度变为n层,时间复杂度为O(n^2)。
优化方法
1.随机取key
用rand()%(right-left)随机生成一个满足这个区间的下标,然后交换左端点和这个下标的值,我们继续取左端点为基准数。此时基准数为区间内最大或最小值的几率就很低,因为我们排序的数据量很大,多是100W,1000W。注意这里我们需要加上left,
因为这里可能是我们基准数的右区间(我们始终是在数组a上操作的),需要加上left。
void QuickSort3(int* a, int left, int right)
{
if (left >= right)
return;
int begin = left, end = right;
//随机取key
int randi = left + rand() % (right - left);
Swap(&a[left], &a[randi]);
//左端点取key
int keyi = left;
int prev = left;
int cur = left + 1;
while (cur <= right)
{
if (a[cur] < a[keyi])
{
++prev;
Swap(&a[cur], &a[prev]);
}
cur++;
}
Swap(&a[prev], &a[left]);
keyi = prev;
// [begin, keyi-1] keyi [keyi+1, end]
// 递归
QuickSort3(a, begin, keyi - 1);
QuickSort3(a, keyi + 1, end);
}
2.三数取中
三数取中顾名思义就是从三个数中取最终的那个,也就是第二大的数。这里我么一般都是取左端点,右端点和区间中间值三个数。这样取出来的数就一定不会是最大或最小的数了。
这里我们需要用到一个操作两两交换,具体代码在下面。
int GetMidNumi(int*a,int left,int right)
{
int mid = (left + right) / 2;
if (a[left] < a[mid])
{
if (a[mid] < a[right])
{
return mid;
}
//a[mid]>=a[right]
else if (a[left] < a[right])
{
return right;
}
//a[left]>=a[right]
else
{
return left;
}
}
//a[left]>=a[mid]
else
{
if (a[mid] > a[right])
{
return mid;
}
//a[mid]<=a[right]
else if (a[left] < a[right])
{
return left;
}
else
{
return right;
}
}
}
void QuickSort3(int* a, int left, int right)
{
if (left >= right)
return;
int begin = left, end = right;
//三数取中
int midi = GetMidNumi(a, left, right);
if (midi != left)
Swap(&a[left], &a[midi]);
//左端点取key
int keyi = left;
int prev = left;
int cur = left + 1;
while (cur <= right)
{
if (a[cur] < a[keyi])
{
++prev;
Swap(&a[cur], &a[prev]);
}
cur++;
}
Swap(&a[prev], &a[left]);
keyi = prev;
// [begin, keyi-1] keyi [keyi+1, end]
// 递归
QuickSort3(a, begin, keyi - 1);
QuickSort3(a, keyi + 1, end);
}
由于这里两两交换的逻辑稍微有点绕,所以大家在面试中如果需要写快排,可以用随机取key。
3.小区间优化
可以看到当区间只剩下五个数时,我们此时要让它有序,任需要6次递归,由于调用函数需要开辟栈帧,所以消耗较大。我们此时可以对考虑不用递归,使用直接插入排序对区间排序。
//小区间优化
void QucikSort(int* a, int left, int right)
{
if (left >= right)
return;
if (right - left + 1 > 10)
{
int keyi = PartSort1(a, left, right);
QucikSort(a, left, keyi - 1);
QucikSort(a, keyi + 1, right);
}
else
{
InsertSort(a+left, right - left + 1);
}
}
int PartSort1(int* a, int left, int right)
{
int begin = left, end = right;
//三数取中
int midi = GetMidNumi(a, left, right);
if (midi != left)
Swap(&a[left], &a[midi]);
//左端点取key
int keyi = left;
int prev = left;
int cur = left + 1;
while (cur <= right)
{
if (a[cur] < a[keyi])
{
++prev;
Swap(&a[cur], &a[prev]);
}
cur++;
}
Swap(&a[prev], &a[left]);
keyi = prev;
return keyi;
}
四、快排非递归
我们用栈来模拟递归,栈内存入的是区间的左右端点下标。
- 栈里面去一段区间,单趟排序。
- 单趟分割子区间入栈
- 子区间只有一个值或区间不存在就不入栈
- 当栈为空就退出循环
void QuickSortNonR(int* a, int left, int right)
{
ST st;
STInit(&st);
STPush(&st, right);
STPush(&st, left);
while (!STEmpty(&st))
{
int begin = STTop(&st);
STPop(&st);
int end = STTop(&st);
STPop(&st);
int keyi = PartSort1(a, begin, end);
// [begin,keyi-1] keyi [keyi+1, end]
if (keyi + 1 < end)
{
STPush(&st, end);
STPush(&st, keyi + 1);
}
if (begin < keyi - 1)
{
STPush(&st, keyi - 1);
STPush(&st, begin);
}
}
STDestroy(&st);
}