💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
💥1 概述
文献来源:
摘要:本文提出了一种基于神经网络的数据驱动迭代学习控制(ILC)算法,用于解决具有未知模型和重复任务的非线性单输入单输出(SISO)离散时间系统的轨迹跟踪问题。控制目标是使系统的输出在每次迭代过程中跟踪参考轨迹。因此,在每次迭代过程中的每个相对时间点,使用广义回归神经网络(GRNN)作为估计器来解决系统的关键参数,使用径向基函数神经网络(RBFNN)作为控制器来解决控制输入。与传统的ILC算法相比,动态线性化和准则函数最小化这两个复杂的求解过程被替换并简化为GRNN和RBFNN的迭代训练。所提出的算法是开箱即用的,并采用逐点方法计算系统迭代的每个相对时间点的控制输入,使系统的跟踪误差接近于零。此外,证明了在所提出的控制算法下,系统的跟踪误差是一致最终有界的。最后,通过数值示例展示了控制算法的有效性和优越性,无人车的路径跟踪实验进一步验证了其实用性。
关键词:数据驱动 迭代学习控制 GRNN RBFNN 跟踪误差
📚2 运行结果
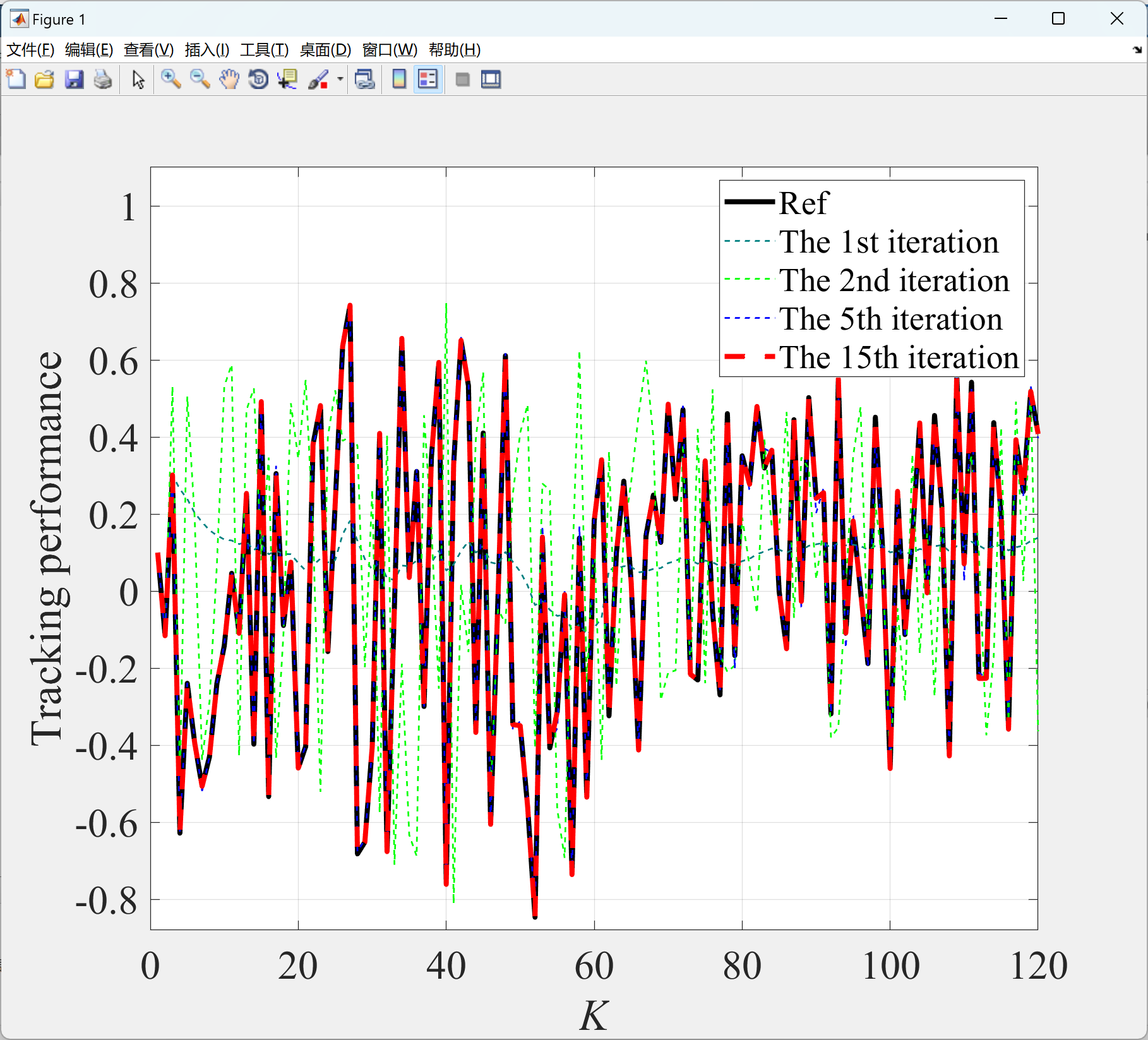
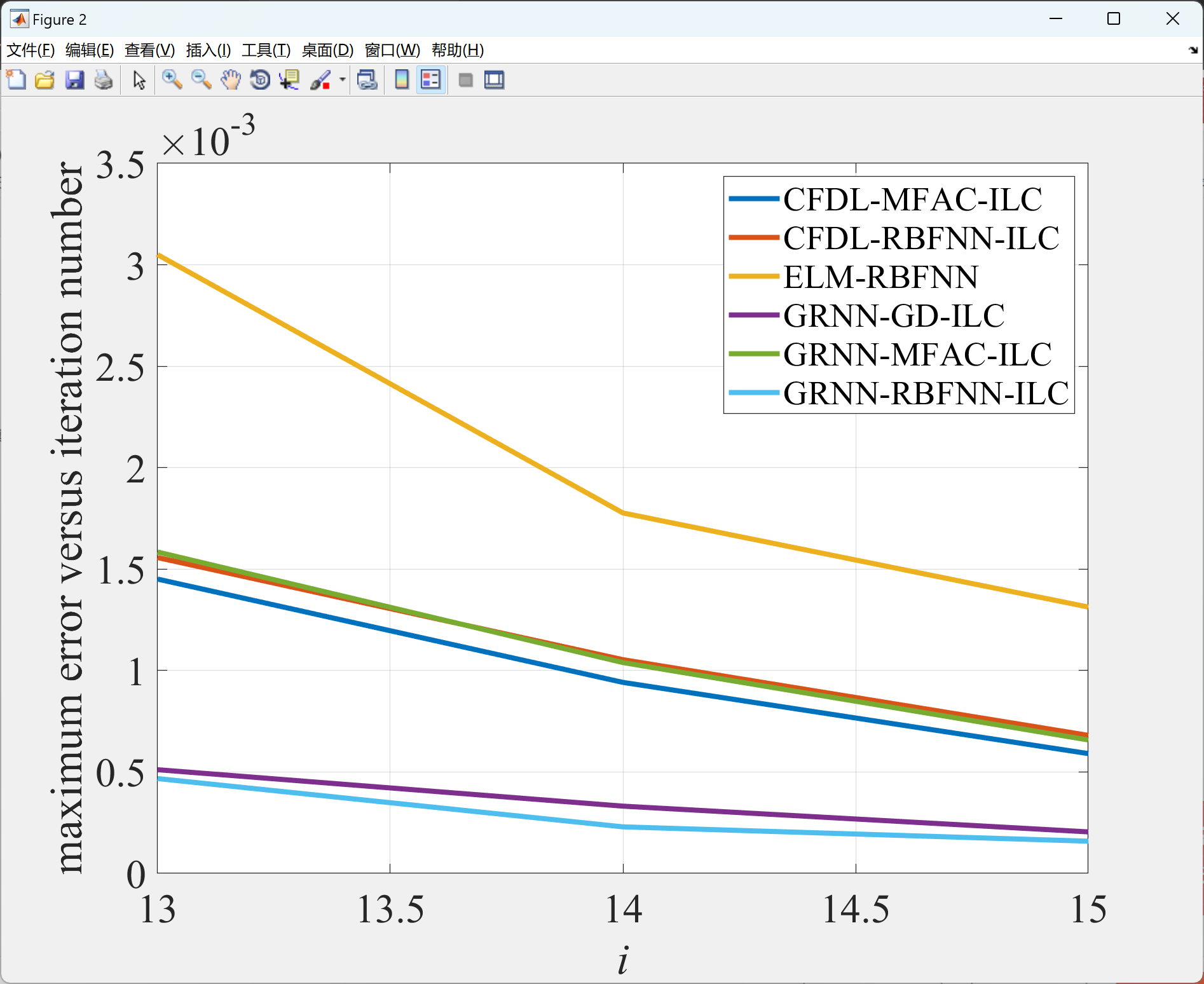
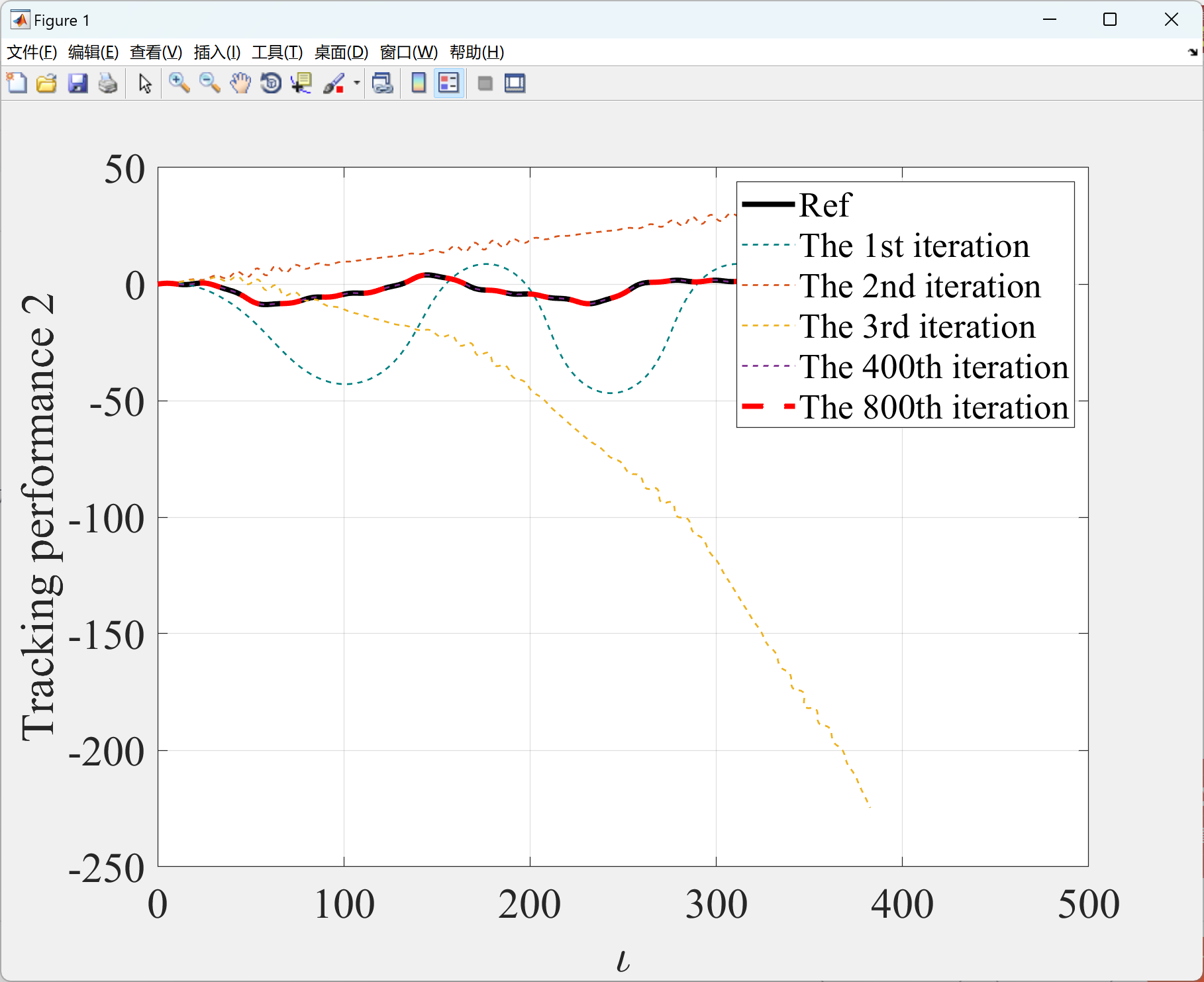
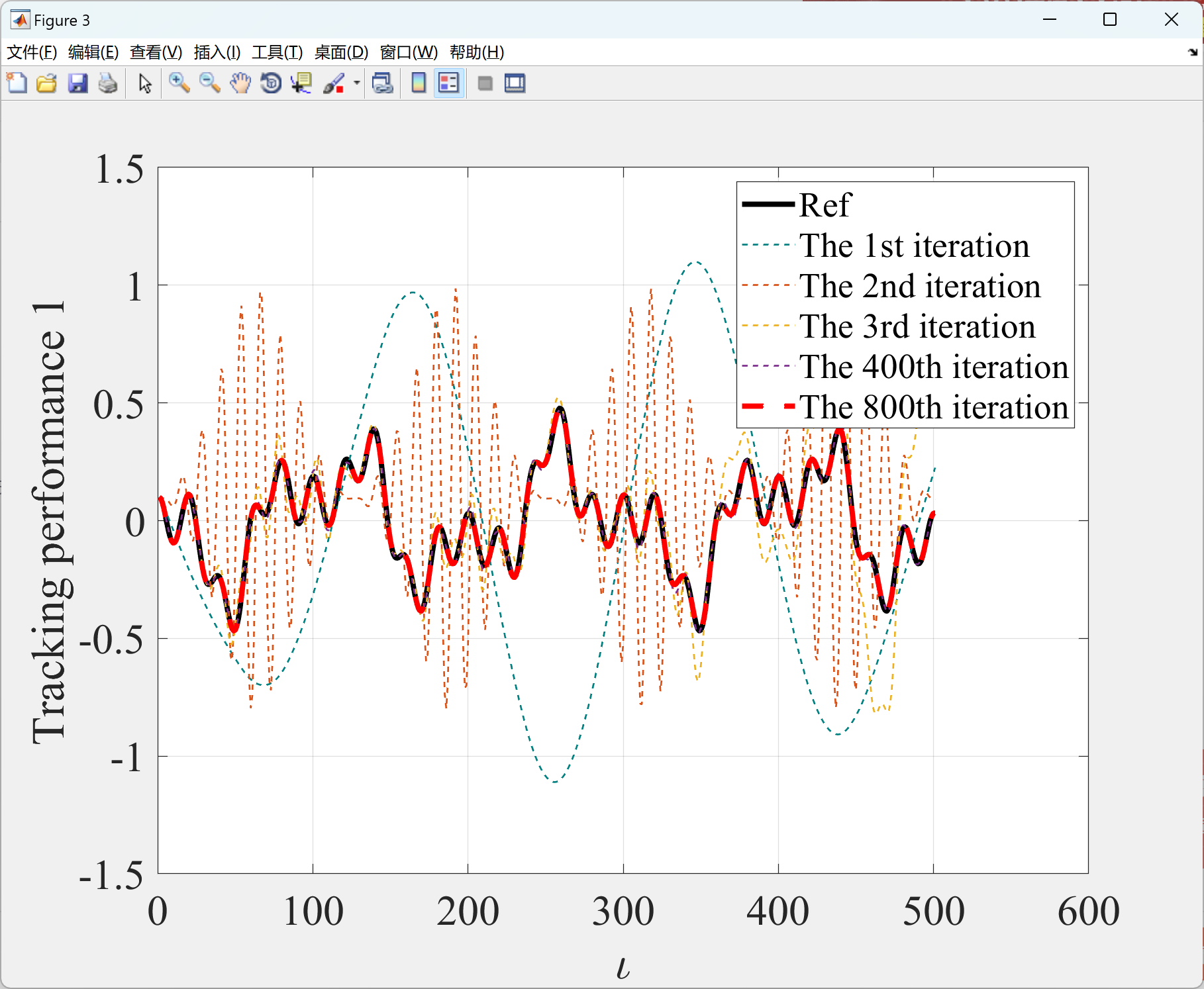
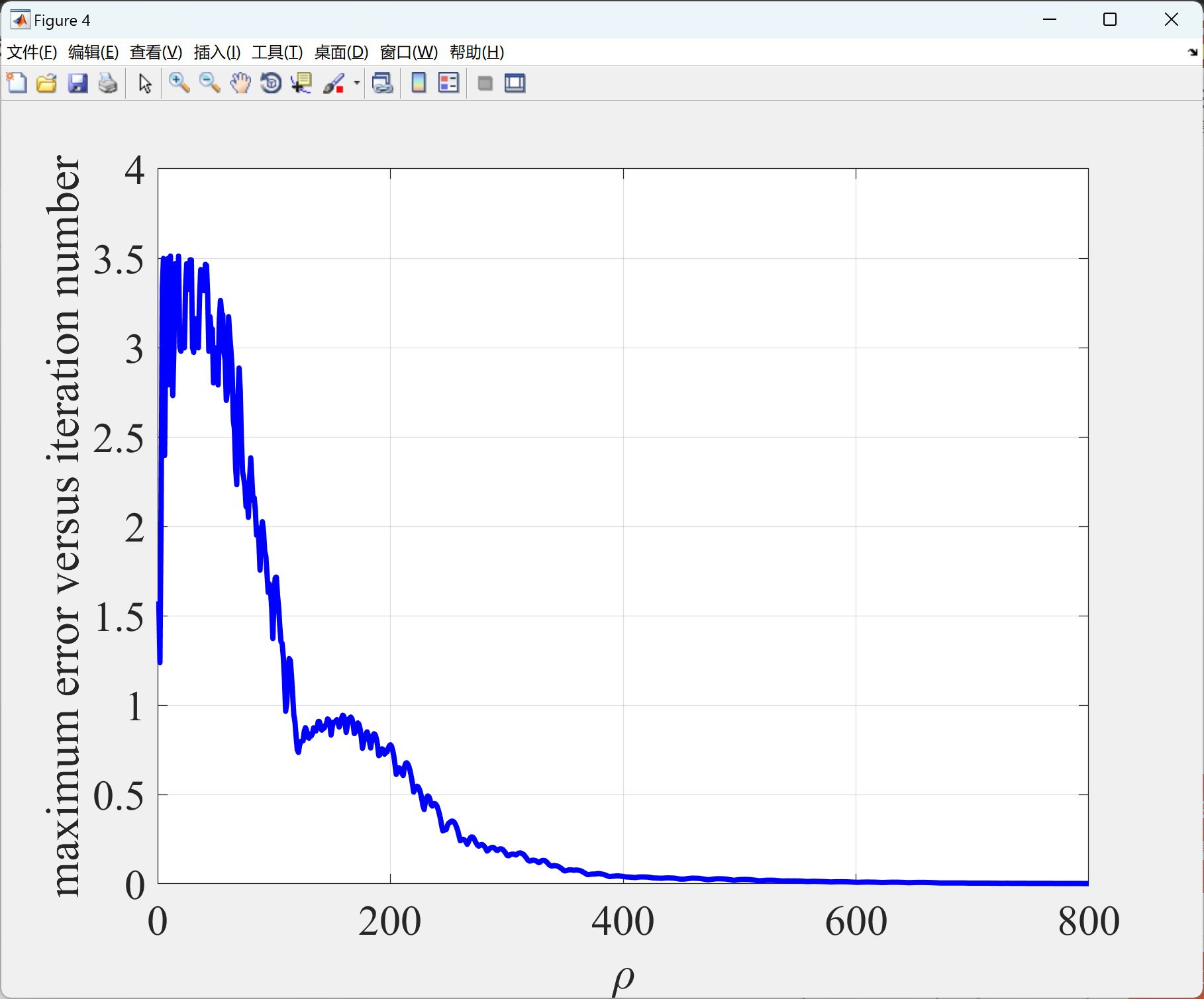
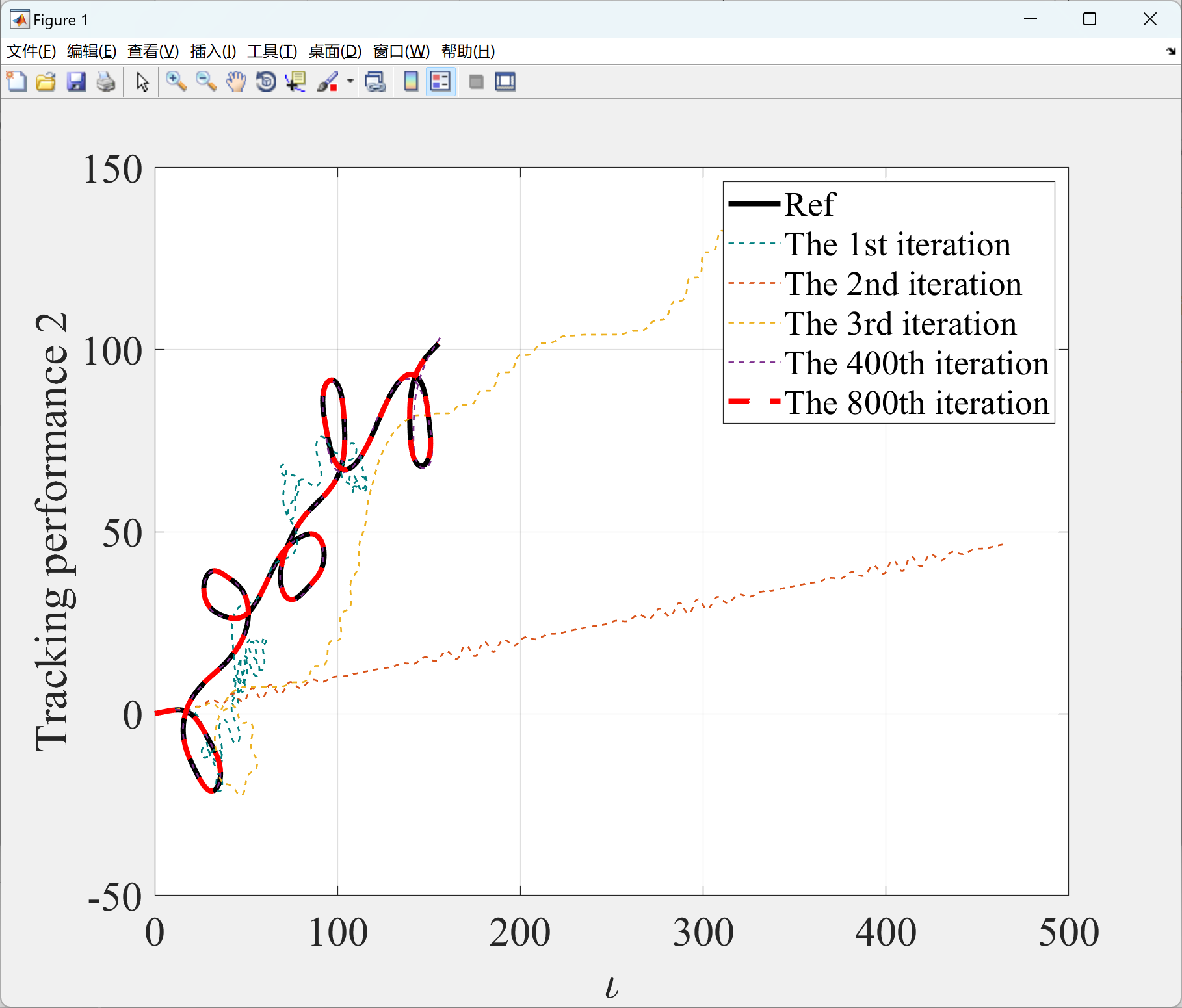
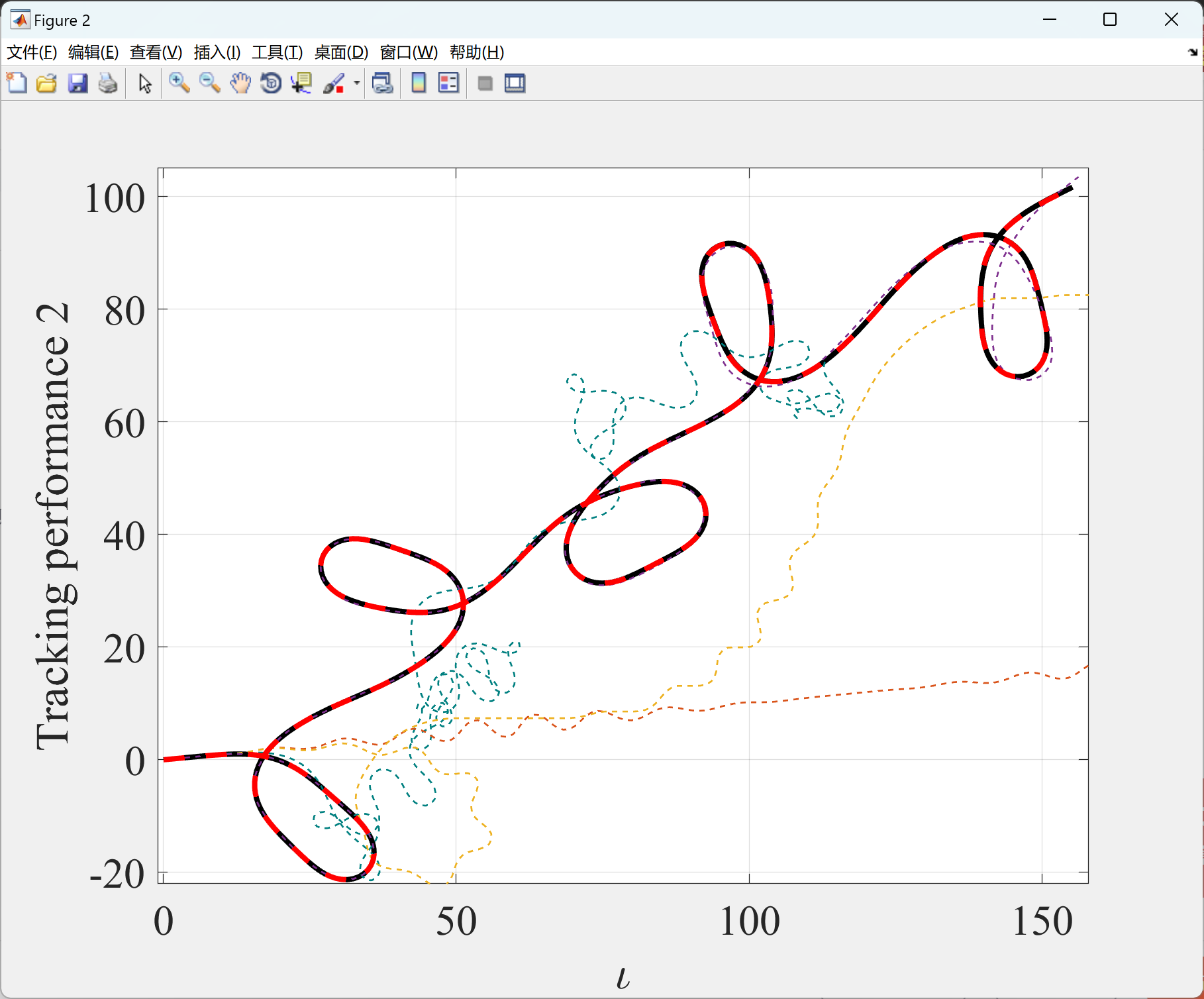
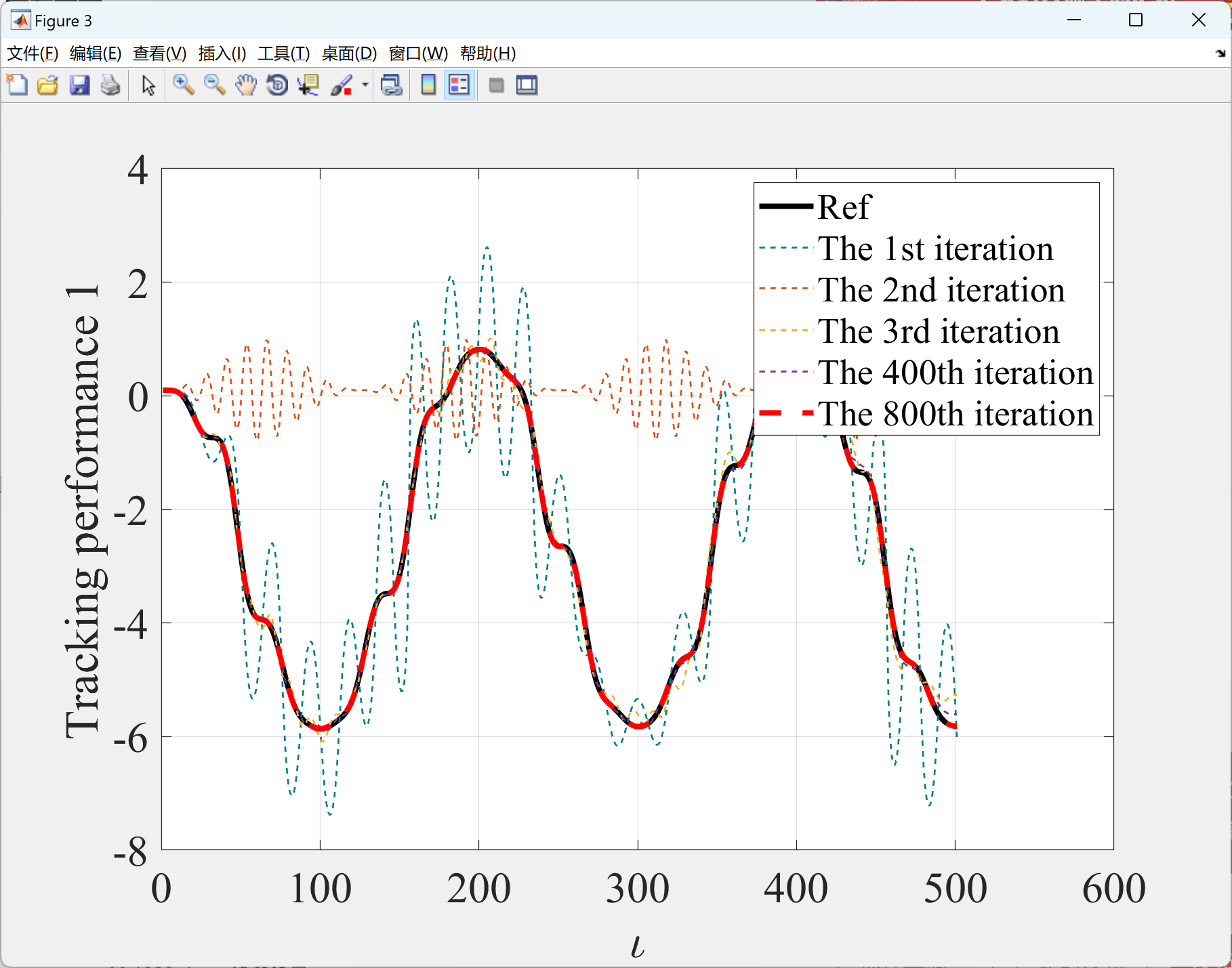
本文展示了使用GRNN-RBFNN-ILC算法实现控制系统的有效性。在第一部分中的程序展示了复杂重复SISO系统的轨迹跟踪控制效果,而在第二部分中的程序展示了系统最大误差的演变。此外,在第3部分中的程序分别展示了使用GRNN-RBFNN-ILC算法实现无人车跟踪参考路径1和参考路径2的效果,而第4部分中的程序展示了这两个示例中车辆最大误差的演变。这些程序可以更好地理解和应用GRNN-RBFNN-ILC算法。
2.1 第1部分
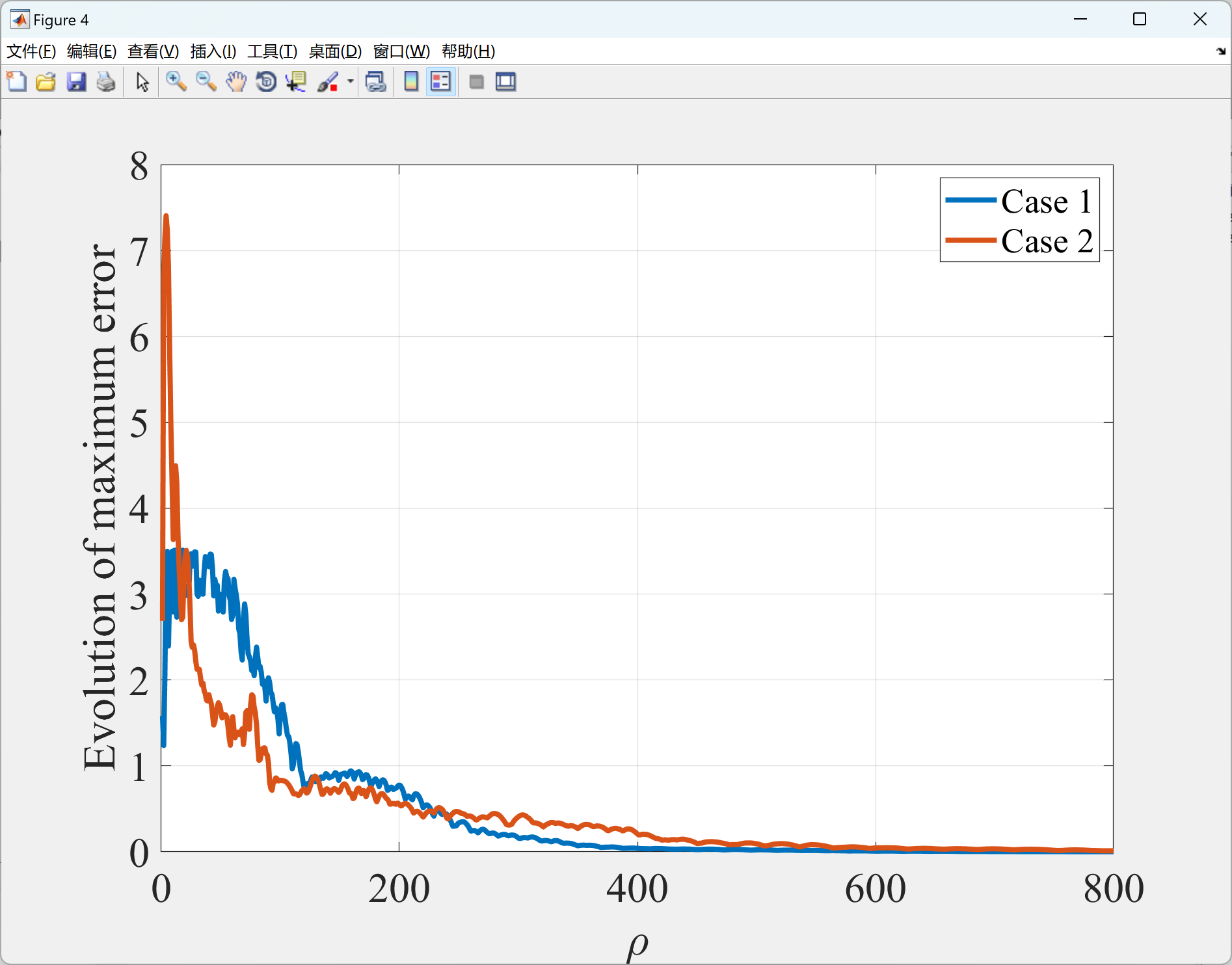
2.2 第2部分
2.3 第3部分
2.4 第4部分
部分代码:
%% 期望轨迹
load pd.mat
% figure
% plot(pd,'r')
% hold on
ypd = pd;
pd = ypd;
%% maxmin约束
q_max = 100;
q_min = -100;
MFAC_ILC_max = 100;
MFAC_ILC_min = 0;
% cm_11 = 0.1;
% rm_11 = 1;
%
% cm_q1 = 0.01;
% rm_q1 = 15;
%
% lammd1 = 2;
cm_11 = 0.01;
rm_11 = 100;
cm_q1 = 0.001;
rm_q1 = 100;
lammd1 = 2;
%% 载入信息
load p1_i1.mat
load q1_i1.mat
load MFAC_ILC11_i1.mat
k_length = length(p1_i1)-1;
%% 第一次迭代
for k = 1:1:k_length
% 输入
q(1, k) = q1_i1(k);
% 输出
p(1, k) = p1_i1(k);
p(1, k + 1) = p1_i1(k + 1);
% 伪雅可比矩阵
MFAC_ILC(1, k) = MFAC_ILC11_i1(k);
fenzi_11(1,k) = 0;
fenmu_11(1,k) = 0;
W_i_k_q1(2,k) = (2 * rand(1) - 1);
e(1,k) = pd(k) - p(1,k);
e(1,k+1) = pd(k+1) - p(1,k+1);
end
%% 第二次迭代
i = 2;
for k = 1:1:k_length
if k == 1
p(i, k) = pd(k);
e(i, k) = pd(k) - p(i, k);
q(i, k) = q1_i1(k);
a = 0.3 + 0.3*round(k / 50);
p(i, k + 1) = 0.4 * sin(q(i, k)) + ( a * q(i, k) ) ;
e(i, k + 1) = pd(k + 1) - p(i, k + 1);
else
MFAC_ILC_isub1_k = MFAC_ILC(i-1, k);
q_isub1_k = q(i-1, k);
q_isub2_k = 0;
p_isub1_kadd1 = p(i-1, k+1);
p_isub2_kadd1 = 0;
%% 11
delta_g11_isub1_kadd1 = [
MFAC_ILC_isub1_k;
q_isub1_k;
q_isub2_k;
p_isub2_kadd1;
p_isub1_kadd1
];
🎉3 参考文献
文章中一些内容引自网络,会注明出处或引用为参考文献,难免有未尽之处,如有不妥,请随时联系删除。
https://xueshu.baidu.com/usercenter/paper/show?paperid=1t2m0p70ys1b0mc05m1n0a50m9468204&site=xueshu_se&hitarticle=1