一、vector的概念
vector是一个功能强大的模板类,用于表示动态数组。
动态大小调整:
std::vector可以根据需要自动增长或收缩其存储的元素数量。这意味着你不需要在创建时就确定确切的大小,可以在运行时根据实际情况添加或删除元素。
连续存储:
std::vector中的元素在内存中是连续存储的。这使得随机访问非常高效,因为可以通过简单的指针算术来计算元素的地址。
连续存储的特性也使得std::vector可以方便地与 C 风格的数组进行交互,并且可以使用迭代器进行高效的遍历。
二、vector的使用
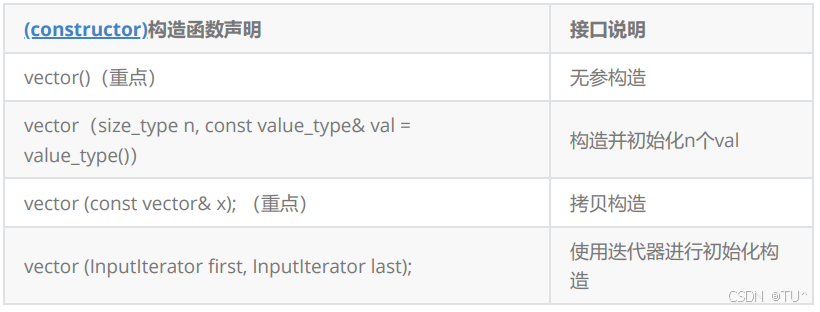
- vector的构造
// vector的构造
void TestVector1()
{
// constructors used in the same order as described above:
vector<int> first; // empty vector of ints
vector<int> second(4, 100); // four ints with value 100
vector<int> third(second.begin(), second.end()); // iterating through second
vector<int> fourth(third); // a copy of third
}
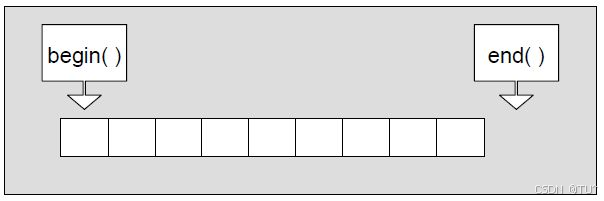
2.vector iterator 的使用
// vector的迭代器
void PrintVector(const vector<int>& v)
{
// const对象使用const迭代器进行遍历打印
vector<int>::const_iterator it = v.begin();
while (it != v.end())
{
cout << *it << " ";
++it;
}
cout << endl;
}
void TestVector2()
{
// 使用push_back插入4个数据
vector<int> v;
v.push_back(1);
v.push_back(2);
v.push_back(3);
v.push_back(4);
// 使用迭代器进行遍历打印
vector<int>::iterator it = v.begin();
while (it != v.end())
{
cout << *it << " ";
++it;
}
cout << endl;
// 使用迭代器进行修改
it = v.begin();
while (it != v.end())
{
*it *= 2;
++it;
}
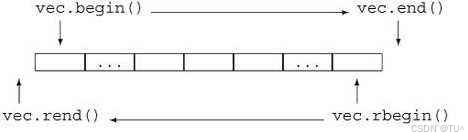
// 使用反向迭代器进行遍历再打印
// vector<int>::reverse_iterator rit = v.rbegin();
auto rit = v.rbegin();
while (rit != v.rend())
{
cout << *rit << " ";
++rit;
}
cout << endl;
PrintVector(v);
}
3.vector 空间增长问题
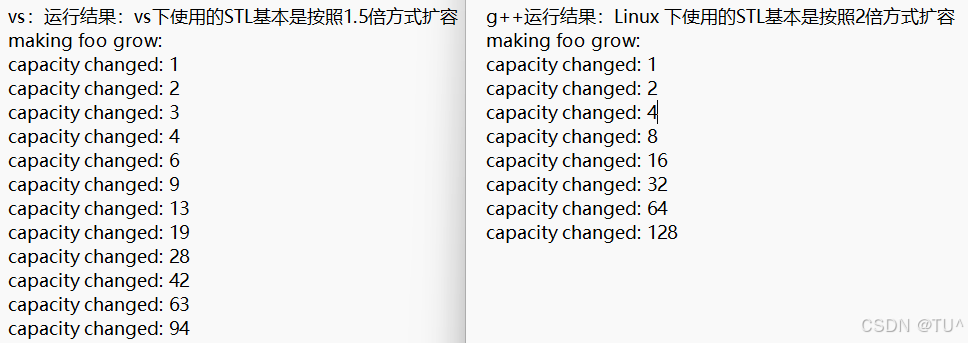
- capacity的代码在vs和g++下分别运行会发现,vs下capacity是按1.5倍增长的,g++是按2
倍增长的。这个问题经常会考察,不要固化的认为,vector增容都是2倍,具体增长多少是
根据具体的需求定义的。vs是PJ版本STL,g++是SGI版本STL。 - reserve只负责开辟空间,如果确定知道需要用多少空间,reserve可以缓解vector增容的代
价缺陷问题。 - resize在开空间的同时还会进行初始化,影响size。
// 测试vector的默认扩容机制
void TestVectorExpand()
{
size_t sz;
vector<int> v;
sz = v.capacity();
cout << "making v grow:\n";
for (int i = 0; i < 100; ++i)
{
v.push_back(i);
if (sz != v.capacity())
{
sz = v.capacity();
cout << "capacity changed: " << sz << '\n';
}
}
}
// 如果已经确定vector中要存储元素大概个数,可以提前将空间设置足够
// 就可以避免边插入边扩容导致效率低下的问题了
void TestVectorExpandOP()
{
vector<int> v;
size_t sz = v.capacity();
v.reserve(100); // 提前将容量设置好,可以避免一遍插入一遍扩容
cout << "making bar grow:\n";
for (int i = 0; i < 100; ++i)
{
v.push_back(i);
if (sz != v.capacity())
{
sz = v.capacity();
cout << "capacity changed: " << sz << '\n';
}
}
}
vector的 resize 和 reserve
// vector的resize 和 reserve
// reisze(size_t n, const T& data = T())
// 将有效元素个数设置为n个,如果时增多时,增多的元素使用data进行填充
// 注意:resize在增多元素个数时可能会扩容
void TestVector3()
{
vector<int> v;
// set some initial content:
for (int i = 1; i < 10; i++)
v.push_back(i);
v.resize(5);
v.resize(8, 100);
v.resize(12);
cout << "v contains:";
for (size_t i = 0; i < v.size(); i++)
cout << ' ' << v[i];
cout << '\n';
}
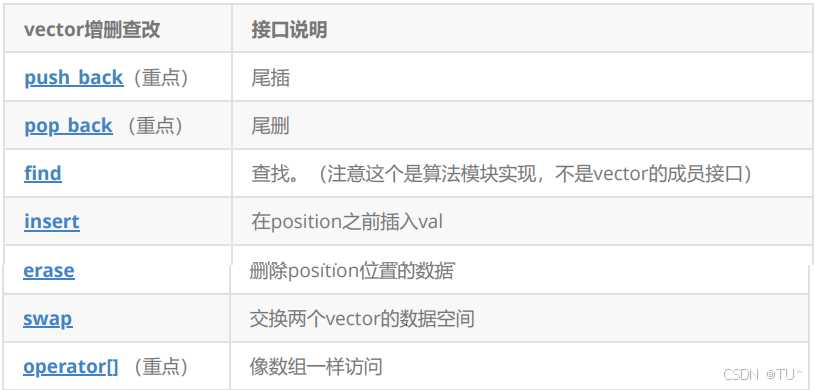
4.vector 增删查改
push_back/pop_back
// vector的增删改查
// 尾插和尾删:push_back/pop_back
void TestVector4()
{
vector<int> v;
v.push_back(1);
v.push_back(2);
v.push_back(3);
v.push_back(4);
auto it = v.begin();
while (it != v.end())
{
cout << *it << " ";
++it;
}
cout << endl;
v.pop_back();
v.pop_back();
it = v.begin();
while (it != v.end())
{
cout << *it << " ";
++it;
}
cout << endl;
}
insert和erase,以及查找find
// 任意位置插入:insert和erase,以及查找find
// 注意find不是vector自身提供的方法,是STL提供的算法
void TestVector5()
{
// 使用列表方式初始化,C++11新语法
vector<int> v{ 1, 2, 3, 4 };
// 在指定位置前插入值为val的元素,比如:3之前插入30,如果没有则不插入
// 1. 先使用find查找3所在位置
// 注意:vector没有提供find方法,如果要查找只能使用STL提供的全局find
auto pos = find(v.begin(), v.end(), 3);
if (pos != v.end())
{
// 2. 在pos位置之前插入30
v.insert(pos, 30);
}
vector<int>::iterator it = v.begin();
while (it != v.end())
{
cout << *it << " ";
++it;
}
cout << endl;
pos = find(v.begin(), v.end(), 3);
// 删除pos位置的数据
v.erase(pos);
it = v.begin();
while (it != v.end()) {
cout << *it << " ";
++it;
}
cout << endl;
}
operator[]+index
// operator[]+index 和 C++11中vector的新式for+auto的遍历
// vector使用这两种遍历方式是比较便捷的。
void TestVector6()
{
vector<int> v{ 1, 2, 3, 4 };
// 通过[]读写第0个位置。
v[0] = 10;
cout << v[0] << endl;
// 1. 使用for+[]小标方式遍历
for (size_t i = 0; i < v.size(); ++i)
cout << v[i] << " ";
cout << endl;
vector<int> swapv;
swapv.swap(v);
cout << "v data:";
for (size_t i = 0; i < v.size(); ++i)
cout << v[i] << " ";
cout << endl;
// 2. 使用迭代器遍历
cout << "swapv data:";
auto it = swapv.begin();
while (it != swapv.end())
{
cout << *it << " ";
++it;
}
// 3. 使用范围for遍历
for (auto x : v)
cout << x << " ";
cout << endl;
}
三、vector 迭代器失效问题
迭代器的主要作用就是让算法能够不用关心底层数据结构,其底层实际就是一个指针,或者是对
指针进行了封装,比如:vector的迭代器就是原生态指针T* 。因此迭代器失效,实际就是迭代器
底层对应指针所指向的空间被销毁了,而使用一块已经被释放的空间,造成的后果是程序崩溃(即
如果继续使用已经失效的迭代器,程序可能会崩溃)。
对于vector可能会导致其迭代器失效的操作有:
- 会引起其底层空间改变的操作,都有可能是迭代器失效,比如:resize、reserve、insert、
assign、push_back等。
#include <iostream>
using namespace std;
#include <vector>
int main()
{
vector<int> v{1,2,3,4,5,6};
auto it = v.begin();
// 将有效元素个数增加到100个,多出的位置使用8填充,操作期间底层会扩容
// v.resize(100, 8);
// reserve的作用就是改变扩容大小但不改变有效元素个数,操作期间可能会引起底层容量改变
// v.reserve(100);
// 插入元素期间,可能会引起扩容,而导致原空间被释放
// v.insert(v.begin(), 0);
// v.push_back(8);
// 给vector重新赋值,可能会引起底层容量改变
v.assign(100, 8);
/*
出错原因:以上操作,都有可能会导致vector扩容,也就是说vector底层原理旧空间被释
放掉,而在打印时,it还使用的是释放之间的旧空间,在对it迭代器操作时,实际操作的是一块
已经被释放的空间,而引起代码运行时崩溃。
解决方式:在以上操作完成之后,如果想要继续通过迭代器操作vector中的元素,只需给
it重新赋值即可。
*/
while(it != v.end())
{
cout<< *it << " " ;
++it;
}
cout<<endl;
return 0;
}
- 指定位置元素的删除操作–erase
#include<iosteram>
using namespace std;
#include <vector>
int main()
{
int a[] = { 1, 2, 3, 4 };
vector<int> v(a, a + sizeof(a) / sizeof(int));
// 使用find查找3所在位置的iterator
vector<int>::iterator pos = find(v.begin(), v.end(), 3);
// 删除pos位置的数据,导致pos迭代器失效。
v.erase(pos);
cout << *pos << endl; // 此处会导致非法访问
return 0;
}
erase删除pos位置元素后,pos位置之后的元素会往前搬移,没有导致底层空间的改变,理论上讲迭代器不应该会失效,但是:如果pos刚好是最后一个元素,删完之后pos刚好是end的位置,而end位置是没有元素的,那么pos就失效了。因此删除vector中任意位置上元素时,vs就认为该位置迭代器失效了。
- 注意:Linux下,g++编译器对迭代器失效的检测并不是非常严格,处理也没有vs下极端。
// 1. 扩容之后,迭代器已经失效了,程序虽然可以运行,但是运行结果已经不对了
int main()
{
vector<int> v{1,2,3,4,5};
for(size_t i = 0; i < v.size(); ++i)
cout << v[i] << " ";
cout << endl;
auto it = v.begin();
cout << "扩容之前,vector的容量为: " << v.capacity() << endl;
// 通过reserve将底层空间设置为100,目的是为了让vector的迭代器失效
v.reserve(100);
cout << "扩容之后,vector的容量为: " << v.capacity() << endl;
// 经过上述reserve之后,it迭代器肯定会失效,在vs下程序就直接崩溃了,但是linux下不会
// 虽然可能运行,但是输出的结果是不对的
while(it != v.end())
{
cout << *it << " ";
++it;
}
cout << endl;
return 0;
}
程序输出:
1 2 3 4 5
扩容之前,vector的容量为: 5
扩容之后,vector的容量为: 100
0 2 3 4 5 409 1 2 3 4 5
//-------------------------------------------------------------------------------------------------
// 2. erase删除任意位置代码后,linux下迭代器并没有失效
// 因为空间还是原来的空间,后序元素往前搬移了,it的位置还是有效的
#include <vector>
#include <algorithm>
int main()
{
vector<int> v{1,2,3,4,5};
vector<int>::iterator it = find(v.begin(), v.end(), 3);
v.erase(it);
cout << *it << endl;
while(it != v.end())
{
cout << *it << " ";
++it;
}
cout << endl;
return 0;
}
程序可以正常运行,并打印:
4
4 5
//-------------------------------------------------------------------------------------------------
// 3: erase删除的迭代器如果是最后一个元素,删除之后it已经超过end
// 此时迭代器是无效的,++it导致程序崩溃
int main()
{
vector<int> v{1,2,3,4,5};
// vector<int> v{1,2,3,4,5,6};
auto it = v.begin();
while(it != v.end())
{
if(*it % 2 == 0)
v.erase(it);
++it;
}
for(auto e : v)
cout << e << " ";
cout << endl;
return 0;
}
========================================================
// 使用第一组数据时,程序可以运行
[sly@VM-0-3-centos 20220114]$ g++ testVector.cpp -std=c++11
[sly@VM-0-3-centos 20220114]$ ./a.out
1 3 5
=========================================================
// 使用第二组数据时,程序最终会崩溃
[sly@VM-0-3-centos 20220114]$ vim testVector.cpp
[sly@VM-0-3-centos 20220114]$ g++ testVector.cpp -std=c++11
[sly@VM-0-3-centos 20220114]$ ./a.out
Segmentation fault
从上述三个例子中可以看到:SGI STL中,迭代器失效后,代码并不一定会崩溃,但是运行
结果肯定不对,如果it不在begin和end范围内,肯定会崩溃的。
4.与vector类似,string在插入+扩容操作+erase之后,迭代器也会失效
#include <string>
void TestString()
{
string s("hello");
auto it = s.begin();
// 放开之后代码会崩溃,因为resize到20会string会进行扩容
// 扩容之后,it指向之前旧空间已经被释放了,该迭代器就失效了
// 后序打印时,再访问it指向的空间程序就会崩溃
//s.resize(20, '!');
while (it != s.end())
{
cout << *it;
++it;
}
cout << endl;
it = s.begin();
while (it != s.end())
{
it = s.erase(it);
// 按照下面方式写,运行时程序会崩溃,因为erase(it)之后
// it位置的迭代器就失效了
// s.erase(it);
++it;
}
}
迭代器失效解决办法:在使用前,对迭代器重新赋值即可。
四、vector的练习
1.杨辉三角
给定一个非负整数 numRows,生成「杨辉三角」的前 numRows 行。
在「杨辉三角」中,每个数是它左上方和右上方的数的和。
思路:
- 可以使用一个二维向量来存储杨辉三角的每一行。
- 对于第一行和第二行,直接初始化。
- 从第三行开始,每一行的第一个和最后一个元素都是 1,中间的元素是上一行对应位置的两个元素之和。
- 遍历每一行,按照规则填充元素,直到生成numRows行。
#include <iostream>
#include <vector>
using namespace std;
class Solution {
public:
vector<vector<int>> generate(int numRows) {
vector<vector<int>> triangle;
if (numRows == 0) return triangle;
triangle.push_back({1});
if (numRows == 1) return triangle;
triangle.push_back({1, 1});
if (numRows == 2) return triangle;
for (int i = 2; i < numRows; i++) {
vector<int> row(i + 1, 1);
for (int j = 1; j < i; j++) {
row[j] = triangle[i - 1][j - 1] + triangle[i - 1][j];
}
triangle.push_back(row);
}
return triangle;
}
};
可以使用以下方式调用这个函数
int main() {
Solution solution;
int numRows = 5;
vector<vector<int>> triangle = solution.generate(numRows);
for (const auto& row : triangle) {
for (int num : row) {
cout << num << " ";
}
cout << endl;
}
return 0;
}
在这个代码中,首先判断输入的行数是否为 0、1 或 2,并进行相应的初始化。然后从第三行开始,逐行生成杨辉三角,直到生成指定的行数。在生成每一行时,利用上一行的元素来计算当前行的中间元素。最后,遍历生成的杨辉三角并输出每一行的元素。
2.只出现一次的数字I
给你一个整数数组 nums,其中恰好有两个元素只出现一次,其余所有元素均出现两次。 找出只出现一次的那两个元素。你可以按 任意顺序 返回答案。
你必须设计并实现线性时间复杂度的算法且仅使用常量额外空间来解决此问题。
思路:
- 首先计算整个数组中所有元素的异或结果。由于相同的数字异或为 0,所以最终的结果就是那两个只出现一次的数字的异或结果。
- 找到这个异或结果中任意一个为 1 的位。这一位为 1 意味着这两个只出现一次的数字在这一位上不同。
- 根据这个找到的位,将数组中的数字分为两组,一组在这个位上为 1,另一组在这个位上为 0。
- 分别对这两组数字进行异或操作,由于每组中除了那个只出现一次的数字外,其他数字都出现了两次,所以最终每组的异或结果就是那个只出现一次的数字。
#include <iostream>
#include <vector>
using namespace std;
class Solution {
public:
vector<int> singleNumber(vector<int>& nums) {
int xorResult = 0;
for (int num : nums) {
xorResult ^= num;
}
int diffBit = 1;
while ((xorResult & diffBit) == 0) {
diffBit <<= 1;
}
int num1 = 0, num2 = 0;
for (int num : nums) {
if (num & diffBit) {
num1 ^= num;
} else {
num2 ^= num;
}
}
return {num1, num2};
}
};
可以使用以下方式调用这个函数:
int main() {
Solution solution;
vector<int> nums = {1, 2, 1, 3, 2, 5};
vector<int> result = solution.singleNumber(nums);
cout << "两个只出现一次的数字是:" << result[0] << " 和 " << result[1] << endl;
return 0;
}
这个算法通过巧妙地利用异或操作的性质,在不使用额外的数据结构且线性时间复杂度的情况下找到了数组中两个只出现一次的数字。
3.只出现一次的数字II
给你一个整数数组 nums ,除某个元素仅出现 一次 外,其余每个元素都恰出现 三次 。请你找出并返回那个只出现了一次的元素。
你必须设计并实现线性时间复杂度的算法且使用常数级空间来解决此问题。
思路:
- 由于除了一个元素只出现一次外,其余元素都出现三次,考虑使用位运算来解决这个问题。
- 对于每一个整数的每一位,统计所有数字在该位上出现的次数。
- 如果某一位上的出现次数对 3 取余为 1,那么这个只出现一次的元素在该位上为 1,否则为 0。
#include <iostream>
#include <vector>
using namespace std;
class Solution {
public:
int singleNumber(vector<int>& nums) {
int ones = 0, twos = 0;
for (int num : nums) {
ones = (ones ^ num) & ~twos;
twos = (twos ^ num) & ~ones;
}
return ones;
}
};
可以使用以下方式调用这个函数:
int main() {
Solution solution;
vector<int> nums = {2,2,3,2};
int result = solution.singleNumber(nums);
cout << "只出现一次的数字是:" << result << endl;
return 0;
}
在这个算法中,使用了两个变量ones和twos来跟踪每一位上出现次数的状态。ones表示该位上出现一次的状态,twos表示该位上出现两次的状态。通过不断更新这两个状态,最终可以得到只出现一次的元素。
4.删除有序数组中的重复项
给你一个 非严格递增排列 的数组 nums ,请你 原地 删除重复出现的元素,使每个元素 只出现一次 ,返回删除后数组的新长度。元素的 相对顺序 应该保持 一致 。然后返回 nums 中唯一元素的个数。
考虑 nums 的唯一元素的数量为 k ,你需要做以下事情确保你的题解可以被通过:
更改数组 nums ,使 nums 的前 k 个元素包含唯一元素,并按照它们最初在 nums 中出现的顺序排列。nums 的其余元素与 nums 的大小不重要。
返回 k 。
思路
- 使用两个指针,一个指针 i 用于遍历数组,另一个指针 j 用于标记下一个不重复元素应该放置的位置。
- 遍历数组 nums,如果当前元素与前一个元素不同,说明找到了一个新的不重复元素,将其放置在 j 指向的位置,并将 j 向后移动一位。
- 遍历结束后,j 的值就是数组中不重复元素的个数。
#include <iostream>
#include <vector>
using namespace std;
class Solution {
public:
int removeDuplicates(vector<int>& nums) {
if (nums.empty()) return 0;
int j = 0;
for (int i = 1; i < nums.size(); i++) {
if (nums[i]!= nums[j]) {
j++;
nums[j] = nums[i];
}
}
return j + 1;
}
};
可以使用以下方式调用这个函数:
int main() {
Solution solution;
vector<int> nums = {1, 1, 2, 2, 3};
int k = solution.removeDuplicates(nums);
cout << "数组中唯一元素的个数为:" << k << endl;
cout << "处理后的数组为:";
for (int i = 0; i < k; i++) {
cout << nums[i] << " ";
}
cout << endl;
return 0;
}
这个算法通过一次遍历数组,高效地删除了重复元素,并返回了数组中唯一元素的个数。同时,它也满足了题目要求的原地修改数组,保持元素的相对顺序不变。
5.数组中出现次数超过一半的数字
给一个长度为 n 的数组,数组中有一个数字出现的次数超过数组长度的一半,请找出这个数字。
例如输入一个长度为9的数组[1,2,3,2,2,2,5,4,2]。由于数字2在数组中出现了5次,超过数组长度的一半,因此输出2。
保证数组输入非空,且保证有解
思路:
可以使用 “投票法” 来解决这个问题。
- 遍历数组,设置一个候选数字和一个计数变量。
- 初始时,候选数字可以设为数组的第一个数字,计数为 1。
- 遍历过程中,如果当前数字与候选数字相同,计数加 1;如果不同,计数减 1。
- 当计数为 0 时,更换候选数字为当前数字,并将计数重新设为 1。
- 最后得到的候选数字就是出现次数超过数组长度一半的数字。这是因为如果一个数字出现的次数超过一半,那么在遍历过程中它会 “抵消” 掉其他所有数字,最终留下来。
#include <iostream>
#include <vector>
using namespace std;
int findNumber(vector<int>& nums) {
int candidate = nums[0];
int count = 1;
for (int i = 1; i < nums.size(); i++) {
if (nums[i] == candidate) {
count++;
} else {
count--;
if (count == 0) {
candidate = nums[i];
count = 1;
}
}
}
return candidate;
}
可以使用以下方式调用这个函数:
int main() {
vector<int> nums = {1, 2, 3, 2, 2, 2, 5, 4, 2};
int result = findNumber(nums);
cout << "出现次数超过数组长度一半的数字是:" << result << endl;
return 0;
}
6.电话号码的字母组合
给定一个仅包含数字 2-9 的字符串,返回所有它能表示的字母组合。答案可以按 任意顺序 返回。
给出数字到字母的映射如下(与电话按键相同)。注意 1 不对应任何字母。
思路:
- 使用回溯法来解决这个问题。回溯法是一种通过穷举所有可能情况来找到所有解的算法。
- 首先定义一个映射表,将数字映射到对应的字母集合。
- 定义一个递归函数,函数接收当前的组合结果和下一个要处理的数字位置作为参数。
- 在递归函数中,如果已经处理到了字符串的末尾,说明找到了一个完整的字母组合,将其加入结果集合中。
- 如果还没有处理到字符串的末尾,获取当前位置的数字对应的字母集合,然后遍历这个集合,将每个字母加入当前组合结果中,并递归调用函数处理下一个位置。
- 最后返回所有找到的字母组合。
#include <iostream>
#include <vector>
#include <string>
using namespace std;
class Solution {
private:
const vector<string> keyboard = {"abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"};
void backtrack(string& digits, int index, string& combination, vector<string>& result) {
if (index == digits.length()) {
result.push_back(combination);
return;
}
int digit = digits[index] - '2';
for (char c : keyboard[digit]) {
combination.push_back(c);
backtrack(digits, index + 1, combination, result);
combination.pop_back();
}
}
public:
vector<string> letterCombinations(string digits) {
vector<string> result;
if (digits.empty()) return result;
string combination;
backtrack(digits, 0, combination, result);
return result;
}
};
可以使用以下方式调用这个函数:
int main() {
Solution solution;
string digits = "23";
vector<string> combinations = solution.letterCombinations(digits);
cout << "字母组合为:";
for (string combination : combinations) {
cout << combination << " ";
}
cout << endl;
return 0;
}
这个算法通过回溯法,逐步构建出所有可能的字母组合,对于给定的数字字符串,能够准确地返回所有对应的字母组合。
五、总结
vector的应用场景
1、数据存储:
适用于存储一组同类型的数据,如整数列表、字符串集合等。可以方便地进行添加、删除、访问和修改元素的操作。
2、动态数据结构:
在需要动态调整大小的场景中非常有用,比如在算法中存储中间结果、处理用户输入的动态数据等。
3、与其他库和算法的交互:
std::vector可以与 C++ 标准库中的其他组件(如算法、迭代器等)很好地配合使用。许多算法都接受std::vector作为输入或输出容器,使得代码更加简洁和高效。
4、总之,std::vector是 C++ 中一个功能强大、灵活且高效的容器类,广泛应用于各种编程场景中。它的动态大小调整、连续存储、类型安全和丰富的成员函数使得它成为处理数据集合的重要工具。