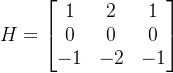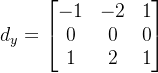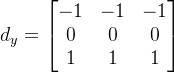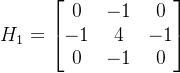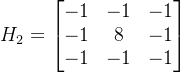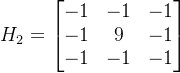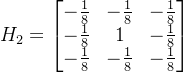关于图像锐化的一份介绍

在这篇文章中，我将介绍有关图像锐化有关的知识，具体包括锐化的简单介绍、一阶锐化与二阶锐化等方面内容。

一、锐化

1.1 概念

锐化（sharpening）就是指将图象中灰度差增大的方法，一次来增强物体的轮廓与边缘。因为发生锐化的地方都是发生灰度差突变的地方，所以锐化算法都是基于微分作用。

1.2 作用

一般来说，锐化增强灰度差，除了使物体与轮廓的细节增强后，它还是重要的预处理的一步，为了方便之后的物体检测与识别等。

二、一阶微分锐化方法

一阶微分锐化的计算公式十分简单，具体如下：

$f'(x,y)=\frac{\partial f}{\partial x}+\frac{\partial f}{\partial y}$

2.1 单方向一阶锐化

单方向的一阶锐化即是对某特定方向的边缘信息进行增强。通常，我们通过模板来实现，比如：

$H=\begin{bmatrix} 1 & 2 & 1\\ 0 & 0&0 \\ -1 &-2 &-1 \end{bmatrix}$

代码与处理后图像分别为：（代码中为了增强最后锐化后的效果，采用了垂直方向的锐化，而非上述模板中水平方向的锐化）

import cv2
import numpy as np
import matplotlib.pyplot as plt

image = cv2.imread(r'C:\Users\20349\Desktop\picture\tree.png')

# 定义单方向一阶微分锐化模板
kernel = np.array([[1, 0, -1],
                       [2, 0, -2],
                       [1, 0, -1]])

# 应用卷积核到图像上
sharpened_image = cv2.filter2D(image, -1, kernel)

image_rgb = cv2.cvtColor(image, cv2.COLOR_BGR2RGB)
sharpened_image_rgb = cv2.cvtColor(sharpened_image, cv2.COLOR_BGR2RGB)

fig, axes = plt.subplots(1, 2)

# 显示原图和处理后的图像
axes[0].imshow(image_rgb)
axes[0].set_title('Original Image')
axes[0].axis('off')  # 不显示坐标轴

axes[1].imshow(sharpened_image_rgb)
axes[1].set_title('Sharpened Image')
axes[1].axis('off')  # 不显示坐标轴

plt.show()

具体关于实现锐化部分的函数类似地可以写成代码如下：

def filter_2d(image, kernel):
    # 获取图像和卷积核的尺寸
    image_height, image_width, *image_channels = image.shape
    kernel_height, kernel_width = kernel.shape

    # 确保卷积核是奇数尺寸，以便有中心点
    if kernel_height % 2 == 0 or kernel_width % 2 == 0:
        raise ValueError("卷积核的宽高都应该是奇数")

    # 计算填充大小
    pad_size_height = kernel_height // 2
    pad_size_width = kernel_width // 2

    # 创建一个带有边框填充的图像副本，使用零填充
    padded_image = cv2.copyMakeBorder(image, pad_size_height, pad_size_height, pad_size_width, pad_size_width,
                                      cv2.BORDER_CONSTANT)

    # 如果图像是彩色图像，则需要分别处理每个通道
    if len(image_channels) > 0:
        channels = cv2.split(padded_image)
        output_channels = []
        for channel in channels:
            output_channel = np.zeros_like(channel)
            # 对于每个像素位置应用卷积
            for y in range(pad_size_height, image_height + pad_size_height):
                for x in range(pad_size_width, image_width + pad_size_width):
                    region = channel[y - pad_size_height:y + pad_size_height + 1,
                             x - pad_size_width:x + pad_size_width + 1]
                    output_channel[y - pad_size_height, x - pad_size_width] = (region * kernel).sum()
            output_channels.append(output_channel)
        output_image = cv2.merge(output_channels)
    else:
        # 对于灰度图像直接处理
        output_image = np.zeros_like(image)
        for y in range(pad_size_height, image_height + pad_size_height):
            for x in range(pad_size_width, image_width + pad_size_width):
                region = padded_image[y - pad_size_height:y + pad_size_height + 1,
                         x - pad_size_width:x + pad_size_width + 1]
                output_image[y - pad_size_height, x - pad_size_width] = (region * kernel).sum()

    return output_image

（该函数代码与实际调用的函数代码略有不同）

此外，在进行了上述步骤后进行取绝对值操作，可以增强对比度，避免负值影响问题等。

2.2 无方向一阶锐化

通过观察处理结果，我们发现单方向一阶微分锐化对于矩形特征的物体处理效果优秀，但对于不规则的物体处理效果有所欠缺，此时就需要无方向一阶微分锐化。

交叉微分锐化

首先是交叉微分锐化，其表达式为：

$g(i,j)=|f(i+1,j+1)-f(i,j)|+|f(i+1,j)-f(i,j+1)|$

该方法可以用代码表示为如下，以及其处理结果也如下所示：

def roberts_cross(image):
    image_height, image_width = image.shape

    output_image = np.zeros_like(image)

    # 定义Roberts算子
    kernel_x = np.array([[1, 0], [0, -1]])
    kernel_y = np.array([[0, -1], [1, 0]])

    # 对每个像素应用Roberts算子
    for y in range(0, image_height - 1):
        for x in range(0, image_width - 1):
            region = image[y:y + 2, x:x + 2]

            gradient_x = (region * kernel_x).sum()
            gradient_y = (region * kernel_y).sum()
            output_image[y, x] = np.sqrt(gradient_x ** 2 + gradient_y ** 2)

    # 归一化
    output_image = cv2.normalize(output_image, None, 0, 255, cv2.NORM_MINMAX)
    return output_image.astype(np.uint8)

Sobel锐化

关于Sobel锐化可以用表达式表示为：

$g(i,j)=(d^2 _x(i,j)+d^2 _y(i,j))^{\frac{1}{2}}$

其中：

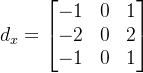
$d_x =\begin{bmatrix} -1 &0 &1 \\ -2&0 &2 \\ -1&0 &1 \end{bmatrix}$ $d_y = \begin{bmatrix} -1 & -2 &1 \\ 0&0 &0 \\ 1 &2 &1 \end{bmatrix}$

代码以及结果分别为：

def sobel_sharpen(image):
    image_float = image.astype(float)

    # 定义Sobel算子
    kernel_x = np.array([[-1, 0, 1], [-2, 0, 2], [-1, 0, 1]])
    kernel_y = np.array([[-1, -2, -1], [0, 0, 0], [1, 2, 1]])

    # 计算x方向和y方向的梯度
    gradient_x = cv2.filter2D(image_float, -1, kernel_x)
    gradient_y = cv2.filter2D(image_float, -1, kernel_y)

    # 合并两个方向的梯度
    gradient_magnitude = np.sqrt(gradient_x ** 2 + gradient_y ** 2)

    sharpened_image = image_float + gradient_magnitude

    sharpened_image = np.clip(sharpened_image, 0, 255)
    return sharpened_image.astype(np.uint8)

Prewitt锐化

如果将刚才的Sobel算法中核进行修改即可得到Prewitt算法，具体Prewitt算法的核为：

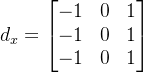
$d_x =\begin{bmatrix} -1 & 0 &1 \\ -1& 0& 1\\ -1& 0& 1 \end{bmatrix}$ $d_y = \begin{bmatrix} -1& -1 & -1\\ 0 & 0 &0 \\ 1& 1 &1 \end{bmatrix}$

其处理结果为：

三、二阶微分锐化方法

Laplacin算法

关于Laplacin算法的模板为：

$H_1 = \begin{bmatrix} 0 & -1 & 0\\ -1 & 4 &-1 \\ 0 & -1 & 0 \end{bmatrix}$

这个模板可以通过如下的表达式推导得出：

$\triangledown ^2 f = \frac{\partial ^2f}{\partial x^2}+\frac{\partial ^2f}{\partial y^2}$

（具体推导过程省略）

那么我们将这个模板用于锐化后得到结果为：

接着，我们为了增强最后Laplacian微分锐化的效果，我们可以对于刚才的模板进行修改，比如：

$H_2=\begin{bmatrix} -1 &-1 &-1 \\ -1 & 8 & -1\\ -1 & -1 & -1 \end{bmatrix}$

但要注意在修改这个模板时要注意配平，不然会出现问题。

刚才这个模板得到的结果如下：

为了展示效果，这里再提供一个未配平的模板，如下：

$H_2=\begin{bmatrix} -1 &-1 &-1 \\ -1 & 9 & -1\\ -1 & -1 & -1 \end{bmatrix}$

运用这个模板处理后的结果如下：（可以发现这个处理结果十分接近原图）

Wallis算法

如果对于刚才的这些模板中加入对数的处理，就可以得到Wallis算法，这种算法更接近人眼的视觉特性，得到的结果在暗区也可以很好处理，下面是一个模板举例：

$H_2=\begin{bmatrix} -\frac{1}{8} &-\frac{1}{8} &-\frac{1}{8} \\-\frac{1}{8}& 1 & -\frac{1}{8}\\ -\frac{1}{8}& -\frac{1}{8} & -\frac{1}{8} \end{bmatrix}$

处理结果如下：

此上