二叉树习题其二Java【力扣】【算法学习day.9】

前言

前言
书接上篇文章二叉树习题其一，这篇文章我们将基础拓展

###我做这类文档一个重要的目的还是给正在学习的大家提供方向（例如想要掌握基础用法，该刷哪些题？）我的解析也不会做的非常详细，只会提供思路和一些关键点，力扣上的大佬们的题解质量是非常非常高滴！！！

习题

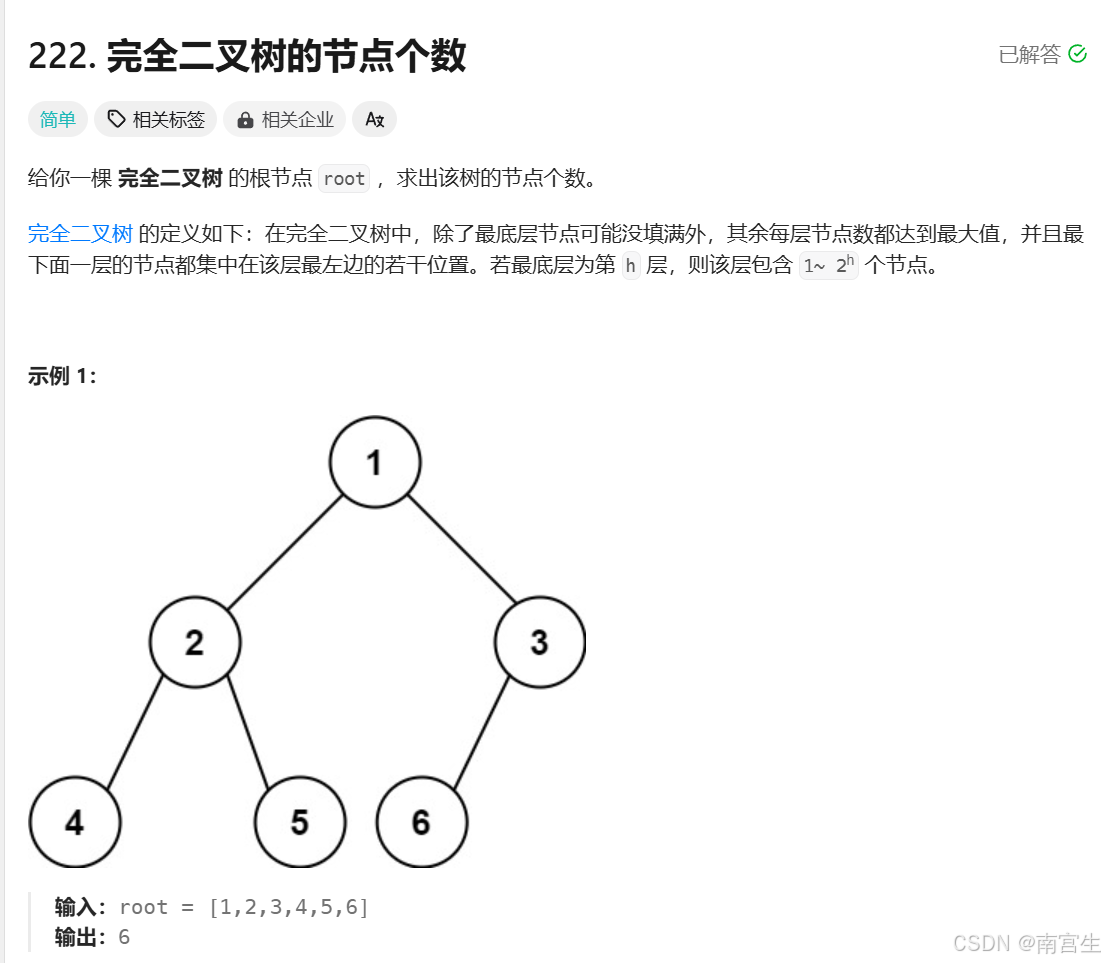
1.完全二叉树的节点个数

题目链接：222. 完全二叉树的节点个数 - 力扣（LeetCode）

题面：

基本分析：遍历二叉树，遍历的过程中维护一个变量用于统计节点个数

代码：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    int count = 0;
    public int countNodes(TreeNode root) {
        if(root==null)return 0;
        recursion(root);
        return count;
    }
    public void recursion(TreeNode node){
        if(node==null)return;
        if(node!=null)count++;
        recursion(node.left);
        recursion(node.right);
    }
}

2.平衡二叉树

题目链接：110. 平衡二叉树 - 力扣（LeetCode）

基本分析：判断是否是平衡二叉树就是判断每个‘根节点’的左右子树的高度差是否小于等于1，以此递归下去

代码：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public boolean isBalanced(TreeNode root) {
       return recursion(root)!=-1;
    }
    public int recursion(TreeNode node){
       if(node==null){
        return 0;
       }
       int left = recursion(node.left);
       if(left==-1){
        return -1;
       }
       int right = recursion(node.right);
        if(right==-1){
            return -1;
        }
       return Math.abs(left-right)>=2?-1:Math.max(left,right)+1;
    }
    
}

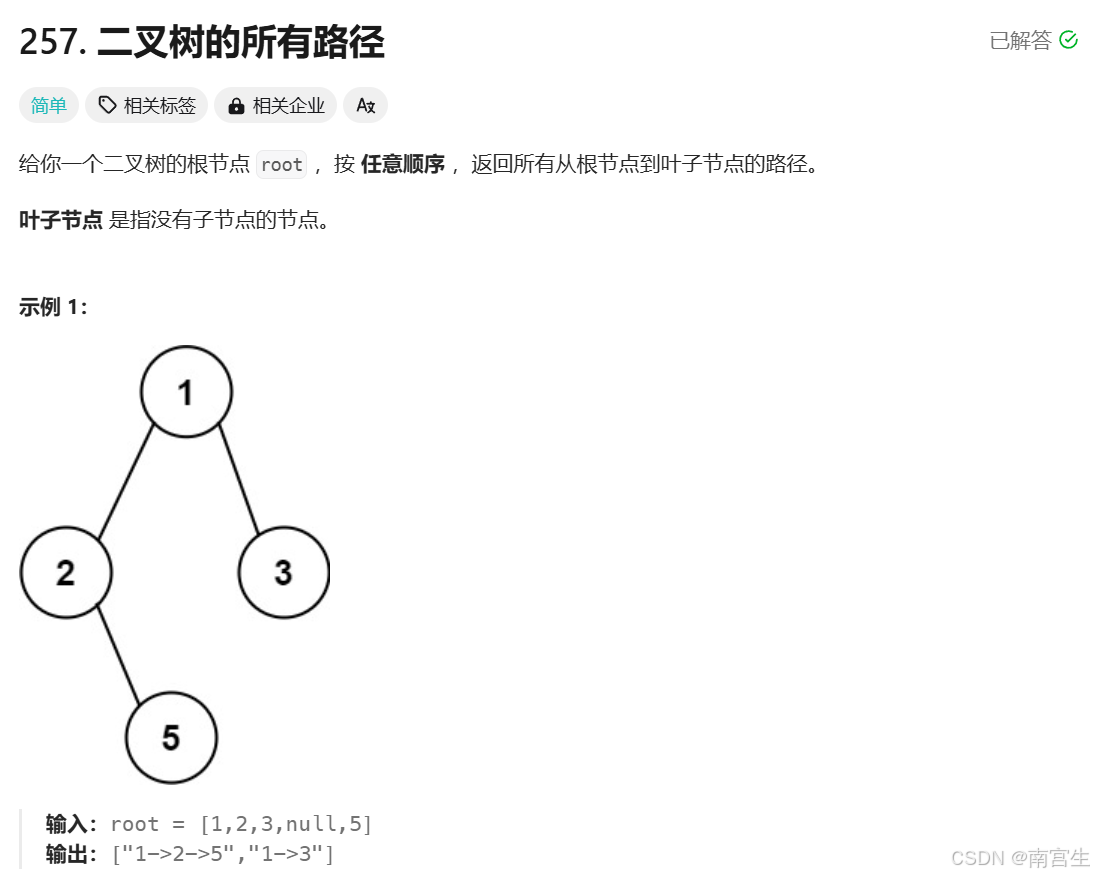
3.二叉树的所有路径

题目链接:257. 二叉树的所有路径 - 力扣（LeetCode）

基本分析：同样是遍历二叉树，值得注意的是，拼接箭头最好在递归函数调用的时候，这样可以省去很多麻烦

代码：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    List<String> list = new ArrayList<>();
    public List<String> binaryTreePaths(TreeNode root) {
        recursion(root,"");
        return list;
    }
    public void recursion(TreeNode node,String pre){
        pre+=node.val;
       if(node.left!=null) recursion(node.left,pre+"->");
       if(node.right!=null) recursion(node.right,pre+"->");
       if(node.left==null&&node.right==null){
        list.add(pre);
        return;
       }
    }
}

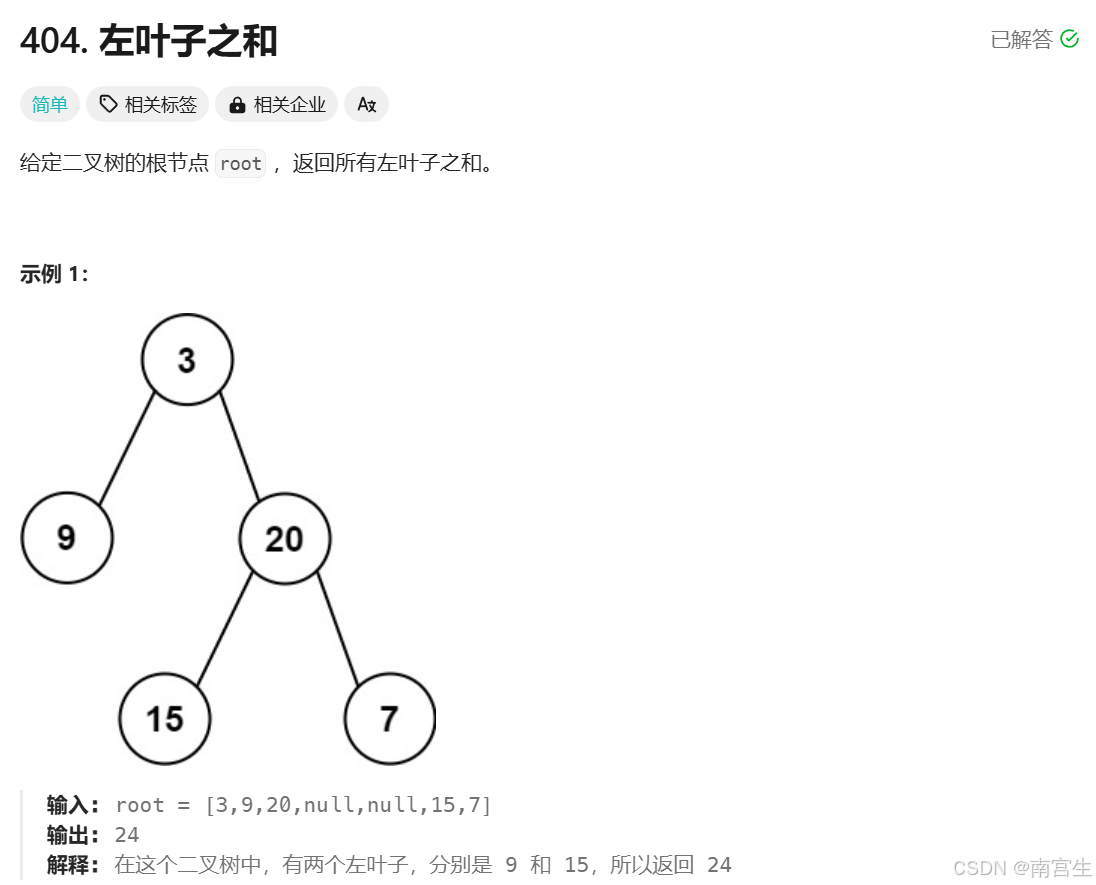
4.左叶子之和

题目链接:404. 左叶子之和 - 力扣（LeetCode）

基本分析：递归函数多维护一个字符串，用于标记该节点是否为左节点，然后就是遍历到最后一个节点进行相加操作

代码：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    int sum = 0;
    public int sumOfLeftLeaves(TreeNode root) {
        if(root==null||(root.left==null&&root.right==null))return 0;
        recursion(root.left,"left");
        recursion(root.right,"right");
        return sum;
    }
    public void recursion(TreeNode node,String flag){
        if(node==null){
            return;
        }
        if(node.left==null&&node.right==null&&flag.equals("left")){
            sum+=node.val;
        }
        if(node.left!=null){
           recursion(node.left,"left"); 
        }
        if(node.right!=null){
           recursion(node.right,"right"); 
        }
    }
}

5.找树左下角的值

题目链接:513. 找树左下角的值 - 力扣（LeetCode）

题面：

基本分析： 这道题要求是找最底层最左边的元素，如果我们调用递归函数是先遍历左节点再遍历右节点，那么一定是先遍历到最底层的左节点，所以只需要判断是不是更低一层即可，然后更改值

代码：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    int ans = 0;
    int count = Integer.MIN_VALUE;
    public int findBottomLeftValue(TreeNode root) {
        ans = root.val;
         recursion(root.left,2);
        recursion(root.right,2);
        return ans;
    }
    public void recursion(TreeNode node,int u){
        if(node==null)return;
        if(node.left==null&&node.right==null){
            if(u>count){
                System.out.println(1);
                count = u;
                ans = node.val;
            }
        }
        recursion(node.left,u+1);
        recursion(node.right,u+1);     
    }
}

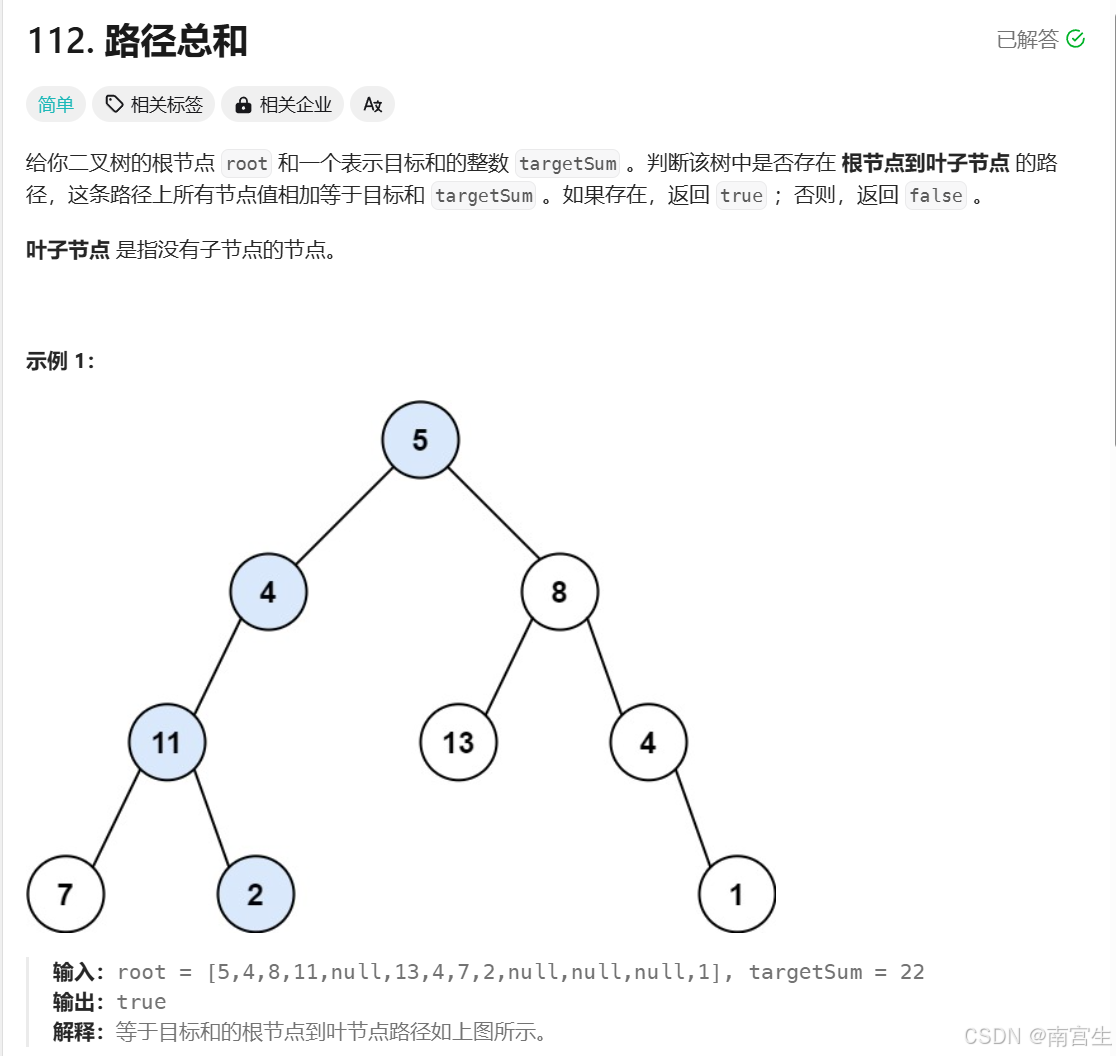
6.路径总和

题目链接:112. 路径总和 - 力扣（LeetCode）

题面：

基本分析： 遍历，并维护一个值，用来记录到达底部时是否和目标值相同

代码：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    int target =0;
    public boolean hasPathSum(TreeNode root, int targetSum) {
        if(root==null)return false;
        target = targetSum;
        return recursion(root,0);
    }
    public boolean recursion(TreeNode node,int sum){
        if(node==null)return false;
        sum+=node.val;
        if(node.left==null&&node.right==null){
            return sum==target;
        }
       boolean bool1 =  recursion(node.left,sum);
       boolean bool2 =  recursion(node.right,sum);
       return bool1||bool2;
    }
}

后言

上面是二叉树的部分习题，下一篇会讲解二叉树的其他相关力扣习题，希望有所帮助，一同进步，共勉！