一、密度聚类算法简介
密度聚类是一种数据挖掘和机器学习中常用的聚类算法,它能够发现具有类似密度的数据点,并将它们划分为不同的聚类。与传统的聚类算法(如K均值和层次聚类)相比,密度聚类不需要提前指定聚类的个数,能够自动发现数据中的不同密度区域,并将其归为一个簇。
二、密度聚类算法基本概念
MinPts:聚类最小点数;
聚类半径ε:在指定的聚类半径范围内,找到≥MinPts的点,则划分为一簇;
Ε邻域:给定对象半径为Ε内的区域称为该对象的Ε邻域; 核心点:在聚类半径范围内,能找到大于等于最小聚类点数个临近点,就称其为核心点。
边界点:若点的聚类半径邻域内包含的点数目小于MinPts,但是它在其他核心点的邻域内,则该点为边界点。
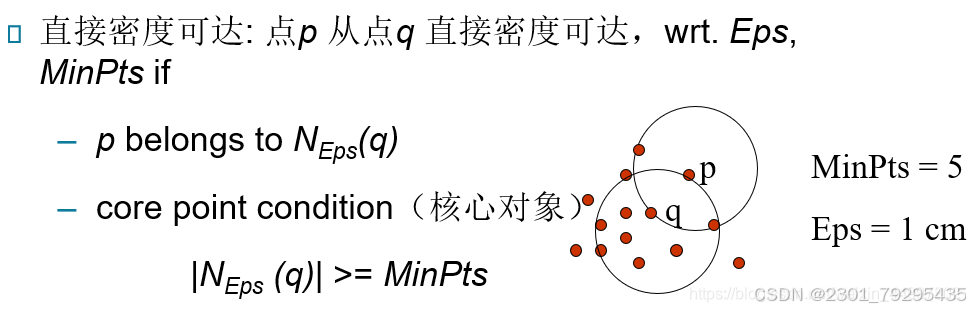
噪点(异常点):既不是核心点也不是边界点的点 。 直接密度可达:如果对象p是在对象q的ε-邻域内,而q是一个核心对象,我们就说对象p从对象q出发是直接密度可达的,如下图所示。
密度可达:如果存在一个对象链,
,对于
是从关于ε和m直接密度可达的,则对象p是从对象q关于ε和m密度可达的。
密度相连:如果对象集合中存在一个对象o,使得对象p和q是从o关于ε和m密度可达的,那么对象p和q是关于ε和m密度相连的。
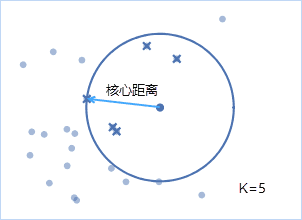
核心距离 :当前X点到其第k近的点的距离,k为指定的聚类最小点数,并表示为corek(x),若K=5,则核心距离如下图所示。
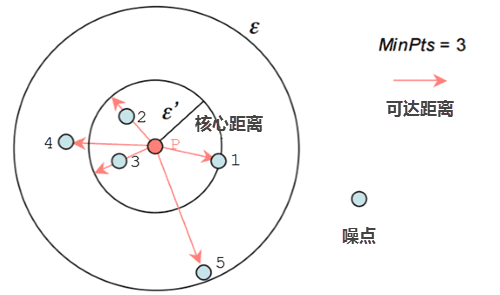
可达距离 :两点之间相互连通的距离与核心距离进行比较,如果两点距离小于核心距离,则核心距离作为两点的相互可达距离;如果两点距离大于核心距离,则两点距离为可达距离。
例如,下图中假设 minPts=3,聚类半径是 ε=d(P,5), P点 的核心距离是 d(P,1) , 点2到P点的距离小于核心距离,因此点2的可达距离是 核心距离 d(1,P) , 点3 的可达距离也是 核心距离 d(1,P) ,点4 到P点的距离大于核心距离,则点4的可达距离则是 d(4,P) 。
三、密度聚类算法基本思想
以每个数据点为圆心,聚类半径ε为半径画圆,然后数有多少点在这个圆内,这个数就是该点的密度值。然后我们可以选取一个密度阈值MinPts,如果圆内点数小于MinPts的点为低密度的点,而大于或等于MinPts的点为高密度的点(成为核心点Core Point)。如果有一个高密度的点在另一个高密度的点圆内,我们就把这两个点连接起来,这样我们就可以把很多点不断连接起来。之后,如果有低密度的点也在高密度的点的圆内,把它也连到最近的高密度点上,称之为边界点。这样所有能连到一起的点就形成了一个簇,而不在任何高密度点的低密度点就是异常点。
四、常用的密度聚类算法介绍
密度聚类算法有多种,以下介绍的密度聚类算法包括:密度聚类(DBSCAN)、层次密度聚类(HDBSCAN)和顺序密度聚类(OPTICS) 。
1、密度聚类(DBSCAN)
密度聚类是基于对象空间分布密度的一种聚类算法,将足够密度的区域划分为一簇,它将类簇定义为高密度相连点的最大集合。该算法对噪声点不敏感,噪声点的多少不影响聚类结果,并且能发现任意形状的类簇。
1)密度聚类(DBSCAN)算法流程
密度聚类根据指定的聚类半径,来查找紧密的聚类点和稀疏的噪声点,选择该聚类方式,需要设置聚类半径(即距离阈值ε)和点数据阀值m两个参数,具体实现步骤如下所示:
(1)从任意一个数据点开始,用距离阈值ε将这个点的邻域提取出来。
(2)如果在邻域内至少有m个点,那么该点是核心对象,被纳入第一个簇。否则该点将被标记为噪声(之后这个噪声点可能还是会变成簇中的一部分)。
(3)对于簇中的核心对象,在它邻域内的点也被纳入簇中。对于簇中所有点,再去提取它们的邻域,确定邻域内的点是否也属于当前的簇。
(4)第 2~3 步的过程会一直重复,直到簇内所有点都被确定,即所有在邻域内的点都被标记属于一个簇或者是噪声。
(5)一旦我们在当前簇做完这些操作,就会从新的数据点开始,接着发现下一个簇或噪声。这个过程反复进行直到所有的点都已被访问,最后每个点都被标记属于某一个簇或者是噪声。
2)聚类半径和点数据阀值设置
在密度聚类过程中,设置聚类半径(即距离阈值ε)和点数据阀值的值一般都是根据经验值来设定。如果对经验值聚类的结果不满意,可以适当调整聚类半径ε和 MinPts 的值,经过多次迭代计算对比,选择最合适的参数值。如果 MinPts 不变,聚类半径ε取得值过大,会导致大多数点都聚到同一个簇中,聚类半径ε过小,会导致一个簇的分裂;如果聚类半径ε 不变,MinPts 的值取得过大,会导致很多点将被标记为噪声点,MinPts 过小,会导致发现大量的核心点。
2、层次密度聚类(HDBSCAN)
层次密度聚类是根据指定的聚类最小点数,将不同密度的聚类点与稀疏噪点分离。层次聚类会以最佳方式创建最稳定聚类的聚类级别,该聚类会尽可能多的合并聚类点而不加入噪点。
层次密度聚类(HDBSCAN)是对DBSCAN算法的改进,引入了层次聚类的思想,对于聚类半径选择不当而导致聚类结果不佳的问题进行了纠正,降低了结果对参数的敏感度。
根据可变的距离及聚类点数目阀值,将不同密度的聚类点与稀疏噪点分离。选择该聚类方式,只需设置点数据阀值,具体分析步骤如下所示:
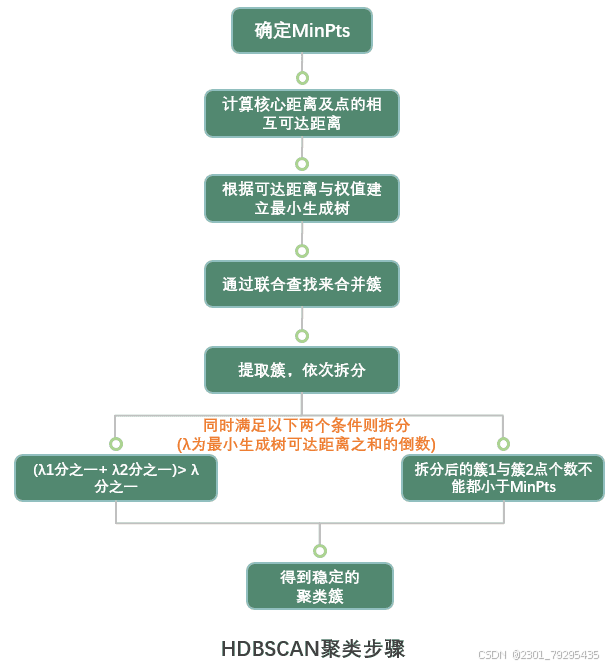
根据指定的MinPts,先计算点的核心距离以及相互可达距离,并构建最小生成树,通过联合查找将最小生成树进行连接合并,然后根据以下两个条件对最小生成树进行拆分,最终得到稳定性较好的聚类簇。
1、将一个最小生成树拆成两个簇,两个簇的可达距离之和分别为:λ1 和 λ2,若λ1 分之一加上 λ2分之一,大于原来的簇的可达距离之和λ分之一,则将该簇从此处打断划分为两个簇,依次重复。
2、若原始的簇划分为两个簇之后,每个簇的点个数都小于指定的 MinPts,则不再进行簇拆分。
层次密度聚类(HDBSCAN)的聚类步骤如下所示。
3、顺序密度聚类(OPTICS)
改善了 DBSCAN 的不足,使得聚类结果不会过于依赖 Eps 和 MinPts,结合相邻要素之间的紧密度,将不同密度的聚类点与噪点相分离,顺序密度聚类在优化检测到的聚类方面最灵活,但其属于计算密集型,尤其是当搜索距离较大时。
1)顺序密度聚类OPTICS算法流程
顺序密度聚类OPTICS根据相邻要素之间的距离和紧密度,将不同密度的聚类点与噪点相分离,选择该聚类方式,需设置聚类半径、点数据阀值、紧密度三个参数,其算法流程如下所示:
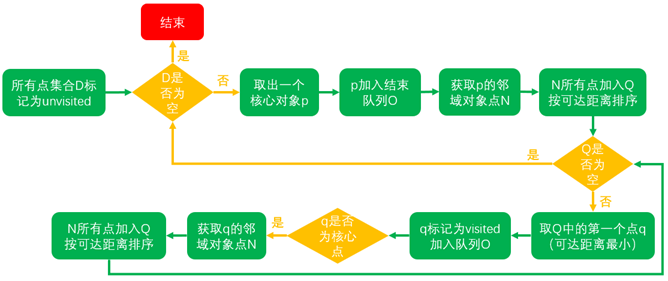
(1)已知数据集 D,创建两个队列,有序队列O和结果队列R(有序队列用来存储核心对象及其该核心对象的密度直达对象,并按可达距离升序排列;结果队列用来存储样本点的输出次序。可以把有序队列里面放的理解为待处理的数据,而结果队列里放的是已经处理完的数据)。
(2)如果D中所有点都处理完毕或者不存在核心点,则算法结束。否则,选择一个未处理(即不在结果队列R中)且为核心对象的样本点 p,首先将 p 放入结果队列R中,并从D中删除 p。然后找到 D 中 p 的所有密度直达样本点 x,计算 x 到 p 的可达距离,如果 x 不在有序队列 O 中,则将 x 以及可达距离放入 O 中,若 x 在 O 中,则如果 x 新的可达距离更小,则更新 x 的可达距离,最后对 O 中数据按可达距离从小到大重新排序。
(3)如果有序队列 O 为空,则回到步骤2,否则取出 O 中第一个样本点 y(即可达距离最小的样本点),放入 R 中,并从 D 和 O 中删除 y。如果 y 不是核心对象,则重复步骤 3(即找 O 中剩余数据可达距离最小的样本点);如果 y 是核心对象,则找到 y 在 D 中的所有密度直达样本点,并计算到 y 的可达距离,然后按照步骤2将所有 y 的密度直达样本点更新到 O 中。
(4)重复步骤2、3,直到算法结束。最终可以得到一个有序的输出结果,以及相应的可达距离。
上面的的描述可能让你听了云里雾里的,接下来我们以流程图的方式看下执行过程:
D: 待聚类的集合;
Q: 有序队列,元素按照可达距离排序,可达距离最小的在队首;
O: 结果队列,最后输出结果的点集的有序队列。
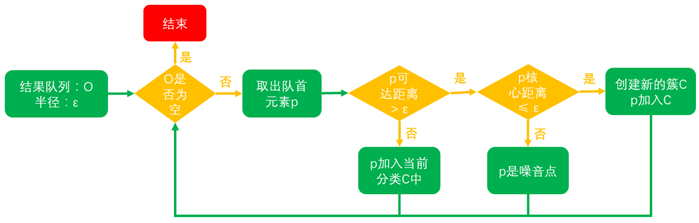
得到结果队列后,使用如下算法得到最终的聚类结果:
1)从结果队列中按顺序取出点,如果该点的可达距离不大于给定半径ε,则该点属于当前类别,否则至步骤2;
2)如果该点的核心距离大于给定半径ε,则该点为噪声,可以忽略,否则该点属于新的聚类,跳至步骤1;
3)结果队列遍历结束,则算法结束。
2)OPTICS邻域半径ε
OPTICS算法不是为了解决DBSACN的参数设置问题吗? 为什么算法中还需要输入参数ε和minPts?其实这里的ε和minPts只是起到算法辅助作用,也就是说ε和minPts的细微变化并不会影响到样本点的相对输出顺序,这对我们分析聚类结果是没有任何影响。
为什么说OPTICS算法对于ε不敏感,在算法参数上还要输入ε呢?
因为基于密度的聚类算法需要确定哪些点是核心点,哪些是躁点。所以为了这个目的,需要有个半径 ε。所以ε是必须给定的。
为什么当ε发生了变化,根据输出队列O还是可以得到新的分类?
在OPTICS算法中minPts并没有发生变化,虽然给定了ε,但最终得到的不是直接的分类结果,而是在这个ε和minPts下的有序队列,以及所有点的核心距离和可达距离。我们使用另外一个小的算法从队列中得到分类。简而言之:OPTICS算法通过给定一个ε值和minPts,计算出来的所有小于等于ε的情况的特征,最后利用这些特征,做一些简要的逻辑计算就可以得到分类。在对结果队列O的处理中,判断核心距离≤ε’这实则已经是在判断P是否为新半径ε’下的核心点了。所以ε发生了变化,核心点即使变化了也没关系,在O的处理中已经照顾到了,不是核心点的元素一定会被认定为躁点。保证了分类的正确性。
综上所述,OPTICS可以在minPts固定的前提下,对于任意的ε’ (其中ε’小于等于ε)都可以直接经过简单的计算得到新的聚类结果。