一、递归写法（dfs深搜）

1.1）思路讲解

1. 递归思想：
   • dfs(x)表示从第x家店开始的最大劫掠值。
   • 对每一家店铺，有两个选择：
     1. 不劫掠 当前店铺，即跳到下家 dfs(x+1)。
     2. 劫掠 当前店铺，且跳过下家（即跳到 dfs(x+2)），并加上当前店铺的价值 home[x]。
   • 返回这两者中的最大值，即 max(dfs(x + 1), dfs(x + 2) + home[x])。
2. 基础案例：
   • 当 x > n 时，返回0，表示没有店铺可劫掠。

缺点：

• 重复计算：对于相同的状态，dfs 可能会重复计算，从而导致性能低下，时间复杂度为 O(2^n)。

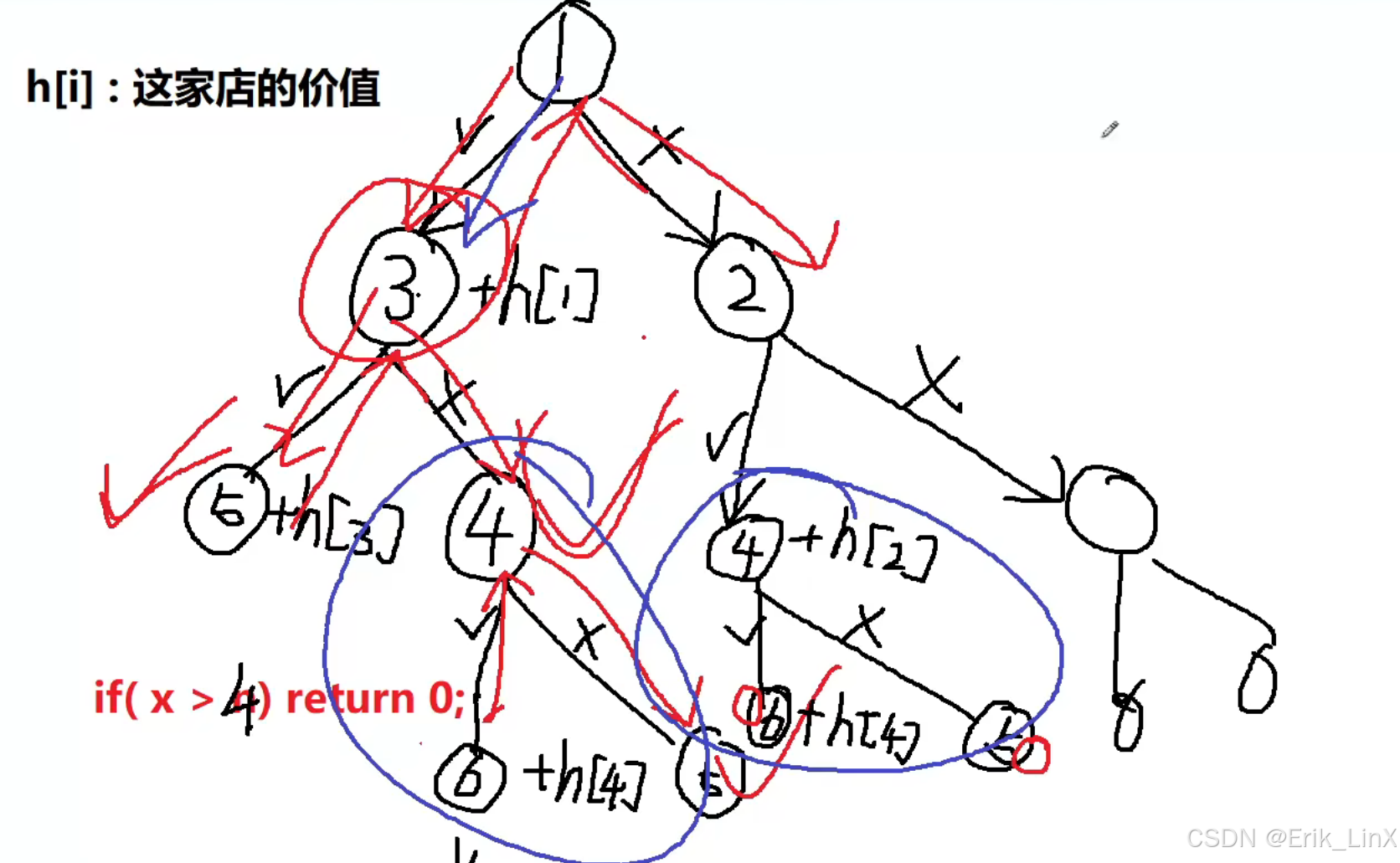
1.2）递归搜索树

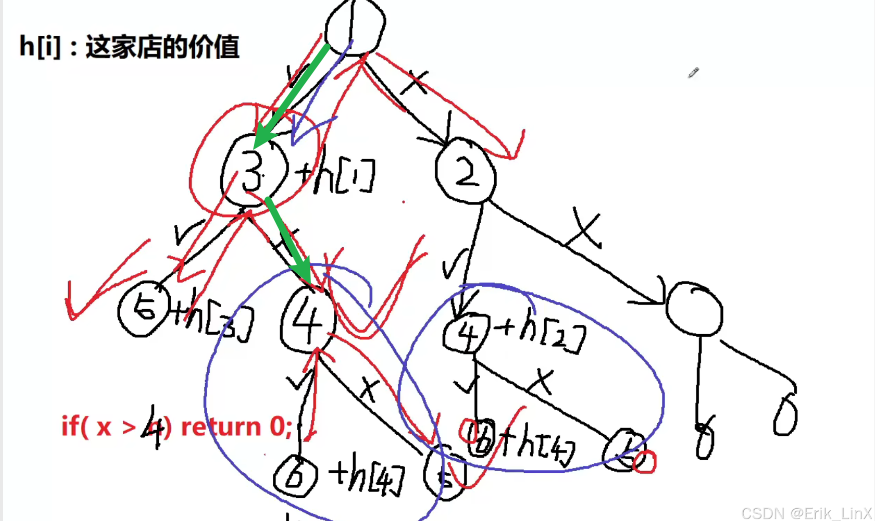
1.3）疑难点解析：[1][4]的洗劫

1、假设在这样的样例中，我们需要[1][4]才是最优情况，

2、我们可能会考虑，以上我们都是三家三家店铺的考虑，是否会漏掉这种情况呢？实际是不会的

3、因为会在图中的绿色情况达到情况，也就是([1]选择，[3]不选择，[4]选择)的情况下达成[1][4]的效果

1.4）代码解析

#include <bits/stdc++.h>
using namespace std;

typedef pair<int, int>PII;

const int N = 507;
int home[N],mem[N];
int n;

int dfs(int x)
{
    if (x > n) return 0;    

    return max(dfs(x + 1), dfs(x + 2) + home[x]);   //不选/选
}

void solve()
{
    memset(home, 0, sizeof(home)); //因为有多组测试样例，所以每一轮都需要初始化操作
     cin >> n;
    for (int i = 1; i <= n; i++)
    {
        cin >> home[i];
    }
    int res=dfs(1);
    cout << res << '\n';
}


int main()
{
    ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    int _ =1; cin >> _;
    while (_--) solve();

    system("pause");
    return 0;
}

二、记忆化搜索

2.1）思路讲解

• 对于已经计算过了的数据不做重复计算，如图中计算了两次店铺4的价值，造成了代码累赘，完全可以用一个记忆化数组mem来存储
• 由于没有return函数直接返回，所以需要用条件判断把语句关联在一起，防止越界

1. 记忆化搜索：

   • 我们在递归过程中使用了一个 mem 数组来记录已经计算过的状态。

   • 在递归之前，先检查 mem[x]是否已经计算过：

     • 如果计算过，直接返回 mem[x] 的值，避免重复计算。
     • 如果没有计算过，则继续递归计算，并将结果存入 mem[x]。

2. 优化效果

   • 通过缓存计算结果，减少了大量的重复计算，使得时间复杂度从 O(2^n) 降低到了 O(n)。

2.2）代码解析

#include <bits/stdc++.h>
using namespace std;

typedef pair<int, int>PII;

const int N = 507;
int home[N],mem[N];
int n;

int dfs(int x)
{
    if (mem[x]) return mem[x];  //记忆化搜索数组

    int sum = 0;

    if (x > n) sum=0;    //注意：由于没有return函数直接返回，所以需要用条件判断把语句关联在一起，防止越界
    else  sum=max(dfs(x + 1), dfs(x + 2) + home[x]);   //不选/选
    
    mem[x] = sum;
    return sum;
}

void solve()
{
    memset(home, 0, sizeof(home)); //因为有多组测试样例，所以每一轮都需要初始化操作
     cin >> n;
    for (int i = 1; i <= n; i++)
    {
        cin >> home[i];
    }
    int res=dfs(1);
    
    cout << res << '\n';
}


int main()
{
    ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    int _ =1; cin >> _;
    while (_--) solve();

    system("pause");
    return 0;
}

三、动态规划（dp）–>倒序

1.1）思路讲解

1. 动态规划：

   • 采用倒序遍历的方式，从后往前进行状态转移，逐步推导出每一家的最优劫掠方案。

   • 状态转移公式：

     dp[i] = max(dp[i + 1], dp[i + 2] + home[i])
     

     1. dp[i + 1]：表示不选择当前店铺，转移到下一个店铺。
     2. dp[i + 2] + home[i]：表示选择当前店铺，跳过下一个店铺，转移到第 i+2 家店铺。

2. 时间复杂度：

   • 时间复杂度为 O(n)，比递归方式更高效。

3. 空间复杂度：

   • 使用了一个 dp 数组，空间复杂度为 O(n)。

PS:应该于dfs的公式一致

• 由于到递归中，只有归的操作才是产生答案的操作，那么我们是否可以仅仅对归进行操作，从而得出答案呢？–>于是，dp产生了

• 相当于我们从边界往回进行倒序遍历，从已知推未知，所以应该是
  for (int i = n; i >= 1; i--)

• 注意:p[i]表示从n-i的最大店铺的值，所以应该输出dp[1]

1.2）代码解析

#include <bits/stdc++.h>
using namespace std;

typedef pair<int, int>PII;

const int N = 507;
int home[N],mem[N],dp[N];
int n;

int dfs(int x)
{
    if (mem[x]) return mem[x];  //记忆化搜索数组

    int sum = 0;

    if (x > n) sum=0;    //注意：由于没有return函数直接返回，所以需要用条件判断把语句关联在一起，防止越界
    else  sum=max(dfs(x + 1), dfs(x + 2) + home[x]);   //不选/选
    
    mem[x] = sum;
    return sum;
}

void solve()
{
    memset(home, 0, sizeof(home)); //因为有多组测试样例，所以每一轮都需要初始化操作
     cin >> n;
    for (int i = 1; i <= n; i++)
    {
        cin >> home[i];
    }
    for (int i = n; i >= 1; i--)
    {
        dp[i] = max(dp[i + 1], dp[i + 2] + home[i]);
    }
    cout << dp[1];  //表示从n-i的最大店铺的值，所以应该输出dp[1]
}


int main()
{
    ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    int _ =1; cin >> _;
    while (_--) solve();

    system("pause");
    return 0;
}

四、动态规划（正序）

4.1）思路讲解

1. 正序 DP：
   • dp[i] = max(dp[i - 1], dp[i - 2] + home[i]))：表示从前往后依次更新每一家的最优值。
   • 这个实现和倒序方法类似，只是状态更新的顺序不同。
2. 输出：
   • 输出的是 dp[n]，表示所有店铺经过劫掠后的最大总值。

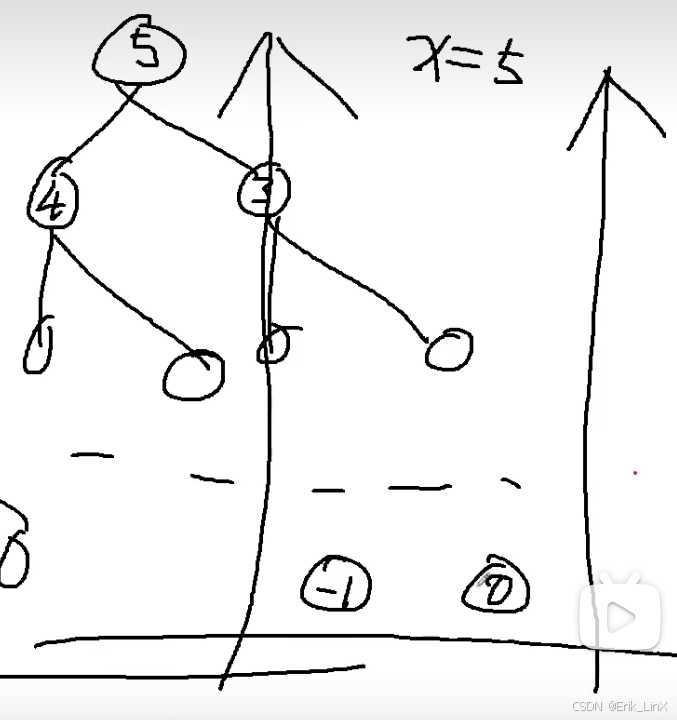
• 那么倒序看起来奇奇怪怪的，我们是否可以正序呢？？答案是肯定的，此时我们的搜索方向与原来的恰恰相反，也就是从n开始搜索
• 注意这道题还有一个映射的思想，因为i-2会使得数组下标越界

	for (int i = 1; i<=n; i++)
    {
        //dp[i] = max(dp[i - 1], dp[i - 2] + home[i]);
        dp[i+2] = max(dp[i+1], dp[i] + home[i]);
    }
    cout << dp[n+2];  //表示从1-n的最大店铺的值，所以应该输出dp[n]

• 注意答案也要同步映射！！

4.2）递归搜索树

4.3）代码解析：

#include <bits/stdc++.h>
using namespace std;

typedef pair<int, int>PII;

const int N = 507;
int home[N],mem[N],dp[N];
int n;

int dfs(int x)
{
    if (mem[x]) return mem[x];  //记忆化搜索数组

    int sum = 0;

    if (x > n) sum=0;    //注意：由于没有return函数直接返回，所以需要用条件判断把语句关联在一起，防止越界
    else  sum=max(dfs(x + 1), dfs(x + 2) + home[x]);   //不选/选
    
    mem[x] = sum;
    return sum;
}

void solve()
{
    memset(home, 0, sizeof(home)); //因为有多组测试样例，所以每一轮都需要初始化操作
     cin >> n;
    for (int i = 1; i <= n; i++)
    {
        cin >> home[i];
    }
    for (int i = 1; i<=n; i++)
    {
        //dp[i] = max(dp[i - 1], dp[i - 2] + home[i]);
        dp[i+2] = max(dp[i+1], dp[i] + home[i]);
    }
    cout << dp[n+2];  //表示从1-n的最大店铺的值，所以应该输出dp[n]
}


int main()
{
    ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    int _ =1; cin >> _;
    while (_--) solve();

    system("pause");
    return 0;
}
``