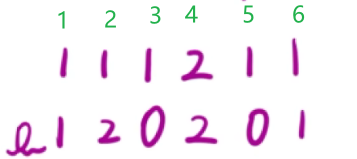一、题目：

二、思路讲解：

2.1：样例讲解

• 我们可以发现答案是如图所示得出的

a[1]+a[2]+a[3]=1+1+4=6
a[1]+a[2]+a[3]+a[4]+a[5]=1+1+4+5+1=12
a[2]+a[3]+a[4]+a[5]+a[6]=1+4+5+1+4=15
a[3]+a[4]=4+5=9
a[4]+a[5]=5+1=6

2.2：因此，我们可以考虑用前缀和来优化一下

1、因为我们只考虑某个数是否为k的倍数，所以可以对每个数压缩为%k

• 例如：a[2]=3 与 a[2]=0 对答案的影响一致
  
• 可以被优化为
  
• 对其进行前缀和且继续%k可以得到
  

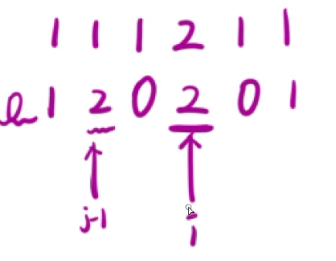
2.3：利用桶的思想简化操作

1、当我们走到一个位置i，此时，我们需要找到一段区间，以i为结尾，并且区间和会是$3$的倍数，我们可以发现：

• 此时，$pre[i]-pre[j-1]=0$，也就是说明，[3~4]这一区间和是三的倍数
  

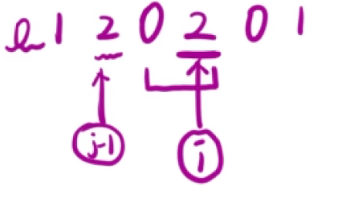
2、同样的，当$i=5$时，会出现如下情况：

• 此时可以发现[1~5] ， [3~5]同样符合条件
  

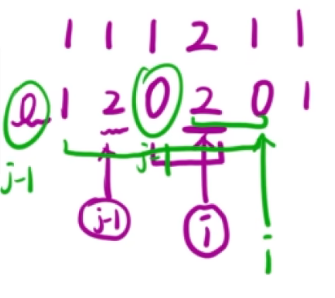
3、也就是说，我们每到一个位置，我们就往前找，和当前位置的值相同的点的数量，也就是符合条件的区间数

• 对于统计这个点之前有多少相同的值，我们可以使用桶的思想来简化操作
• 代码如下：

	ll res=0;
    //这里必须从0开始，否则会漏掉[1-i]的情况
    //比如 (pre[3]-pre[1])表示的是 a[2]+a[3],会漏掉1~3的情况
    for(int i=0;i<=n;i++)  
    {
        res+=cnt[prefix[i]]; //统计此前[1,i]出现了几次pre[i]

        cnt[prefix[i]]++;   //表示prefix[i]这种情况，往后多出现了一次
    }

• cnt[prefix[i]] 用来记录前缀和余数为 prefix[i] 的子数组出现的次数。
• 对于每个 prefix[i]，如果它之前已经出现过，那么当前的 prefix[i] 与之前的相同，会形成符合条件的子数组。所以每次遇到相同余数时，res 加上对应的计数。
• 然后更新 cnt[prefix[i]]，表示从 i 位置开始，prefix[i] 出现了一次。

也就是构建如下数组

可行性分析

• 前缀和的计算：每个 prefix[i] 都是通过前一个 prefix[i-1] 来计算的，且通过取余运算压缩到 [0, k-1] 范围。这使得所有的前缀和余数都在一个小的范围内（最多 k 种不同的余数）。
• 计数的有效性：cnt 数组是用来统计各个余数出现的次数。当 prefix[i] % k 相等时，说明有符合条件的子数组。你每次遍历时都更新 cnt[prefix[i]]，确保能正确地统计每个余数出现的次数。
• 边界情况：由于你从 i = 0 开始计算，并且 cnt[0] = 1 隐式初始化，因此可以正确地处理从数组开头到某个位置的子数组。例如，当 prefix[i] == 0 时，表示从 a[1] 到 a[i] 的和是 k 的倍数，这个情况会被正确计算在内。

3、完整代码

#include <bits/stdc++.h>
using namespace std;
using ll = long long;
const int N = 2e5 + 9;

ll a[N], cnt[N], prefix[N];

void solve()
{
   ll n,k;cin>>n>>k;
   for(int i=1;i<=n;i++) cin>>a[i];
    for(int i=1;i<=n;i++)   //前缀和数组
    {
        //因为我们只考虑是否为k的倍数，所以可以压缩为%k
        //比如：prefix[2]=3 与 prefix[2]=0 对答案的影响一致
        prefix[i]=(prefix[i-1]+a[i])%k; 
    }

    ll res=0;
    //这里必须从0开始，否则会漏掉[1-i]的情况
    //比如 (pre[3]-pre[1])表示的是 a[2]+a[3],会漏掉1~3的情况
    for(int i=0;i<=n;i++)  
    {
        res+=cnt[prefix[i]]; //统计此前[1,i]出现了几次pre[i]

        cnt[prefix[i]]++;   //表示prefix[i]这种情况，往后多出现了一次
    }
    cout<<res<<'\n';
}

int main()
{
   int t = 1;
   while(t --)solve();
   return 0;
}