导读
大家好,很高兴又和大家见面啦!!!
在上一篇内容中我们介绍了有符号整数的原码形式,有符号整数的原码表示法中,我们需要了解以下内容:
- 机器数最高位为符号位——0为正,1为负;
- 除最高位以外的二进制位为数值位
- 原码形式的取值范围: − ( 2 n − 1 − 1 ) ~ 2 n − 1 − 1 -(2^{n-1}-1)~2^{n-1}-1 −(2n−1−1)~2n−1−1
- 原码的真值0有两种形式: [ + 0 ] = 0 , 0000 [+0]=0,0000 [+0]=0,0000 与 [ − 0 ] = 1 , 0000 [-0]=1,0000 [−0]=1,0000
- 原码的运算过程过于复杂,不太适合直接使用原码进行运算
为了节约成本,,让有符号整数的运算变的简便,于是便有了补码的表现形式。下面我们就来认识一下有符号整数的补码;
一、补码
有符号整数在计算机中是以补码的形式进行存储,通过补码的形式,有符号整数的运算可以统一采用加法操作实现,这样即简化了操作,又节约了成本。
那什么是补码呢?
补码和原码一样,也是有符号整数的一种二进制表示形式。
1.1 原码转补码
对于有符号整数而言,补码的形式有两种:
- 正数的补码 = 正数的原码
- 正数9的原码: [ + 9 ] 原 = 0 , 1001 [+9]_原 = 0,1001 [+9]原=0,1001 其对应的补码 [ + 9 ] 补 = 0 , 1001 [+9]_补=0,1001 [+9]补=0,1001
- 负数的补码 = 正数的原码符号位不变,数值位按位取反,末位加1
- 负数9的原码: [ − 9 ] 原 = 1 , 1001 [- 9]_原 = 1,1001 [−9]原=1,1001
- 数值位按位取反得: [ − 9 ] 反 = 1 , 0110 [-9]_反 = 1,0110 [−9]反=1,0110
- 末位加1,得补码: [ − 9 ] 补 = 1 , 0111 [ -9]_补=1,0111 [−9]补=1,0111
真值0所对应的原码有两种形式,通过补码与真值的转换规则我们能够得到真值0的两种形式的补码:
- 正0的原码: [ + 0 ] 原 = 0 , 0000 [+0]_原 = 0,0000 [+0]原=0,0000 其对应的补码 [ + 0 ] 补 = 0 , 0000 [+0]_补=0,0000 [+0]补=0,0000
- 负数9的原码:
[
−
0
]
原
=
1
,
0000
[- 0]_原 = 1,0000
[−0]原=1,0000
- 数值位按位取反得: [ − 0 ] 反 = 1 , 1111 [-0]_反 = 1,1111 [−0]反=1,1111
- 末位加1,得补码: [ − 0 ] 补 = 0 , 0000 [ -0]_补=0,0000 [−0]补=0,0000
此时我们会发现,真值0的两种原码形式所对应的补码都是 [ 0 ] 补 = 0 , 0000 [ 0]_补=0,0000 [0]补=0,0000 。此时大家会不会想到什么?
有朋友已经反应过来了,既然真值0的补码只有1种形式,那么在机器数为8位的机器下 [ − x ] 补 = 1 , 0000000 [-x]_补 = 1,0000000 [−x]补=1,0000000 这个x是多少呢?
这里我们根据按权展开相加法可以得到: ( 1 , 0000 ) 2 = ( 128 ) 10 (1,0000)_2 = (128)_{10} (1,0000)2=(128)10 。从结果可以看到,这个 x x x 实际上表示的是真值 128 128 128,那也就是说 1 , 0000 1,0000 1,0000 其实就是真值 − 128 -128 −128 所对应的补码,因此我们便可以得到一个结论:
- 有符号整数的补码的取值范围: − 2 n − 1 ~ 2 n − 1 − 1 -2^{n-1}~2^{n-1}-1 −2n−1~2n−1−1
从取值范围来看,有符号整数的补码的范围要大于有符号整数的原码范围,所以有符号整数的原码可以直接转换成补码,但是有符号整数的补码不一定能够转换成原码。
那补码又应该如何转换成原码呢?
1.2 补码转原码
从原码转换成补码的过程来看,只要我们逆向推导就可以成功转化,即:
- 正数的原码 = 正数的补码
- 负数的原码 = 负数的补码末位减1后,再数值位按位取反
理论上来讲,这样的转换是没有任何问题的,但是在实际开发过程中,减法的实现成本太高,因此,在执行补码转换成原码时,实际上采取的是与原码转换成补码相同的方式:
- 正数的原码 = 正数的补码
- 负数的原码 = 负数的补码符号位不变,数值位按位取反,末位加1
这里我们主要以负9为例:
- − 9 -9 −9对应的原码: [ − 9 ] 原 = 1 , 1001 [-9]_原 = 1,1001 [−9]原=1,1001
- 符号位不变,数值位按位取反: 1 , 0110 1,0110 1,0110
- 末位加1: 1 , 0111 1,0111 1,0111
- − 9 -9 −9对应的补码: [ − 9 ] 补 = 1 , 0111 [-9]_补 = 1,0111 [−9]补=1,0111
- 符号位不变,数值位按位取反: 1 , 1000 1,1000 1,1000
- 末位加1: 1 , 1001 1,1001 1,1001
- − 9 -9 −9对应的原码: [ − 9 ] 原 = 1 , 1001 [-9]_原 = 1,1001 [−9]原=1,1001
可以看到补码通过同样的步骤,同样可以获得原码。因此原码与补码之间的相互转换规则可以总结为:
- 正数的原码 = 正数的补码
- 负数的原码与补码的转换都遵循:符号位不变,数值位按位取反,末位加1
二、反码
在有符号整数的表示方法中,原码在转换到补码时,正负数的规则是不一样的:
- 正数的补码 = 原码
- 负数的补码 = 原码符号位不变,数值位按位取反,末位加1
那现在问题来了,如果在转化的过程中,我们不做末位加1的操作,那得到的是什么呢?
其实,所得到的这个二进制形式我们将其称为反码。反码在计算机中主要是作为一个数码变换的中间表示形式。对于有符号整数的正数而言,它的反码与原码以及补码相同,而有符号整数的负数的反码是由原码直接将数值位按位取反获得。
因此,反码与原码一样,它所能表示的数值的取值范围: − ( 2 n − 1 − 1 ) ~ 2 n − 1 − 1 -(2^{n-1}-1)~2^{n-1}-1 −(2n−1−1)~2n−1−1 ,并且在反码中真值0的表示也有两种形式:
- 正0的反码: [ + 0 ] 反 = 0 , 0000 [+0]_反=0,0000 [+0]反=0,0000
- 负0的反码: [ − 0 ] 反 = 1 , 1111 [-0]_反=1,1111 [−0]反=1,1111
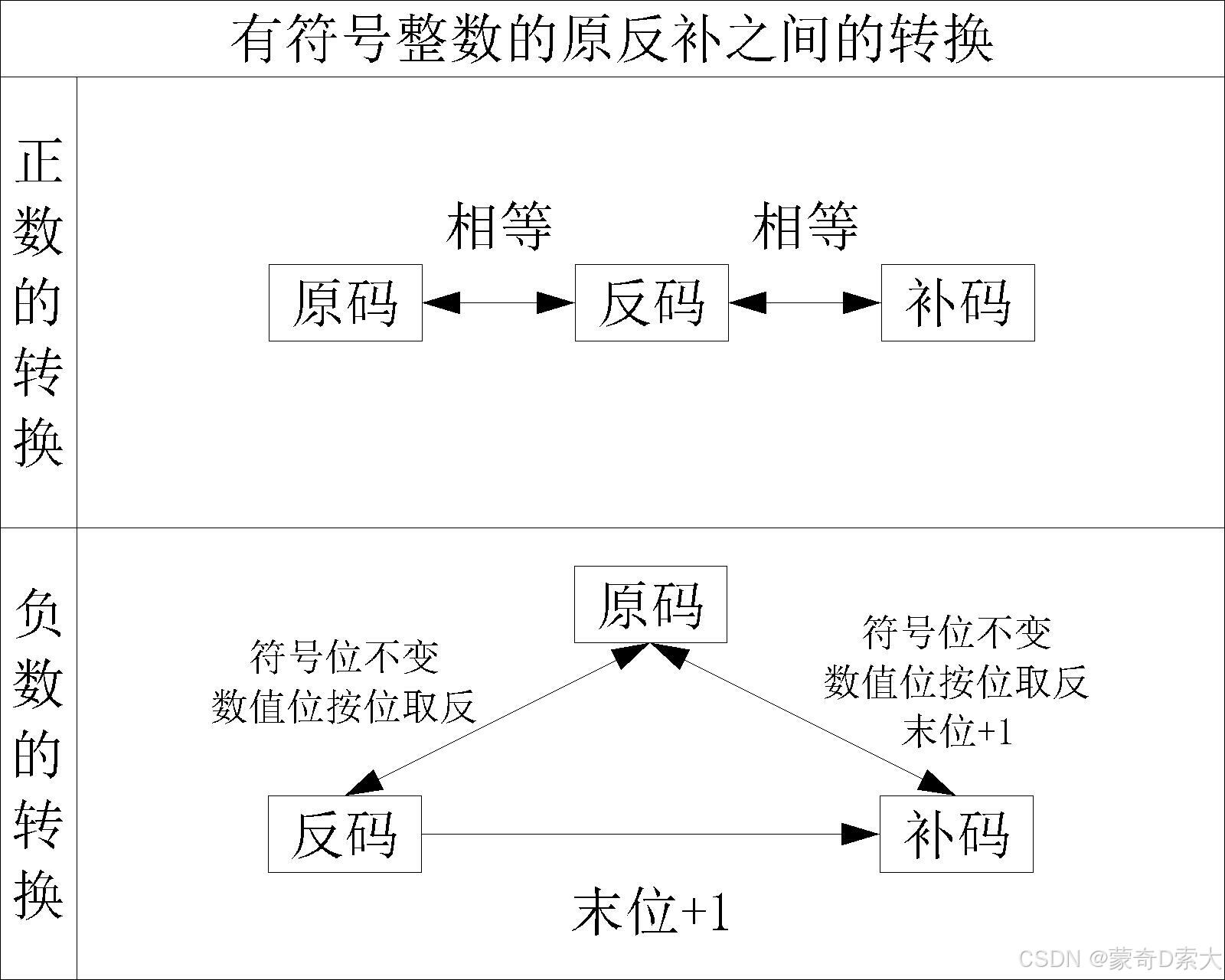
三、原码、补码、反码的相互转换
前面我们已经介绍了原码与补码之间的转换规则,那么反码与原码和补码又是如何进行转换的呢?
从反码的定义来看:
- 正数的反码 = 正数的原码
- 负数的反码 = 负数原码的符号为不变,数值位按位取反
那也就是说,反码与原码之间的转换的规则遵循:
- 正数的反码 = 正数的原码
- 负数的原码与反码的转换:符号位不变了,数值位按位取反
这么看来,对于有符号正数而言,其原码、反码与补码就是相同的,即:
[
x
]
原
=
[
x
]
反
=
[
x
]
补
,
x
>
=
0
[x]_原=[x]_反=[x]_补,x >= 0
[x]原=[x]反=[x]补,x>=0
而对于负数而言,它们之间的关系则稍有不同。从理论上来说,负数的原反补之间满足关系:
- 原码与反码:符号位不变,数值位按位取反
- [ x ] 补 = [ x ] 反 + 1 [x]_补 = [x]_反 + 1 [x]补=[x]反+1
- [ x ] 反 = [ x ] 补 − 1 [x]_反 = [x]_补- 1 [x]反=[x]补−1
但是在硬件实现的过程中,补码是无法直接转换成反码的,只能通过原码来得到反码,即:
- 补码—>原码—>反码
- 补码符号位不变,数值位按位取反,末位加1得原码
- 原码符号位不变,数值位按位取反得反码
因此有符号整数的原码、反码与补码之间的转换关系为:
但是需要注意的是,补码中负值的取值范围要比原码多一个 − 2 n − 1 -2^{n-1} −2n−1 ,以机器数为8位的机器为例,按照补码转原码的规则来看,其对应的转换过程为:
//-128补码转原码
符号位 数值位
1 000 0000 // -128补码
按位取反: // -128补码
-------------------------
1 111 1111 // 数值位按位取反
+ 1 // 末位加1
-------------------------
1 000 0000 // 原码
这里我们需要注意的是,在原码中,符号位是不参与运算的,因此 − 128 -128 −128 的补码没有对应的原码,这个点一定要注意,所有的原码都有一一对应的补码,但是并不是所以的补码都有一一对应的原码。
结语
今天的内容到这里就全部结束了,在下一篇内容中我们将介绍《有符号整数的运算》的相关内容,大家记得关注哦!如果大家喜欢博主的内容,可以点赞、收藏加评论支持一下博主,当然也可以将博主的内容转发给你身边需要的朋友。最后感谢各位朋友的支持,咱们下一篇再见!!!