导读

大家好，很高兴又和大家见面啦！！！

今天我们将会开始咱们编程学习过程中的一个非常重要的内容学习——算法（algorithm）。

说到算法，相比大家应该不会陌生了，在【数据结构】专栏的绪论部分中，我们就有介绍过算法的定义：

算法（Algorithm）是对特定问题求解步骤的一种描述，它是指令的有限序列，其中的每条指令表示一个或多个操作。

但是定义归定义，那究竟什么是算法，我相信大家在学习的过程中或多或少都有问过自己，并且大家得到的回答大多数都是——动态规划、贪心、分治……这些才是算法。

那事实是不是这样呢？在今天的内容中，我将会给大家介绍我自己对算法的一个独特的理解（至少在我目前看来）。希望阅读本文的各位能够通过今天的内容对算法有一个更加深刻的认识；

一、算法

1.1 什么是算法？

要理解算法，我们还是得从其定义出发——对特定问题求解步骤的一种描述。怎么来理解这个定义呢？下面我来借助几道题，大家就应该能够明白了：

1. BC1 Hello Nowcoder：输出"Hello Nowcoder!"。开始你的编程之旅吧。
2. 2235. 两整数相加：给你两个整数 num1 和 num2，返回这两个整数的和。
3. 94. 二叉树的中序遍历：给定一个二叉树的根节点 root ，返回 它的 中序 遍历 。

这几道题想必大家应该都不陌生了吧，没错，这些都是牛客网和力扣网上的题目。如果没有见过这些题目的朋友可以点击链接来尝试着解答一些这些题或者跟我一起来解决上述的三道题；

1.2 例题求解

上述例举的三道题目都是我们学习编程语言和数据结构的过程中会遇到的最基础最简单的题目，它们各自的解题方法也是十分的简单，如下所示：

//1.[BC1 Hello Nowcoder]——简单输出——入门
//输出"Hello Nowcoder!"。开始你的编程之旅吧。
//输入描述：
//无
//输出描述：
//Hello Nowcoder!
#include <stdio.h>

int main() {
    printf("Hello Nowcoder!");
    return 0;
}

这一题是牛客网上在线编程中基础语法的一道入门题，我们只需要通过调用printf函数对需要输出的内容进行输出即可，题目比较基础，因此很容易就能通过这道题：

//2.[2235. 两整数相加]——数学——简单
//给你两个整数 num1 和 num2，返回这两个整数的和。
//示例 1：
//输入：num1 = 12, num2 = 5
//输出：17
//解释：num1 是 12，num2 是 5 ，它们的和是 12 + 5 = 17 ，因此返回 17 。
//示例 2：
//输入：num1 = -10, num2 = 4
//输出： - 6
//解释：num1 + num2 = -6 ，因此返回 - 6 。
//提示：
//- 100 <= num1, num2 <= 100

#include <stdio.h>
int sum(int num1, int num2) {
    return num1 + num2;
}

int main() {
    int a = 0, b = 0;
    while (scanf("%d%d", &a, &b) == 2) {
        int ret = sum(a, b);
        printf("%d\n", ret);
    }
    return 0;
}

这一题是力扣网上的一道数学简单题，我们只需要借助操作符'+'，将函数的形参进行相加，并将结果返回即可，通过也是十分容易的：

这里有朋友可能会奇怪，为什么我们在力扣网中没有写main函数，但是在上述我给出的代码中却有main函数？

这是因为在力扣网中的题目与牛客网不一样，力扣网中的题目是以函数接口的形式给出，即，力扣网的系统在进行检测时，是直接调用的该函数接口完成检测，因此我们如果在自己的IDE上进行调试运行时，就需要自己来编写main函数的内容。

大家可以直接把上述代码复制到自己的IDE中进行测试。这里我需要简单的解释一下，我们在main函数中通过循环语句，并将输入的返回值作为循环的判断语句，实现了多组输入的功能，因此只要我们输入的是2个整数，那我们就可以一直进行测试，倘若有一个不是整数，那么程序就会结束。

//3.[94. 二叉树的中序遍历]——栈、树、深度优先搜索、二叉树——简单
//给定一个二叉树的根节点 root ，返回 它的 中序 遍历 。
//示例 1：
//输入：root = [1, null, 2, 3]
//输出：[1, 3, 2]
//示例 2：
//输入：root = []
//输出：[]
//示例 3：
//输入：root = [1]
//输出：[1]
//提示：
//树中节点数目在范围[0, 100] 内
//- 100 <= Node.val <= 100
//进阶: 递归算法很简单，你可以通过迭代算法完成吗？
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
struct TreeNode {
    int val;
    struct TreeNode* left;
    struct TreeNode* right;
};
/**
 * Note: The returned array must be malloced, assume caller calls free().
 */
void visit(struct TreeNode* root, int* a, int i) {
    a[i] = root->val;
}
void InOrder(struct TreeNode* root, int* a, int* pi) {
    if (!root)
        return;
    InOrder(root->left, a, pi);
    visit(root, a, *pi);
    *pi += 1;
    InOrder(root->right, a, pi);
}
int BTSize(struct TreeNode* root) {
    if (!root)
        return 0;
    int left = BTSize(root->left) + 1;
    int right = BTSize(root->right) + 1;
    return left + right;
}
int* inorderTraversal(struct TreeNode* root, int* returnSize) {
    *returnSize = 0;
    if (!root) {
        return NULL;
    }
    int size = BTSize(root);
    int* ans = (int*)calloc(size, sizeof(int));
    assert(ans);
    InOrder(root, ans, returnSize);
    return ans;
}

这一题对于已经学到了【数据结构——二叉树】的朋友来说应该是非常简单的，还没学到的朋友也不要着急，我们先简单的了解一下该题的解题思路：

• 首先我们需要知道二叉树的4种遍历方式：
  • 先序遍历（先根遍历）：根结点—>左子树—>右子树
  • 中序遍历（中根遍历）：左子树—>根结点—>右子树
  • 后序遍历（后根遍历）：左子树—>右子树—>根结点
  • 层序遍历：从根结点开始，从上往下，从左往右，依次访问每一层的结点
• 之后我们可以通过上述任意一种遍历的方式来获取该二叉树的结点数，通过该结点数来申请需要返回的数组空间。

在上述代码中我选择的是后序遍历的方式来计算结点数，即返回值的组成为：
$$左子树+右子树+根结点$$

• 叶子结点的返回值：0 + 0 + 1
• 非叶子结点的返回值：左子树 + 右子树 + 1

这里的1就代表的根结点的数量，每一棵子树的根结点都有且仅有1个。

• 最后我们通过中序遍历的方式依次访问二叉树的各个结点，并将结果存储在返回的数组中即可

整个的解题思路以及代码的编写还是非常简单的，所以通过这道题也是非常轻松的：

二叉树拓展

如果有朋友想要在自己的IDE中来对上述代码进行测试，我们应该如何进行呢？

这个问题也并不难，我们只需要自己创建一颗题目所给的二叉树即可，但是由于题目所给的二叉树不一定是一颗完全二叉树，因此我们自己在测试前，需要将题目所给的二叉树画出来，并将其转换为完全二叉树才能进行测试。创建二叉树的代码如下所示：

void Creat(struct TreeNode** root, int* a, int len, int* pi) {
    if (!root)
        return;
    if (*pi < len && a[*pi] >= -100 && a[*pi] <= 100) {
        //为结点申请空间
        *root = (struct TreeNode*)calloc(1, sizeof(struct TreeNode));
        assert(root);
        (*root)->left = NULL;
        (*root)->right = NULL;
        (*root)->val = a[*pi];
        *pi += 1;
        //创建左子树
        Creat(&((*root)->left), a, len, pi);
        //创建右子树
        Creat(&((*root)->right), a, len, pi);
    }
    else {
        *pi += 1;
    }
}
void Print(int* a, int len) {
    printf("[");
    for (int i = 0; i < len; i++) {
        if (i == len - 1) {
            printf("%d", a[i]);
        }
        else {
            printf("%d, ", a[i]);
        }
    }
    printf("]\n");
}
int main() {
    int tree[100] = { 0 };
    int size = 0;
    while (scanf("%d", &size) == 1) {
        for (int i = 0; i < size; i++) {
            //空节点输入值101，非空结点输入-100—100
            scanf("%d", &tree[i]);
        }
        struct TreeNode* root = NULL;
        int i = 0;
        Creat(&root, tree, size, &i);
        int len = 0;
        int* ret = inorderTraversal(root, &len);
        Print(ret, len);
        free(ret);
        ret = NULL;
    }
    return 0;
}

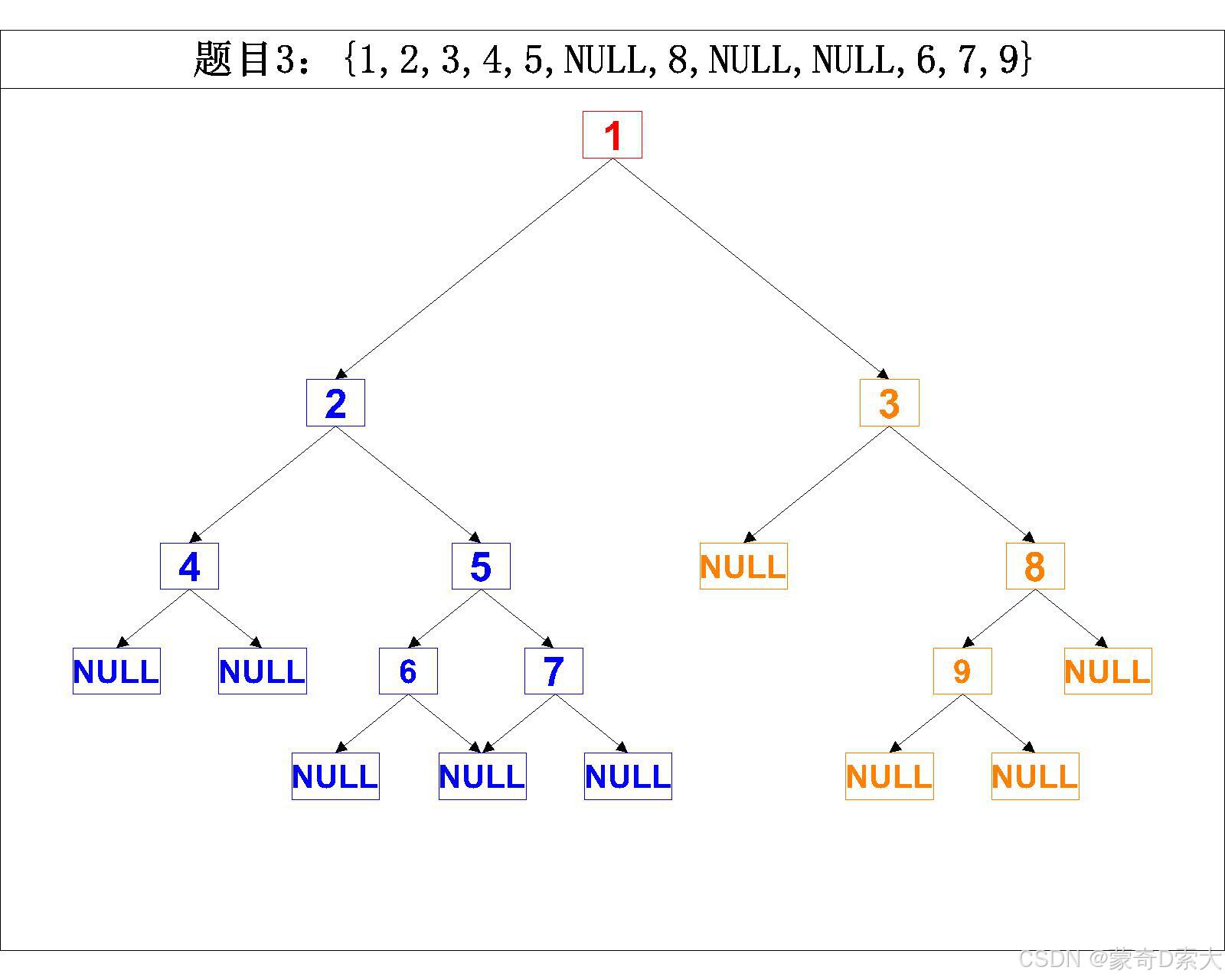
这里我们以例子：root = [1,2,3,4,5,null,8,null,null,6,7,9]为例，该用例所对应的二叉树应该是：

其对应的中序遍历的结果应该是：[4,2,6,5,7,1,3,9,8]

当我们要在自己的IDE通过上述代码来进行验证时，我们应该输入的内容为：

size = 19
tree[100] = {1,2,4,101,101,5,6,101,101,7,101,101,3,101,8,9,101,101,101};

这样我们输出的结果才是：[4,2,6,5,7,1,3,9,8]

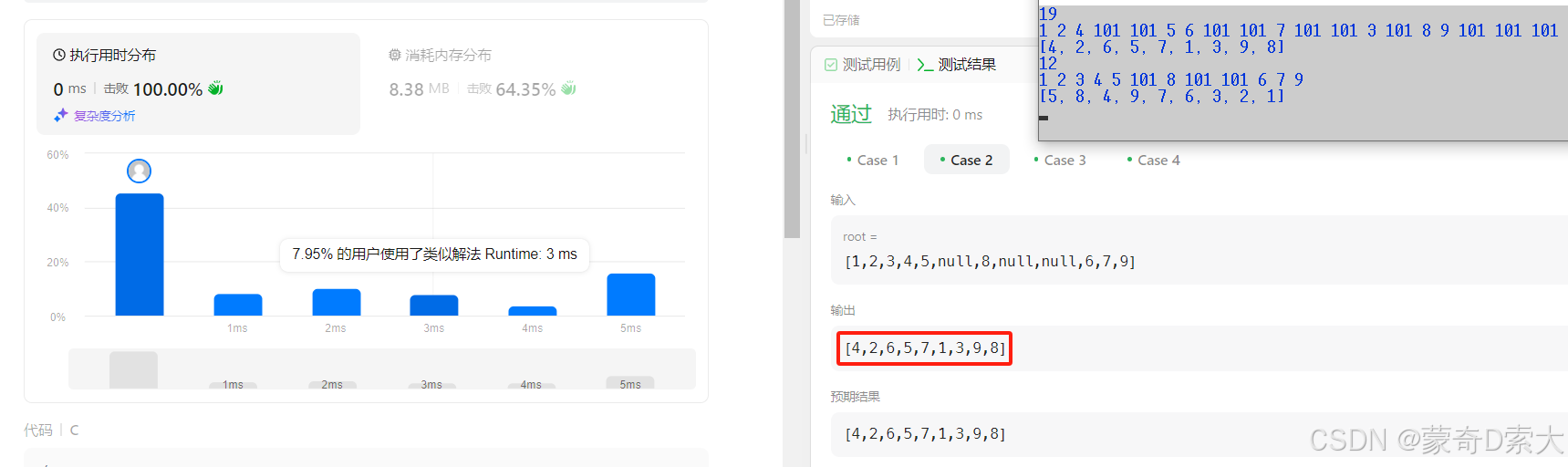
如果我们直接按照 root = [1,2,3,4,5,null,8,null,null,6,7,9] 该用例进行输入，则我们会得到一个错误的结果，如下所示：

因此我们在自己的IDE中进行代码测试时，一定要注意输入的用例必须是完全二叉树。当然，上述的用例中对于后面的3个空结点，我们是可以省略的，即，我们也可以输入：

size = 16
tree[100] = {1,2,4,101,101,5,6,101,101,7,101,101,3,101,8,9};

这个是不影响最终的结果的，这里的测试结果我就不再展示，大家可以在自己的IDE中进行验证。

这里的每一道题，都是一个特定的问题，而算法就是描述解决这些问题的求解步骤的。换句话说，能够解决这些问题的求解步骤也就是我们所说的算法。

1.3 个人对算法的理解

现在就有朋友可能会反驳我了，你这些题目都是些啥呀，又没有什么实际意义，所以解决这些题目的步骤是不能够被称为算法的。那些能被称为算法的只有什么动态规划呀、深度优先搜索呀、贪心呀、分治呀……这些能够解决实际问题的才能称得上是算法。

我相信有上述这个想法的朋友应该是占大多数的，还有少部分朋友是压根就不知道什么是算法。这里我给出的解释是上述的这个想法是正确的，但也错误的。

正确的地方就在于，我们现在所说的算法是特指的这些能叫得出名字的，十分高大上的求解步骤，错误的地方就在于，我们不能将这个认知放在整个编程学习的过程中。

这里我将上述的观点称之为狭义的算法，而我现在介绍的观点是基于定义出发的广义的算法。接下来我就来给大家解释一下，为什么我会有这样的想法；

1.4 个人观点的由来

我之所以会有广义算法和狭义算法的想法，其根本原因就是两个字——简化。这里的简化是要简化什么呢？

我作为一个跨专业零基础开始自学【C语言】的编程小白，我在学习的阶段遇到的一个最大的难题就是两个字——理解。我需要理解计算机这个专业的各种我之前从未见过的名词以及含义，我需要理解编程语言的各种语法以及使用方式，我需要理解各个库函数的功能以及使用……因此，为了能够更快的上手编程语言，为了更快的吸收计算机的各类知识，我就需要将这些复杂的问题给简化。

和大家一样，我在开始学习算法时，我看的课程中以及平时跟博客的小伙伴们交流的过程中，不管是上课的老师还是小伙伴们，大家对算法都是认为是只有那些叫得上名字的才能叫做算法，而像第一题这种只是简单的调用库函数或者第二题这种使用操作符的解题方式，只能够称得上是计算机编程。

正因为这样，绝大多数人都会和我刚开始一样，将算法和编程给割裂开来，然后就会产生一种错觉，编程是一件很简单的事情，而算法则是一件很难的事情。正是这种想法的出现，我们才会主动的在自己学习算法的过程中给自己设置一道心理屏障——算法很难，我肯定很难学会。

现在我可以对有这种想法的朋友很坚决的说一句——咱把问题想复杂了，算法没有我们想象的那么难，相反，它就是编程过程中的一些更加高效的解题方法，说不定咱们在刷题的过程中就已经不知不觉的完成了一些我们认为的比较复杂的算法的编写。

因此我们在学习算法的过程中，我们不应该把算法和编程割裂开来，相反，我们还需要把算法融入到我们平时的编程当中去，这样才能够真正做到在学习算法的同时熟练的掌握算法。

从上述这个角度出发，我才会有狭义算法与广义算法的观点，并且我希望大家在阅读到这里时，都能够以广义算法的观点来看待并学习算法——算法是对特定问题的解决方法的描述。即算法就是编程，编程就是算法，而我们所提到的那些动态规划、贪心……这些算法，则是更加高效的解决问题的方法，也就是一种更优的编程方法。

结语

在今天的内容中我给大家介绍了我自己对算法的一个看法：

• 我们在进行解题、处理实际问题时编写的各种各样的代码就是算法。即算法就是编程，编程就是算法。

对于大家口中的动态规划、贪心、分治……这些算法，我们应该将其视为解决问题时更加高效的方法，也就是更优的编程方法。因此，我们在学习算法的过程中，不应该将算法和编程给割裂开来，它们本就是一体的。

这里要注意，我这里所说的更加高效的方法并不是绝对的，而是相对的。

这里我举一个很简单的例子——我们现在要实现一个将输入的数据直接输出的功能，我们有哪些实现方法呢？

1. 直接通过标准输出的库函数进行输入，如printf、putc、puts、putchar……
2. 通过迭代，将输入的值进行拆分后，按单个字符进行逐位输出
3. 通过递归，将输入的值进行拆分后，按单个字符进行逐位输出

很显然，如果只是将输入的值直接输出的话，我们直接调用库函数的方式会更加的高效，这里如果我们采用迭代或递归的方式来实现的话，就是将这个问题给复杂化了。

再比如，我们如果要在有序数组中查找某个值，平均情况来看，我们通过二分查找的效率显然就要比顺序查找的效率要高，但是如果是在极端情况，就比如要查找的值正好是位于顺序查找的起始点，那么顺序查找的效率就一定要高于二分查找。

这里我们以：[1,2,3,4,5,6,7,8,9,10]为例。在这10个我们如果要从左开始进行顺序查找，那么我们如果要查找的值是1，或者2，那我们采用顺序查找的方式肯定优于二分查找，但是如果我们要查找的值是3~10，那么我们采用二分查找的效率肯定要优于顺序查找的效率。

因此，对于不同的情况，我们应该选用更加合适的解决方法才是一个良好的编程习惯，而大家现在对于一些简单问题的解决方法应该都是没有问题了，我们在这个专栏中要学习的各种算法实际上就是来帮助大家扩充在处理某些复杂问题时的更优的解决方法。

今天的内容到这里就全部结束了，在下一篇内容中我们将介绍《递归》的相关内容，大家记得关注哦！如果大家喜欢博主的内容，可以点赞、收藏加评论支持一下博主，当然也可以将博主的内容转发给你身边需要的朋友。最后感谢各位朋友的支持，咱们下一篇再见！！！