题目描述

今天是小科的生日，小科最好的3个朋友来给他庆祝生日。他们为小科带来了一个大大的正方形蛋糕，确切的说，这个正方形蛋糕由N*N个小方块组成，每个小方块上要么抹了奶油，要么抹了巧克力。小科会将蛋糕沿着小方块的分割线横切一刀，再竖切一刀，刚好切成4块（不会破坏任何一个小方块），出于礼貌，小科会让他的小伙伴们先选择，剩下的一块留给自己，不幸的是小科和他的3个小伙伴都更喜欢奶油，所以小伙伴们都会优先选择奶油更多的蛋糕，而把奶油最少的蛋糕留给小科。小科想知道，如何切才能使他拿到的蛋糕中所包含的奶油小方块尽可能的多。

输入格式

第一行，一个整数N表示正方形蛋糕是由N*N个小方块组成的，2≤N≤100

接下来N行，每行N个整数，分别给出N*N个整数，整数0表示小方块是奶油，整数1表示小方块是巧克力，整数之间用空格隔开

输出格式

一行，一个整数，表示小科拿到的那块蛋糕奶油小方块的最大值

输入输出样例

输入样例1：

3 1 1 1 0 0 1 0 0 1

输出样例1：

1

输入样例2：

4 0 1 0 0 0 0 0 0 0 1 0 0 0 0 1 0

输出样例2：

3

说明

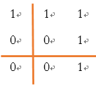
【样例说明1】

如图所示，这样把蛋糕分成4分，小科能够获取的的蛋糕中有是1小方块奶油

【样例说明2】

如图所示，这样把蛋糕分成4份，小科能够获取的的蛋糕中有是3小方块奶油

【耗时限制】1000ms 【内存限制】256MB

这题有难度，本人也是直接嘎掉，关键是二维判断

#include <iostream>
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
LL n,a[110][110],maxn=0;
int main()
{
    cin>>n;
    for(int i=1;i<=n;i++)
        for(int j=1;j<=n;j++) cin>>a[i][j]; 
    
    for(LL i=1;i<=n;i++){
        for(LL j=1;j<=n;j++){
        	LL p1=0,p2=0,p3=0,p4=0,cnt1=1e9;
            for(LL k=1;k<=i;k++)
                for(LL l=1;l<=j;l++) if(!a[k][l]) p4++;
                
            for(LL k=i+1;k<=n;k++)
                for(LL l=1;l<=j;l++) if(!a[k][l]) p3++;
                
            for(LL k=i+1;k<=n;k++)
                for(LL l=j+1;l<=n;l++) if(!a[k][l]) p2++;
                
            for(LL k=1;k<=i;k++)
                for(LL l=j+1;l<=n;l++) if(!a[k][l]) p1++;
                
            cnt1=min(cnt1,min(p1,min(p2,min(p3,p4))));
             maxn=max(maxn,cnt1);
        }
    }
    cout<<maxn;
    return 0;
}