1. 题⽬链接：724.寻找数组的中⼼下标 

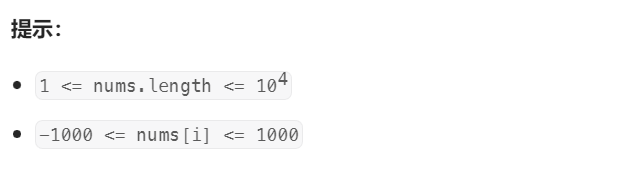
2. 题⽬描述：

3. 解法（前缀和）： 

算法思路：

从中⼼下标的定义可知，除中⼼下标的元素外，该元素左边的「前缀和」等于该元素右边的「后缀 和」。

        ▪ 因此，我们可以先预处理出来两个数组，⼀个表⽰前缀和，另⼀个表⽰后缀和。

        ▪ 然后，我们可以⽤⼀个for 循环枚举可能的中⼼下标，判断每⼀个位置的「前缀和」以及 「后缀和」，如果⼆者相等，就返回当前下标。 

C++算法代码：

class Solution 
{
public:
    int pivotIndex(vector<int>& nums) 
    {
        //左前缀和数组
        vector<int>left(nums.size());
        left[0]=0;
        for(int i=1;i<nums.size();i++)
        {
            left[i]=left[i-1]+nums[i-1];
        }
        //右前缀和数组
        vector<int>right(nums.size());
        right[nums.size()-1]=0;
        for(int i=nums.size()-2;i>=0;i--)
        {
            right[i]=right[i+1]+nums[i+1];
        }
        //判断输出
        for(int i=0;i<nums.size();i++)
        {
            if(left[i]==right[i])
            {
                return i;
            }
        }
        return -1;
    }
};

Java算法代码：

class Solution
{
	public int pivotIndex(int[] nums)
	{
		// lsum[i] 表⽰：[0, i - 1] 区间所有元素的和 
		// rsum[i] 表⽰：[i + 1, n - 1] 区间所有元素的和 
		int n = nums.length;
		int[] lsum = new int[n];
		int[] rsum = new int[n];
		// 预处理前缀和后缀和数组 
		for (int i = 1; i < n; i++)
			lsum[i] = lsum[i - 1] + nums[i - 1];
		for (int i = n - 2; i >= 0; i--)
			rsum[i] = rsum[i + 1] + nums[i + 1];
		// 判断 
		for (int i = 0; i < n; i++)
			if (lsum[i] == rsum[i])
				return i;
		return -1;
	}
}