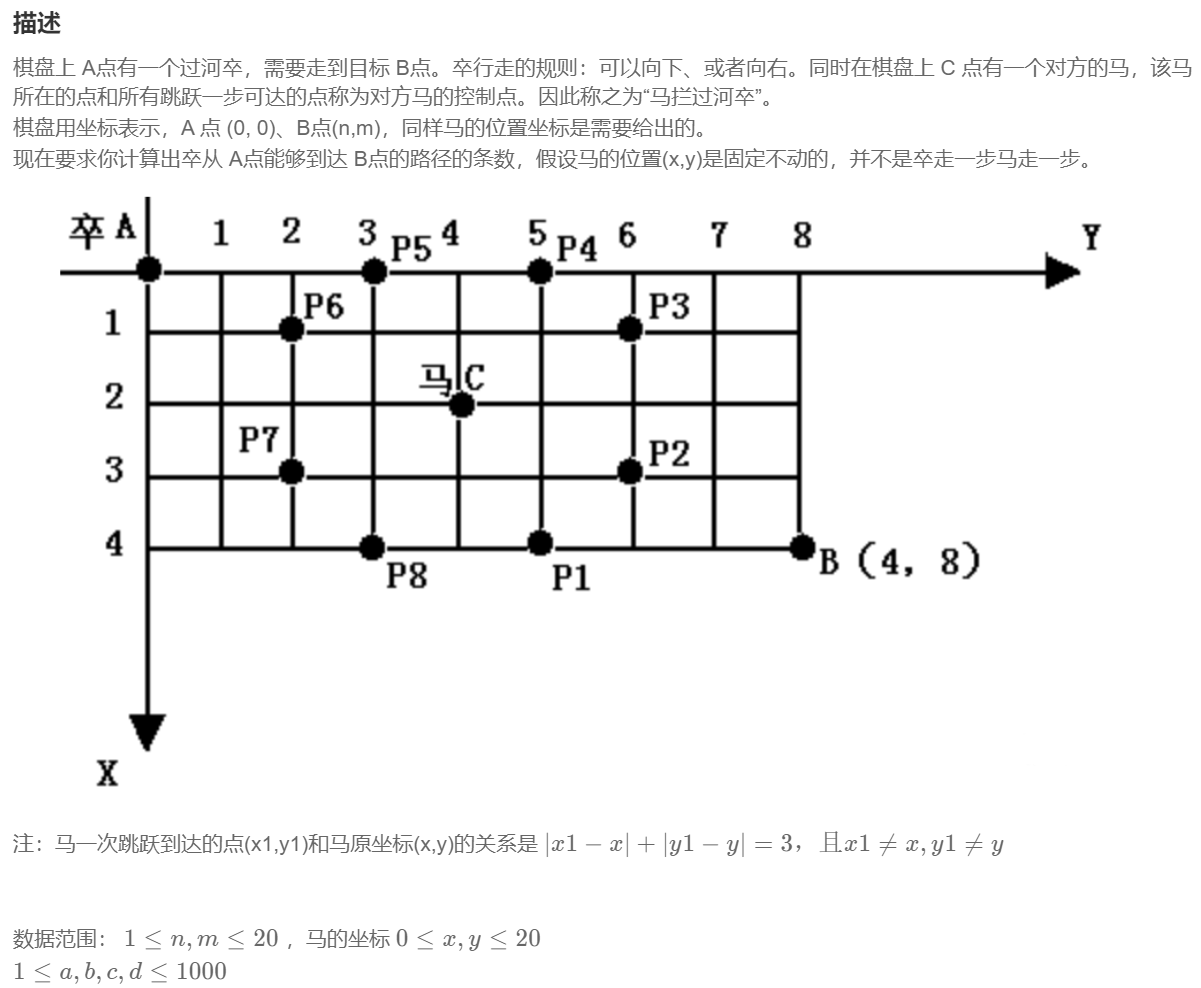
1. 题⽬链接：DP13[NOIP2002普及组]过河卒

2. 题⽬描述：

3. 解法：

算法思路：

简单路径dp问题：

相当于是有障碍物的路径类问题，标记⾛到障碍物上的⽅法数为0即可。

C++算法代码： 

#include <iostream>
#include <vector>
#include <cmath>
using namespace std;
long long dp[25][25];
int main()
{
    //建表
    //n,m为终点坐标，x,y为马的坐标
    int n,m,x,y;
    cin>>n>>m>>x>>y;
    x += 1; y += 1;
    //初始化
    dp[0][1]=1;
    //填表
    for(int i=1;i<=n+1;i++)
    {
        for(int j=1;j<=m+1;j++)
        {
            //走不到的位置给0
            if ((i != x && j != y && abs(i - x) + abs(j - y) == 3) || (i == x && j == y))
            {
                dp[i][j] = 0;
            }
            else
            {
                dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
            }
        }
    }
    //输出
    cout<<dp[n+1][m+1];
    return 0;
}

Java算法代码：

import java.util.Scanner;
// 注意类名必须为 Main, 不要有任何 package xxx 信息 
public class Main
{
	public static void main(String[] args)
	{
		Scanner in = new Scanner(System.in);
		int n = in.nextInt(), m = in.nextInt(), x = in.nextInt(), y =
			in.nextInt();
		long[][] dp = new long[n + 2][m + 2];
		dp[0][1] = 1;
		x += 1; y += 1;
		for (int i = 1; i <= n + 1; i++)
		{
			for (int j = 1; j <= m + 1; j++)
			{
				if (i != x && j != y && Math.abs(i - x) + Math.abs(j - y) == 3
					|| (i == x && j == y))
				{
					dp[i][j] = 0;
				}
				else
				{
					dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
				}
			}
		}
		System.out.println(dp[n + 1][m + 1]);
	}
}