void ShellSort(int* a, int n)
{
int gap = n;
while (gap > 1)
{
// +1保证最后一个gap一定是1
// gap > 1时是预排序
// gap == 1时是插入排序
gap = gap / 3 + 1;
for (size_t i = 0; i < n - gap; ++i)
{
int end = i;
int tmp = a[end + gap];
while (end >= 0)
{
if (tmp < a[end])
{
a[end + gap] = a[end];
end -= gap;
}
else
{
break;
}
}
a[end + gap] = tmp;
}
}
}以上为完成代码实现,以下为详细讲解。
首先,希尔排序有两个过程。
1.预排序:让数组接近有序。
2.插入排序
(默认元素都存在数组a中,一共有a个元素)
预排序,即取一个gap值,gap至今并未直接证明取什么值最好,但大部人都同意gap=gap/3+1(gap初始化为n)效率最高。
为什么gap取值是变化的?因为:
gap越大,大的元素就可以越快跳到后面,小的元素就可以越快跳到前面,但是越不接近有序。gap越小,元素跳的越慢,但是越接近有序。当gap=1的时候就相当于插入排序,数组就有序了。所以我们期望gap取变化的值,那么就可以兼顾他们的优点。即gap取值越来越小可以实现这个想法。
那么gap取值为什么最后+1呢?因为:
gap/3的结果可能为0.1.2,那么最后一次就有可能不能实现插入排序,导致最后排序的数组并不是完全有序的。+1是为了保证最后一次一定是gap=1,那么就一定可以实现插入排序,那么数组就一定有序了。
将所有数据分成gap组,每组内的元素间相隔gap个位置,那么每组就有(n/gap=)3个数据(忽略gap取值中的+1)。然后分别将每一组中的元素进行排序。
接下来我们逐步写代码:
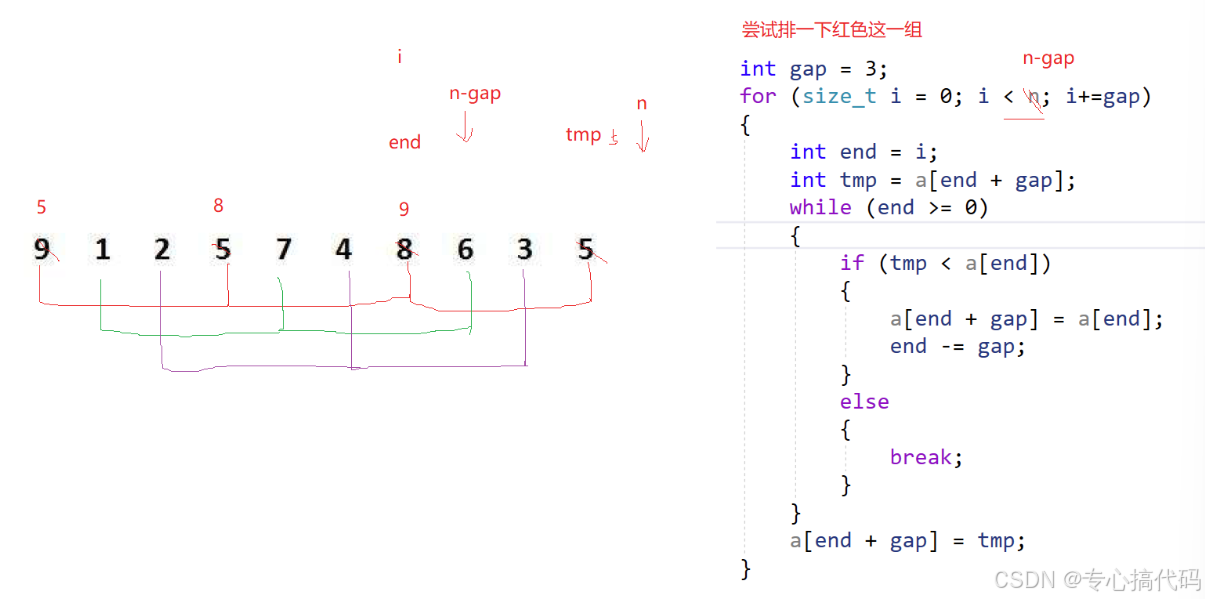
首先排一组:
我们先排红色这一组,我们需要注意的是i的终止位置,同时要注意,我们是用i这个位置的数据与下一个位置的数据来比较大小。数组中最后一个元素的下标为n-1,而且该元素恰好为这一组中的最后一个元素,那么倒数第二个元素的下标为n-1-gap,所以i<n-gap。然后要注意到的是内层while循环的条件,如果下一个位置的数据tmp比end这个位置的数据小,那么我们还要比较tmp是否比end-gap位置的数据小,如果还小,那么end就要一直前移gap个位置,最差的情况是end移动到了0-gap这个位置,就说明此时tmp是它及其它之前的所有元素中最小的那个,那么只需要把end+gap=0这个位置的数据赋值上tmp(0+gap及其之后的元素在while循环中已经被赋值完成了)。
//然后我们想对gap组数据进行排序
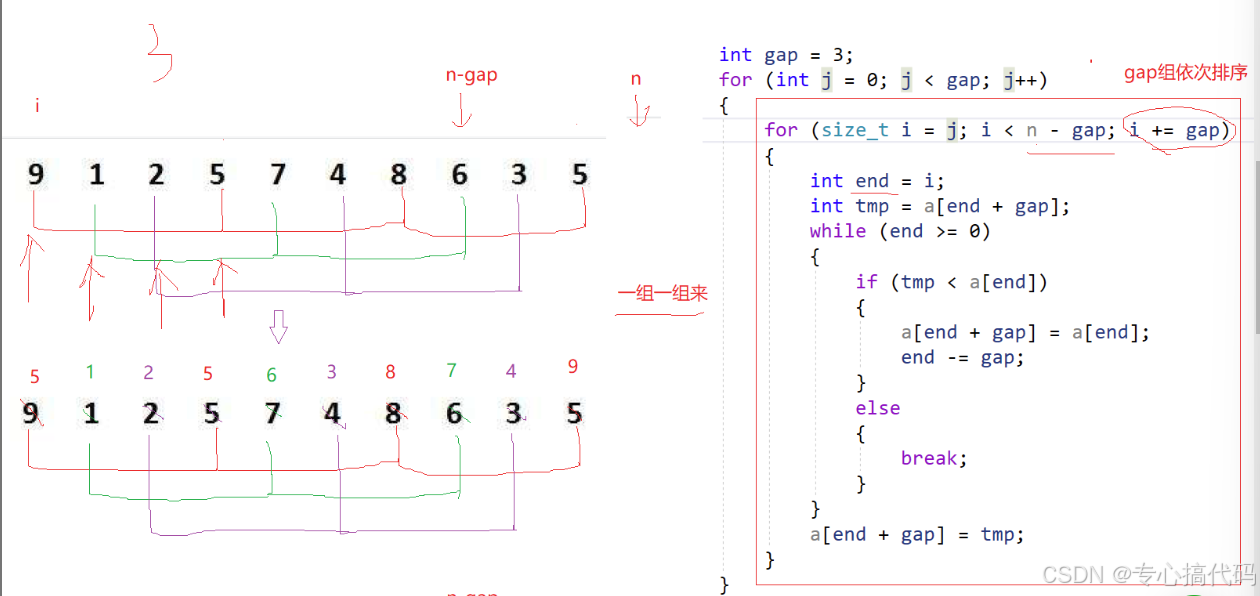
关键点就是end一开始的取值,我们在外面再加一层for循环,来为end赋初值。
//但是我们觉得这样三层循环有点冗余。
这种写法与上一种写法的比较次数是一样的。这种写法是每一组的第一二个元素都比较完了,再比较每一组的第二三个元素,那么最后一组就是n-gap-1与n-1相比,那么就把两层for循环变成了一层for循环。
这一种是多组并着走,上一种是一组一组走。
//最后,我们在最外层再加上while循环,来让gap成为一个不断变化的值。
最后,希尔排序的时间复杂度是O(N^1.3),这是一个大约值,记住就行了,这个特别难算。
//接下来,简单讲一下这个时间复杂度为何难算:
取gap=n/3(忽略+1,影响不大),那么每一趟比较的消耗=每组比较次数*组数。
最坏情况下,第一趟预排序的消耗:(1+2)*(n/3)=n 。将这三个元素看成逆序的,第二个元素交换一次,第三个元素交换两次。gap就是组数。
最坏情况下,第二趟预排序的消耗:(1+2+3+4+5+6+7+8)*(n/9)=4*n 。第二趟gap=n/3/3=n/9,每组9个数据。看成逆序排列,同上一段的讲述。
但是要注意的问题是,每一趟都比前一趟更接近有序,那么就不会是最坏情况下的消耗。
最后一趟已经非常接近有序了,此时gap=1,也就是直接插入排序的消耗:n 。
同时,gap也是变化的值,主导元素一直在变化,导致时间复杂度无法精确的求出来。
那么每一趟的消耗呈现为下面这样的关系:
完结~撒花~