Bootstrap

数据结构--栈

栈的基本概念

1.栈的概念

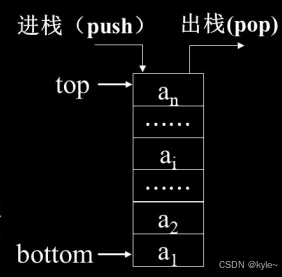
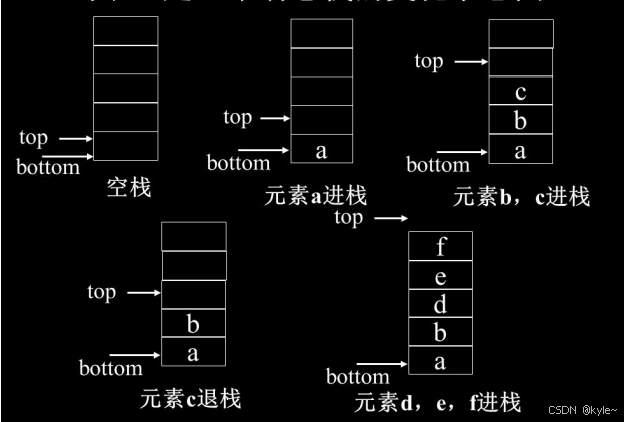
栈(Stack)：是限制在表的一端进行插入和删除操作的线性表。又称为后进先出LIFO (Last In First Out)或先进后出FILO (First In Last Out)线性表。
栈顶(Top)：允许进行插入、删除操作的一端，又称为表尾。用栈顶指针(top)来指示栈顶元素。
栈底(Bottom)：是固定端，又称为表头。
空栈：当表中没有元素时称为空栈。
设栈S=(a1，a2，…an)，则a1称为栈底元素，an为栈顶元素，如图3-1所示。
栈中元素按a1，a2，…an的次序
进栈，退栈的第一个元素应为栈顶元
素。即栈的修改是按后进先出的原则
进行的。
在这里插入图片描述

2.栈的抽象数据类型定义

ADT Stack{
数据对象：D ={ ai
|ai∈ElemSet, i=1,2,…,n，n≥0 }
数据关系：R ={<ai-1
, ai>|ai-1，ai∈D, i=2,3,…,n }
基本操作：初始化、进栈、出栈、取栈顶元素等
} ADT Stack

栈的顺序存储表示

栈的顺序存储结构简称为顺序栈，和线性表相类似，用一维数组来存储栈。根据数组是否可以根据需要增大，又可分为静态顺序栈和动态顺序栈。
◆ 静态顺序栈实现简单，但不能根据需要增大栈的
存储空间；
◆ 动态顺序栈可以根据需要增大栈的存储空间，但实现稍为复杂

栈的动态顺序存储表示

采用动态一维数组来存储栈。所谓动态，指的是栈的大小可以根据需要增加。
◆ 用bottom表示栈底指针，栈底固定不变的；栈顶则随着进栈和退栈操作而变化。用top(称为栈顶指针)指示当前栈顶位置。
◆ 用top=bottom作为栈空的标记，每次top指向栈顶数组中的下一个存储位置。
◆ 结点进栈：首先将数据元素保存到栈顶(top所指的当前位置)，然后然后执行top加1，使top指向栈顶的下一个存储位置;
◆ 结点出栈：首先执行top减1，使top指向栈顶元素的存储位置，然后将栈顶元素取出。
动态堆栈变化示意图
在这里插入图片描述

基本操作

栈的初始化 压栈 弹栈

//栈
#include<stdio.h>
#include<malloc.h>
#define ERROR 0;
#define OK 1;
#define STACK_SIZE 100
#define STACKINCREAMENT 10
typedef int ElemType;

typedef struct sqstack
{
	ElemType *bottom;//栈不存在时值为NULL
	ElemType* top;//栈顶指针
	int stacksize;//当前已分配空间，以元素为单位
}Sqstack;

int Init_Stack(sqstack* S)//初始化，分配空间
{
	S->bottom = (ElemType*)malloc((STACK_SIZE) * sizeof(ElemType));
	if (!S->bottom)return ERROR;
	S->top = S->bottom;//栈空时栈顶和栈底指针相同
	S->stacksize = STACK_SIZE;
	return OK;
}
int push(Sqstack *S, ElemType e)//压栈
{
	if (S->top - S->bottom >= S->stacksize - 1)
	{
		S->bottom = (ElemType*)realloc(S->bottom,(STACKINCREAMENT + STACK_SIZE) * sizeof(ElemType));//栈满追加存储空间
		if (!S->bottom) return ERROR;
		S->top = S->bottom + S->stacksize;
		S->stacksize += STACKINCREAMENT;
	}
	*S->top = e; 
	S->top++;
	return OK;
}
int pop(Sqstack *S, ElemType* e)//弹出栈顶元素
{
	if (S->top == S->bottom)
		return ERROR;
	S->top--;
	*e = *S->top;
	return OK;
}
int main() {
	Sqstack S;//测试
	if(Init_Stack(&S)!= 1){
		printf("Failed to initialise stack\n");
		return OK;
	}
	
	for (int i = 0; i < 15; i++) {
		if (push(&S, i) != 1) {
			printf("failed to push element %d\n", i);
			return 1;
		}
		else {
			printf("push %d onto the stack\n", i);
		}
	}
	ElemType e;
	while (pop(&S, &e) == 1) {
		printf("popped %d form the stack\n", e);
	}
}

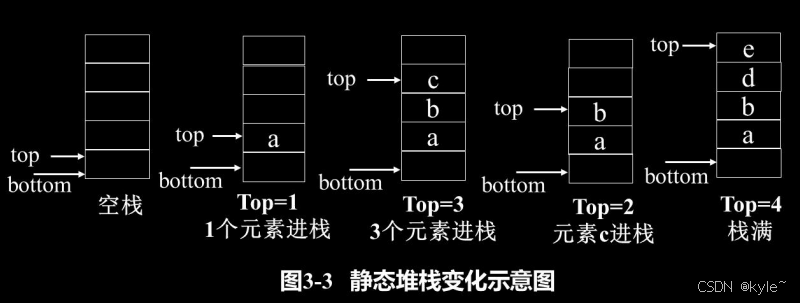
栈的静态顺序存储表示

采用静态一维数组来存储栈

  • 栈底固定不变的，而栈顶则随着进栈和退栈操作变化的，
  • 栈底固定不变的;栈顶则随着进栈和退栈操作而变化，用一个整型变量top(称为栈顶指针)来指示当前栈顶位置。
  • 用top=0表示栈空的初始状态，每次top指向栈顶在数组中的存储位置。
  • 结点进栈:首先执行top加1，使top指向新的栈顶位置，然后将数据元素保存到栈顶(top所指的当前位置)。
  • 结点出栈:首先把top指向的栈顶元素取出，然后执行top减1，使top指向新的栈顶位置。
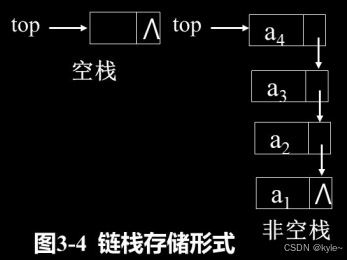
    在这里插入图片描述

链栈

栈的链式存储结构成为链栈，是运算受限的单链表。其插入和删除操作只能在表头位置上进行。因此，链栈没有必要像单链表那样附加头结点，栈顶指针top就是链表的头指针。
在这里插入图片描述

#include <stdio.h>
#include <stdlib.h>

typedef struct Node {//节点
    int data;           
    struct Node* next;  // 指向下一个节点的指针
} Node;

typedef struct Stack {
    Node* top;   // 栈顶指针
} Stack;

void initStack(Stack* s) {
    s->top = NULL;  // 初始化时栈为空
}

int isEmpty(Stack* s) {
    return s->top == NULL;  // 栈顶指针为NULL时栈为空
}

void push(Stack* s, int value) {//入栈操作，top指针在前，下一个入栈元素加载top后，top指针后移，重复即可得到链表
    Node* newNode = (Node*)malloc(sizeof(Node));  // 创建一个新节点
    if (newNode == NULL) {
        printf("Error: Memory allocation failed.\n");
        return;
    }
    newNode->data = value;   // 给新节点赋值
    newNode->next = s->top;   // 新节点的next指针指向当前栈顶
    s->top = newNode;         // 更新栈顶指针为新节点
}

int pop(Stack* s) {// 出栈操作
    if (isEmpty(s)) {
        printf("Error: Stack underflow.\n");
        return -1;  // 返回-1表示栈为空
    }
    Node* temp = s->top;       // 临时保存栈顶元素，包含value和指针
    int value = temp->data;    // 获取栈顶元素的值
    s->top = s->top->next;     // 更新栈顶指针，将栈顶指针向后位移一位
    free(temp);                // 释放栈顶节点的内存
    return value;              // 返回栈顶元素的值
}
int peek(Stack* s) {// 查看栈顶元素
    if (isEmpty(s)) {
        printf("Error: Stack is empty.\n");
        return -1;  // 返回-1表示栈为空
    }
    return s->top->data;  // 返回栈顶元素的值
}

void printStack(Stack* s) {// 打印栈中的元素
    if (isEmpty(s)) {
        printf("Stack is empty.\n");
        return;
    }
    Node* current = s->top;  // 从栈顶开始遍历
    while (current != NULL) {
        printf("%d ", current->data);
        current = current->next;
    }
    printf("\n");
}

void destroyStack(Stack* s) {// 销毁栈
    while (!isEmpty(s)) {
        pop(s);  // 一直出栈直到栈为空
    }
}

int main() {
    Stack s;
    initStack(&s);

    push(&s, 10);
    push(&s, 20);
    push(&s, 30);

    printf("Stack after pushes: ");
    printStack(&s);

    printf("Top element is: %d\n", peek(&s));

    printf("Popped element is: %d\n", pop(&s));

    printf("Stack after pop: ");
    printStack(&s);

    destroyStack(&s);

    return 0;
}

栈的应用

十进制整数N向其它进制数d(二、八、十六）的转换是计算机实现计算的基本问题

//静态顺序栈实现数的进制转换
/*数电二进制转化，短除法，然后写的顺序是从下往上写，正好对应栈的存储结构*/
#include <stdio.h>
#include <stdlib.h>

#define MAX_SIZE 50

// 栈结构体
typedef struct {
    int arr[MAX_SIZE]; //s->arr 是栈的数组存储空间，s->arr[index] 代表栈中的一个元素，index 为该元素的索引位置
    int top;          
} Stack;

// 初始化栈
void initStack(Stack* s) {
    s->top = -1;  // 栈为空，栈顶指针初始化为-1
}

// 判断栈是否为空
int isEmpty(Stack* s) {
    return s->top == -1;
}

// 判断栈是否已满
int isFull(Stack* s) {
    return s->top == MAX_SIZE - 1;
}

// 入栈操作
void push(Stack* s, int value) {
    if (isFull(s)) {
        printf("Stack Overflow!\n");
        return;
    }
    s->arr[++(s->top)] = value;
}

// 出栈操作
int pop(Stack* s) {
    if (isEmpty(s)) {
        printf("Stack Underflow!\n");
        return -1;
    }
    return s->arr[(s->top)--];
}

// 十进制整数转换为指定进制
void convertToBase(int N, int base) {
    Stack s;
    initStack(&s);

    // 边界条件
    if (base < 2 || base > 16) {
        printf("Invalid base! Only bases between 2 and 16 are allowed.\n");
        return;
    }

    // 特殊情况：当N为0时直接输出0
    if (N == 0) {
        printf("0\n");
        return;
    }

    // 进行进制转换
    while (N > 0) {
        int remainder = N % base;
        push(&s, remainder);  // 将余数压入栈
        N = N / base;         // 更新N
    }

    // 输出转换结果
    printf("The result in base %d is: ", base);

    while (!isEmpty(&s)) {
        int value = pop(&s);
        if (value < 10) {
            printf("%d", value);  // 对于0-9直接输出数字
        }
        else {
            printf("%c", value - 10 + 'A');  // 对于10-15输出A-F
        }
    }
    printf("\n");
}

int main() {
    int N, base;

    // 输入十进制数和目标进制
    printf("Enter a decimal number: ");
    scanf("%d", &N);
    printf("Enter the base (2, 8, 16): ");
    scanf("%d", &base);

    // 执行转换
    convertToBase(N, base);

    return 0;
}

在文字处理软件或编译程序设计时，常常需要检查一个字符串或表达式中的括号是否匹配。括号匹配的基本思想是：**从左至右扫描字符串或表达式，每个右括号必须与最近遇到的那个左括号相匹配。**为了实现这一功能，可以利用栈（Stack）这种数据结构来辅助检查。

算法思想：设置一个栈，当读到左括号时，左括号进栈。当读到右括号时，则从栈中弹出一个元素，与读到的左括号进行匹配，若匹配成功，继续读入；否则匹配失败。

栈与递归调用的实现

在程序设计语言中实现递归调用是栈的另一个重要应用。例如树的非递归遍历，就是用栈来模拟的程序的递归执行

  • 递归调用：一个函数直接或间接的调用自己本身，简称递归（Recursive）
  • 递归应该包括两部分：递归规则，终止条件

少年自当扶摇上，揽星衔月逐日光。 —庄子

悦读

道可道，非常道；名可名，非常名。 无名，天地之始，有名，万物之母。 故常无欲，以观其妙，常有欲，以观其徼。 此两者，同出而异名，同谓之玄，玄之又玄，众妙之门。

最新收录
Hive查询函数
jackson反序列化失败InvalidFormatException: Can not deserialize value of type java.util.Date
全国行政区划代码
java基于springboot+vue的旅游信息网站设计与实现
C++课程设计：学生管理系统设计
【服务器篇之linux-yum安装镜像源无效解决】
京东双十一高并发场景下的分布式锁性能优化
Golang中的面向对象继承
新手必备：最佳类 Windows 界面的 Linux 发行版
（附源码）计算机毕业设计SSM流浪猫狗救助站
;