Codeforces Round 940 (Div. 2) and CodeCraft-23(A-D)

题目链接：Dashboard - Codeforces Round 940 (Div. 2) and CodeCraft-23 - Codeforces

A. Stickogon

思路

正多边形意味着要用相等的木棍，相等的木棍最少需要3根才能组成正三角，我们把相等的数的数量除3加起来

代码

void solve(){
    int n;
    cin>>n;
    map<int,int> mp;
    for(int i=1;i<=n;i++){
        int x;cin>>x;
        mp[x]++;
    }
    int cnt=0;
    for(auto &[x,y]:mp){
        if(y>=3) cnt+=y/3;
    }
    cout<<cnt<<"\n";
}

B. A BIT of a Construction

思路

构造，要满足第二个条件，我们可以将其中的一个数为x=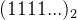 $(1111...)_{2}$ ，x<=k，这样就可以保证最多1

这样在第二个条件下满足第一个条件，再构造一个数y=k-x，其余数全为0

再特判一下n=1时即可

代码

#include<bits/stdc++.h>
using namespace std;

#define vcoistnt ios_base::sync_with_stdio(false); cin.tie(NULL); cout.tie(NULL); 
#define int long long
#define ull unsigned long long
#define bit __builtin_popcount
#define lowbit(x) ((x)&-(x))
#define vi vector<int>
#define vb vector<bool>
typedef pair<int,int> pll;

const int N=2e5+10;
const int inf=1e18;
const int mod=998244353;

void solve(){
    int n,k;
    cin>>n>>k;
    int x=0,ct=0;
    while(x<=k){
        x+=(1ll<<ct);
        ct++;
    }
    x-=(1ll<<(ct-1));
    if(n==1){
        cout<<k<<"\n";return;
    }
    cout<<x<<" "<<k-x<<" ";
    for(int i=3;i<=n;i++){
        cout<<"0 ";
    }
    cout<<"\n";
}
signed main() {
    vcoistnt
    int _=1;
    cin>>_;
    while(_--) solve();
    return 0;
}

C. How Does the Rook Move?

思路

在想这题的时候我们发现将已经确定的点所在的行和列删掉，剩下的仍然可以拼接成一个小的(n-x)*(n-x)的棋盘，如果该点在对角线上x=1,否则x=2

那么问题就转换为了一个x*x的棋盘有多少种不同的配置，那么我们很容易就能够想到dp，从1*1开始递推，可以发现当n>=3时，dp[i]=dp[i-1]+2*(i-1)*dp[i-2]

dp[i-1]:选择新添加的对角线上的那个元素

2*(i-1)*dp[i-2]:选择行或列上除对角线元素的某个元素

当然也可以从x*x -> 1*1上用记忆化搜索来实现，只是思想不同

代码

//1.逆向来用dp实现-------------------------------------<
const int N=3e5+10;
const int inf=1e18;
const int mod=1e9+7;


vi dp(N);
void init(){
    dp[0]=1;dp[1]=1;dp[2]=3;
    for(int i=3;i<N;i++){
        dp[i]=dp[i-1]+2*(i-1)*dp[i-2];
        dp[i]%=mod;
    }
}


void solve(){
    int n,k;
    cin>>n>>k;
    
    for(int i=1;i<=k;i++){
        int x,y;
        cin>>x>>y;
        if(x!=y) n-=2;
        else n--;
    }
    
    cout<<dp[n]<<"\n";
}
signed main() {
    vcoistnt
    init();
    int _=1;
    cin>>_;
    while(_--) solve();
    return 0;
}
//2.正向来，用记忆化搜索来实现---------------------------<
const int N=3e5+10;
const int inf=1e18;
const int mod=1e9+7;

vector<int> dp(N,-1);

int dfs(int x){
    if(dp[x]!=-1) return dp[x];
    int sum=0;
    sum=(sum+(x+x-2)*dfs(x-2))%mod;
    sum=(sum+dfs(x-1))%mod;
    return dp[x]=sum%mod;
}

void solve(){
    int n,k;
    cin>>n>>k;
    for(int i=1;i<=k;i++){
        int x,y;
        cin>>x>>y;
        if(x!=y) n-=2;
        else n--;
    }
    cout<<dfs(n)%mod<<"\n";
}
signed main() {
    vcoistnt
    int _=1;
    dp[0]=1;
    dp[1]=1;
    dp[2]=3;
    cin>>_;
    while(_--) solve();
    return 0;
}

D. A BIT of an Inequality

思路

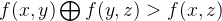
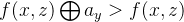
根据异或的性质，我们可以将 $f(x,y)\bigoplus f(y,z)>f(x,z)$ 转化成 $f(x,z)\bigoplus a_{y}>f(x,z)$ 或 $f(x,y-1)\bigoplus f(y+1,z)>f(x,z)$

那么接下来我们的任务就是枚举一下a[i]看其满足条件的包含a[i]的子数组的数量即可，

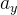
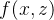
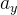
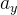
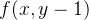
思考一下 $a_{y}$ 什么情况下能使 f(x,z) 相对于没有异或前变小，可以发现我们只需要看 $a_{y}$ 的二进制下最高位为1的那个即可，因为其他位数的异或之后的贡献是一定要小于最高位的，设 $a_{y}$ 最高位1是第i位，那么例如当 f(x,y-1) 的第i位是1且 $f(y+1,z)$ 的第i位是0时，这样异或上 $a_{y}$ 其值便会减少

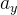
那么答案就是【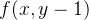 f(x,y-1) 的第i位是1的子数组的数量 * $f(y+1,z)$ 的第i位是0】+

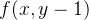
【 f(x,y-1) 的第i位是0的子数组的数量 * $f(y+1,z)$ 的第i位是1】

我们设 pref[i][j][0/1] 表示前缀，从前 j 位a 里包含j的子数组异或和第i位为0/1的数量，根据异或性质状态转移便是

1.a[j]第i位为0时， $pref[i][j][0]=1+pre[i][j-1][0]$ （多了一个以a[j]单独为一个子数组）

pre[i][j][1]=pre[i][j-1][1]

2.a[j]第i位为1时， $pref[i][j][1]=1+pref[i][j-1][0]$

pref[i][j][0]=pre[i][j-1][1]

同理设 suff[i][j][0/1]

那么最终答案： $ans+=pref[z][i-1][1]*(1+suff[z][i+1][0]);$

$ans+=(1+pref[z][i-1][0])*suff[z][i+1][1];$

z为a[i]的最高位为1的位置，可以用__builtin_clz()实现

代码

#include<bits/stdc++.h>
using namespace std;

#define vcoistnt ios_base::sync_with_stdio(false); cin.tie(NULL); cout.tie(NULL); 
#define int long long
#define ull unsigned long long
#define bit __builtin_popcount
#define lowbit(x) ((x)&-(x))
#define vi vector<int>
#define vb vector<bool>
typedef pair<int,int> pll;

const int N=1e5+10;
const int inf=1e18;
const int mod=998244353;

int pref[30][N][2];
int suff[30][N][2];
//pref[i][j][0/1] 表示前j个数中，包含j的子数组异或和第i位为0/1的子数组的数量
//suff[i][j][0/1] 表示后j个数中，包含j的子数组异或和第i位为0/1的子数组的数量

void solve(){
	int n;cin>>n;
	vi a(n+1);
	for(int i=1;i<=n;i++) cin>>a[i];
	
	for(int i=0;i<30;i++) suff[i][n+1][0]=suff[i][n+1][1]=0;

	for(int i=0;i<30;i++){
		for(int j=1;j<=n;j++){
			int t=(a[j]&(1<<i));
			if(t==0){
				pref[i][j][0]=1+pref[i][j-1][0];
				pref[i][j][1]=pref[i][j-1][1];
			}else{
				pref[i][j][0]=pref[i][j-1][1]; 
				pref[i][j][1]=1+pref[i][j-1][0];
			}
		}
		for(int j=n;j>=1;j--){
			int t=(a[j]&(1<<i));
			if(t==0){
				suff[i][j][0]=1+suff[i][j+1][0];
				suff[i][j][1]=suff[i][j+1][1];
			}else{
				suff[i][j][0]=suff[i][j+1][1];
				suff[i][j][1]=1+suff[i][j+1][0];
			}
		}
	}

	int ans=0;
	for(int i=1;i<=n;i++){
		int z=31-__builtin_clz(a[i]);
		ans+=pref[z][i-1][1]*(1+suff[z][i+1][0]);
		ans+=(1+pref[z][i-1][0])*suff[z][i+1][1];
	}
	cout<<ans<<"\n";

}
signed main() {
	vcoistnt
	int _=1;
	cin>>_;
	while(_--) solve();
	return 0;
}