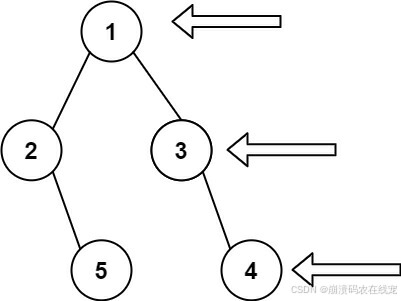
给定一个二叉树的 根节点 root，想象自己站在它的右侧，按照从顶部到底部的顺序，返回从右侧所能看到的节点值。

示例 1:

输入: [1,2,3,null,5,null,4]
输出: [1,3,4]

示例 2:

输入: [1,null,3]
输出: [1,3]

示例 3:

输入: []
输出: []

提示:

• 二叉树的节点个数的范围是 [0,100]
• -100 <= Node.val <= 100 

解法一：队列（

执行用时分布

0ms击败100.00%

） 

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<int> rightSideView(TreeNode* root) {
        vector<int> ans;
        if(root==nullptr)
        return {};
        queue<TreeNode*> q;
        q.push(root);
        while(!q.empty()){
            int size=q.size();
            for(int i=0;i<size;i++){
                TreeNode* node=q.front();
                q.pop();

                if(i==size-1)
                ans.push_back(node->val);

                if(node->left)
                q.push(node->left);
                if(node->right)
                q.push(node->right);
            }
        }
        return ans;
    }
};

这段代码是使用BFS（广度优先搜索）的方法来解决二叉树的右视图问题。

首先，定义一个空的vector ans 作为结果集。

然后，创建一个队列q，并将根节点root压入队列中。

接下来，进行一个while循环，直到队列为空。在每一次循环中，首先获取当前队列的大小size，这是为了只取出当前层级的节点。

然后，使用一个for循环，从队列中取出size个节点。在循环中，首先获取当前节点node，然后将其弹出队列。

接着，判断是否为当前层级的最后一个节点，如果是，则将该节点的值node->val加入到结果集ans中。

然后，判断当前节点是否有左子节点和右子节点，如果有，则将其分别压入队列中。

最后，返回结果集ans。

这个算法的思路是按层遍历二叉树，并将每一层最右边的节点的值加入到结果中。由于是按层遍历，所以对于每一层最右边的节点，它们一定是在每层最后加入到队列中的节点。因此，只需要在每层遍历开始前判断当前节点是否为该层最后一个节点，如果是，则将其值加入到结果中。

解法二：深度优先遍历，哈希表、栈 

class Solution {
public:
    // 定义一个函数来获取二叉树的右视图
    vector<int> rightSideView(TreeNode* root) {
        // 使用一个unordered_map来存储每个深度上最右边的节点的值
        unordered_map<int, int> rightmostValueAtDepth;

        // 初始化最大深度为-1
        int max_depth = -1;

        // 定义两个栈：一个用于存储节点，一个用于存储深度
        stack<TreeNode*> nodeStack;
        stack<int> depthStack;
        nodeStack.push(root);
        depthStack.push(0);

        // 当节点栈不为空时，进行遍历
        while (!nodeStack.empty()) {
            TreeNode* node = nodeStack.top(); nodeStack.pop();
            int depth = depthStack.top(); depthStack.pop();

            // 如果节点不为空
            if (node != NULL) {
                // 更新二叉树的最大深度
                max_depth = max(max_depth, depth);

                // 如果当前深度没有对应的节点，插入当前节点的值
                if (rightmostValueAtDepth.find(depth) == rightmostValueAtDepth.end()) {
                    rightmostValueAtDepth[depth] = node -> val;
                }

                // 将左子节点和其深度压入栈
                nodeStack.push(node -> left);
                nodeStack.push(node -> right);
                depthStack.push(depth + 1);
                depthStack.push(depth + 1);
            }
        }

        // 创建一个vector来存储结果
        vector<int> rightView;
        // 遍历每个深度，并将对应的节点值添加到结果vector中
        for (int depth = 0; depth <= max_depth; ++depth) {
            rightView.push_back(rightmostValueAtDepth[depth]);
        }

        // 返回结果vector
        return rightView;
    }
};

首先，定义一个unordered_map来存储每个深度上最右边的节点的值。初始化最大深度为-1。

然后，定义两个栈，一个用于存储节点(nodeStack)，一个用于存储深度(depthStack)。将根节点root压入节点栈和深度栈中，并将深度设置为0。

接下来，进行一个while循环，直到节点栈为空。在每一次循环中，首先获取节点栈的顶部节点node和深度栈的顶部深度depth，并将其弹出栈。

然后，判断当前节点是否为空。如果不为空，则更新二叉树的最大深度max_depth为当前深度depth和max_depth的较大值。

接着，判断当前深度是否在unordered_map中存在对应的节点值。如果不存在，则将当前节点的值node->val插入unordered_map中对应的深度depth。

最后，将当前节点的左子节点和右子节点以及对应的深度分别压入节点栈和深度栈中。这样，在下一次循环中，就可以从栈中取出下一层级的节点。

在while循环结束后，创建一个vector rightView来存储结果。

然后，使用一个for循环，从深度0到最大深度遍历，将unordered_map中对应深度的节点值添加到rightView中。

最后，返回结果vector rightView。

这个算法的思路是通过遍历二叉树并记录每个深度上最右边的节点的值，然后将这些值按照深度的顺序存储在结果vector中，即为二叉树的右视图。