- 实验名称
实验四 数组和函数
- 实验目的
(1)掌握一维、二维数组以及字符数组的定义、元素引用和编程方法。
(2)掌握字符串常用程序的设计方法。
(3)掌握函数定义和调用的方法,以及函数参数传递的方式。
(4)理解变量的作用域及生存期。
- 实验题目
- 编写程序计算Fibonacci数列的前40项。(要求每行输出4个数)
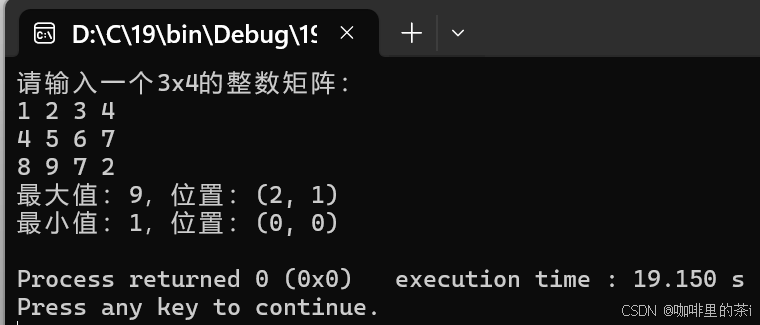
- 从键盘上输入一个3×4
的整数矩阵,找出其中最大值和最小值,记录它们的行号和列号并输出。
- 编写程序将2个字符串连接起来(不使用strcat函数)并输出。
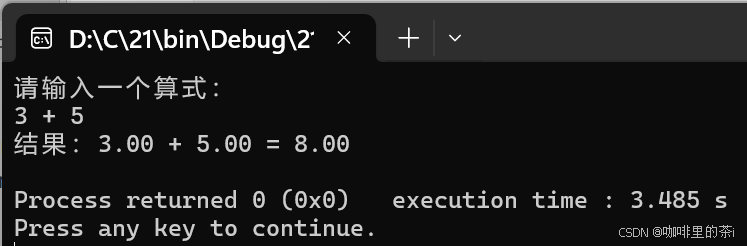
- 编程实现一个具有+,-
,×,÷,%
运算功能的简单计算器。(通过函数实现)
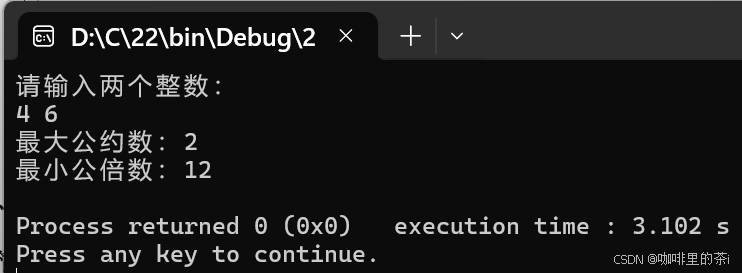
- 任意输入2个整数,编写2个函数分别求这2个整数的最大公约数和最小公倍数,结果在主函数中输出。
- 实验环境
硬件:个人电脑;软件:Visual C++ 6.0
- 实验代码及结果(程序运行结果请以截屏图给出)
- 源程序代码:
| #include <stdio.h> int main() { int fibonacci[40]; fibonacci[0] = 0; fibonacci[1] = 1; for (int i = 2; i < 40; i++) fibonacci[i] = fibonacci[i - 1] + fibonacci[i - 2]; for (int i = 0; i < 40; i++) { printf("%d ", fibonacci[i]); if ((i + 1) % 4 == 0) // 使用 (i + 1) % 4 来判断是否是每行的最后一个数字 printf("\n"); } return 0; } |
运行结果为:
- 源程序代码:
| #include <stdio.h> #include <limits.h> int main() { int matrix[3][4]; int max_value = INT_MIN, min_value = INT_MAX; int max_row, max_col, min_row, min_col; printf("请输入一个3x4的整数矩阵:\n"); for (int i = 0; i < 3; i++) { for (int j = 0; j < 4; j++) { scanf("%d", &matrix[i][j]); // 更新最大值和最小值及其位置 if (matrix[i][j] > max_value) { max_value = matrix[i][j]; max_row = i; max_col = j; } if (matrix[i][j] < min_value) { min_value = matrix[i][j]; min_row = i; min_col = j; } } } printf("最大值:%d,位置:(%d, %d)\n", max_value, max_row, max_col); printf("最小值:%d,位置:(%d, %d)\n", min_value, min_row, min_col); return 0; } |
运行结果为:
- 源程序代码:
| #include <stdio.h> int main() { char str1[100] = "Hello, "; char str2[] = "World!"; int i = 0, j = 0; // 找到str1的末尾 while (str1[i] != '\0') i++; // 将str2的字符逐个复制到str1的末尾 while (str2[j] != '\0') { str1[i] = str2[j]; i++; j++; } // 在str1的末尾添加字符串结束符'\0' str1[i] = '\0'; // 输出连接后的字符串 printf("%s\n", str1); return 0; } |
运行结果为:
- 源程序代码:
| #include <stdio.h> double add(double a, double b) { return a + b; } double subtract(double a, double b) { return a - b; } double multiply(double a, double b) { return a * b; } double divide(double a, double b) { return a / b; } int modulus(int a, int b) { return a % b; } // 主函数 int main() { char operator; double num1, num2; double result; printf("请输入一个算式:\n"); scanf("%lf %c %lf", &num1, &operator, &num2); // 根据运算符执行相应的运算 switch (operator) { case '+': result = add(num1, num2); break; case '-': result = subtract(num1, num2); break; case '*': result = multiply(num1, num2); break; case '/': result = divide(num1, num2); break; case '%': // 执行取模运算 result = modulus(num1, num2); break; default: printf("错误:无效的运算符。\n"); return 1; // 返回非零值表示程序异常终止 } // 输出其他运算的结果 printf("结果:%.2lf %c %.2lf = %.2lf\n", num1, operator, num2, result); return 0; } |
运行结果为:
- 源程序代码:
| #include <stdio.h> // 求最大公约数的递归函数(辗转相除法) int gcd(int a, int b) { if (b == 0) return a; else return gcd(b, a % b); } // 求最小公倍数的函数(利用GCD) int lcm(int a, int b, int gcd_result) { return (a * b) / gcd_result; } // 主函数 int main() { int num1, num2; int gcd_result, lcm_result; // 输入两个整数 printf("请输入两个整数:\n"); scanf("%d %d", &num1, &num2); // 计算最大公约数(使用递归辗转相除法) gcd_result = gcd(num1, num2); // 计算最小公倍数 lcm_result = lcm(num1, num2, gcd_result); printf("最大公约数:%d\n", gcd_result); printf("最小公倍数:%d\n", lcm_result); return 0; } |
运行结果为:
六、实验心得(请对每个实验题目编程及调试运行中遇到的问题及解决方案进行简单总结)