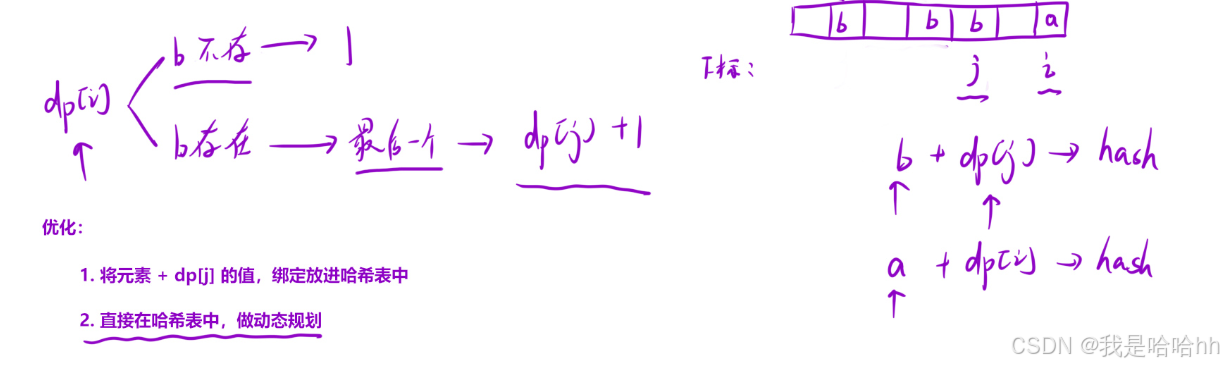目录
子序列系列问题(数组中不连续的一段)
经过上一个专题子数组的学习后,我对动态规划思想越来越深刻,有了更加深入的理解,明白了要完成一个动态规划题目,是要对所有当前位置的dp[i]进行分类讨论,分析清楚里面所有的种类情况才能动手写代码,最重要的就是分清楚细节问题,了解每一种情况下的初始化,要让初始化状态不影响后面的填表顺序,最后就是根据dp状态表达式来确定返回值~
接下来就要进入更难、更重要的专题,子序列系列问题,是动态规划更为常见的一种思想:
1. 最⻓递增⼦序列(medium)
解析:
1.状态表达式:
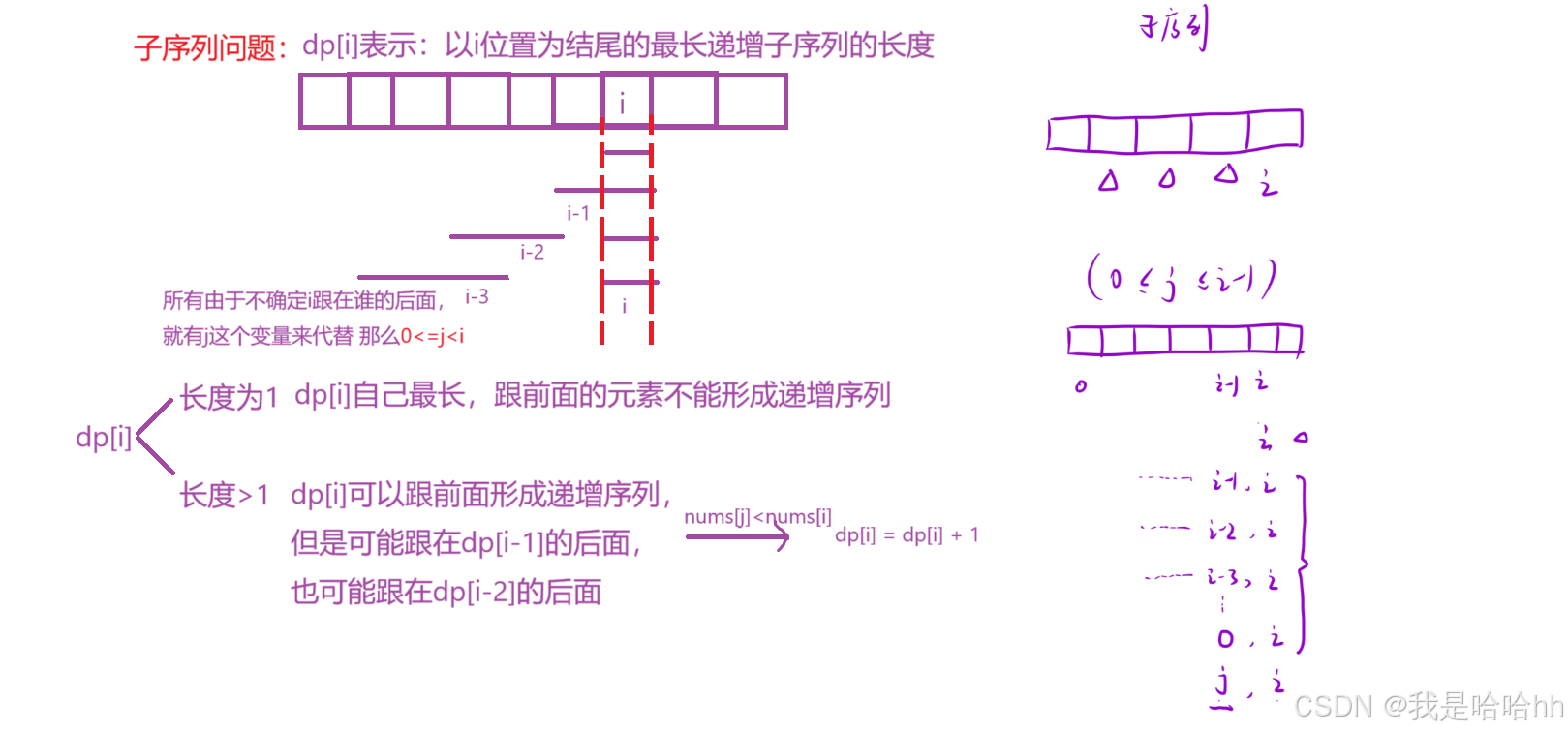
dp[i]表示:以i位置为结尾的最长递增子序列的长度
2.状态转移方程
在满足nums[j] < nums[i] 的条件下:dp[i]=max(dp[j]+1,dp[i]);
3.初始化:
因为题目要求是最长的长度,所以就算当前元素不满足跟前面的递增关系,所以最短也是为长度1,这一题初始化不需要添加新的虚拟节点所以开空间只要开n个即可
4.填报顺序:
从左往右
5.返回值:
返回dp最大的递增长度即可
代码编写:
class Solution {
public:
int lengthOfLIS(vector<int>& nums) {
int n=nums.size();
vector<int> dp(n,1);
int ret=1;
for(int i=0;i<n;i++)
{
for(int j=0;j<i;j++)
{
if(nums[i]>nums[j]) dp[i]=max(dp[j]+1,dp[i]);
ret=max(ret,dp[i]);
}
}
return ret;
}
};总结:
这是一道很经典的子序列模板题,一定要落实在落实!在分析当前位置应该跟在前面nums的哪一位时,这时就考虑到了j的取值范围,j--> [0,i-1] 那么就可以保证不会错过当前值跟在前面所有nums[j]的每一种情况,然后取最大值
2. 摆动序列(medium)
题目意思很简单,就是在整个数组里面找出最长的摆动子序列
解析:
1.状态表达式:
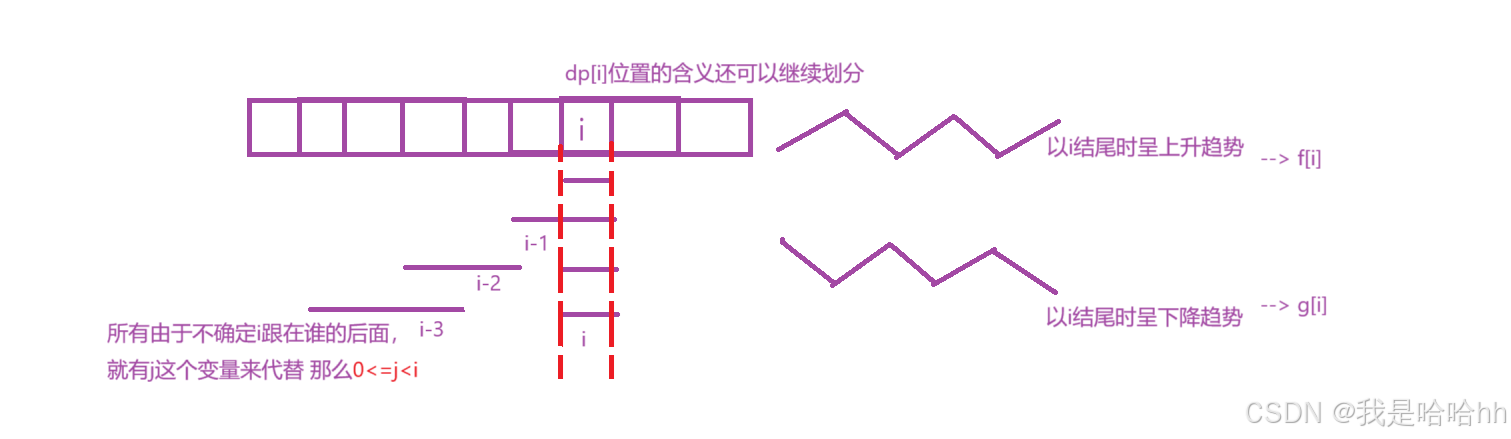
假如这一题跟之前一样:dp[i]表示:以i位置为结尾的所有子序列中最长的摆动子序列
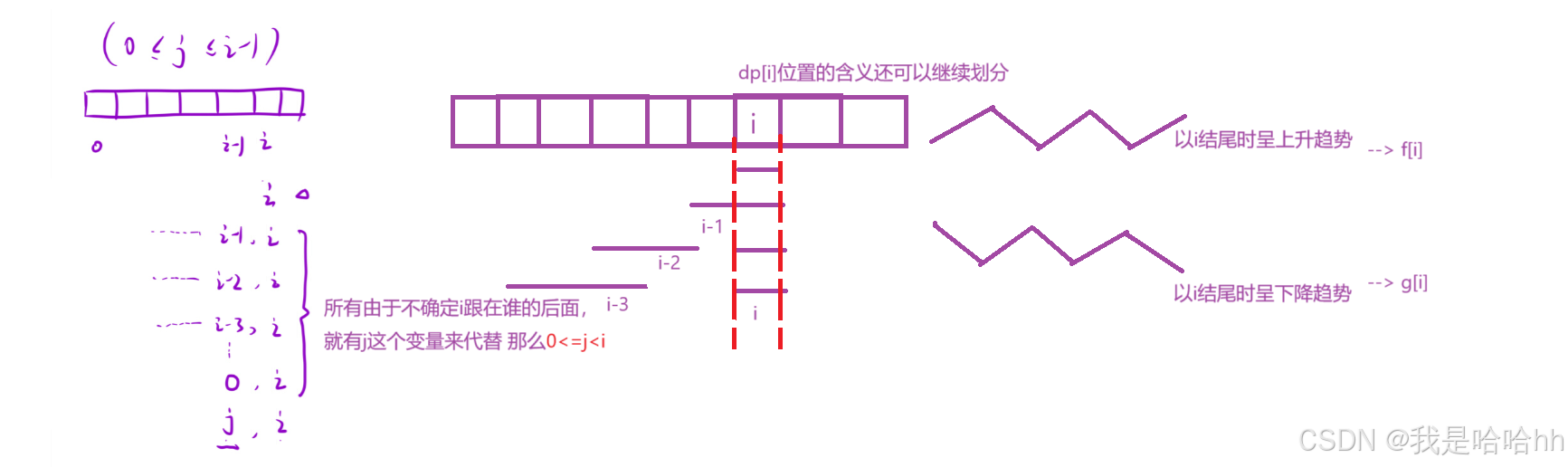
所以dp[i]位置继续划分成当前位置为结尾的时候呈上升趋势还是下降趋势,分别设置:
f[i]表示:以i位置为结尾的所有子序列里面呈上升趋势的最长摆动序列
g[i]表示:以i位置为结尾的所有子序列里面呈下降趋势的最长摆动序列
2.状态转移方程:
判断条件:
呈上升趋势:if(nums[i]>nums[j]) --> f[i]=max(f[i],g[j]+1);
呈下降趋势:if(nums[i]<nums[j]) --> g[i]=max(g[i],f[j]+1);
由于子序列内存在多种可能,来判断当前元素应该跟在前面哪一个元素的后面,所以要用j来定义前面所有元素的可能
3.初始化:
这一题仍然是长度问题,所以每一个为位置都能单独成为一个长度1,不用开虚拟空间
4.填表顺序:
从左往右填
5.返回值:
通过状态表达式可以知道,返回f[i] 和 g[i] 的最大值即可
代码编写:
class Solution {
public:
int wiggleMaxLength(vector<int>& nums) {
int n=nums.size();
int ret=1;
vector<int> f(n,1);
auto g=f;
for(int i=1;i<n;i++)
{
for(int j=0;j<i;j++)
{
if(nums[i]>nums[j])
{
f[i]=max(f[i],g[j]+1);
}
else if(nums[i]<nums[j])
{
g[i]=max(g[i],f[j]+1);
}
ret=max(f[i],max(ret,g[i]));
}
}
return ret;
}
};总结:
这是一道很经典的多状态子序列问题,要将当前位置的dp进行每一个状态的表达,然后在进行下一步分析
3. 最⻓递增⼦序列的个数(medium)
题目意思很简单,就是求出最长子序列的个数
解析:
在写这一题之前先说一个小demo(小贪心)
在数组中找出最大值出现的次数:
我们可以分别设计一个maxval来记录最大值和count计数器来记录最大值出现的次数,怎么样是不是很简单
1.状态表达式:
跟以前一样dp[i]表示:以i位置为结尾的所有子序列中,最长递增子序列的个数
但是这样只定义出了求出最长递增子序列的个数,完全是不够的,因为我们还需要求出最长的递增子序列的长度,才能进行计算个数
所以这里我们设置两个dp表分别来计数:
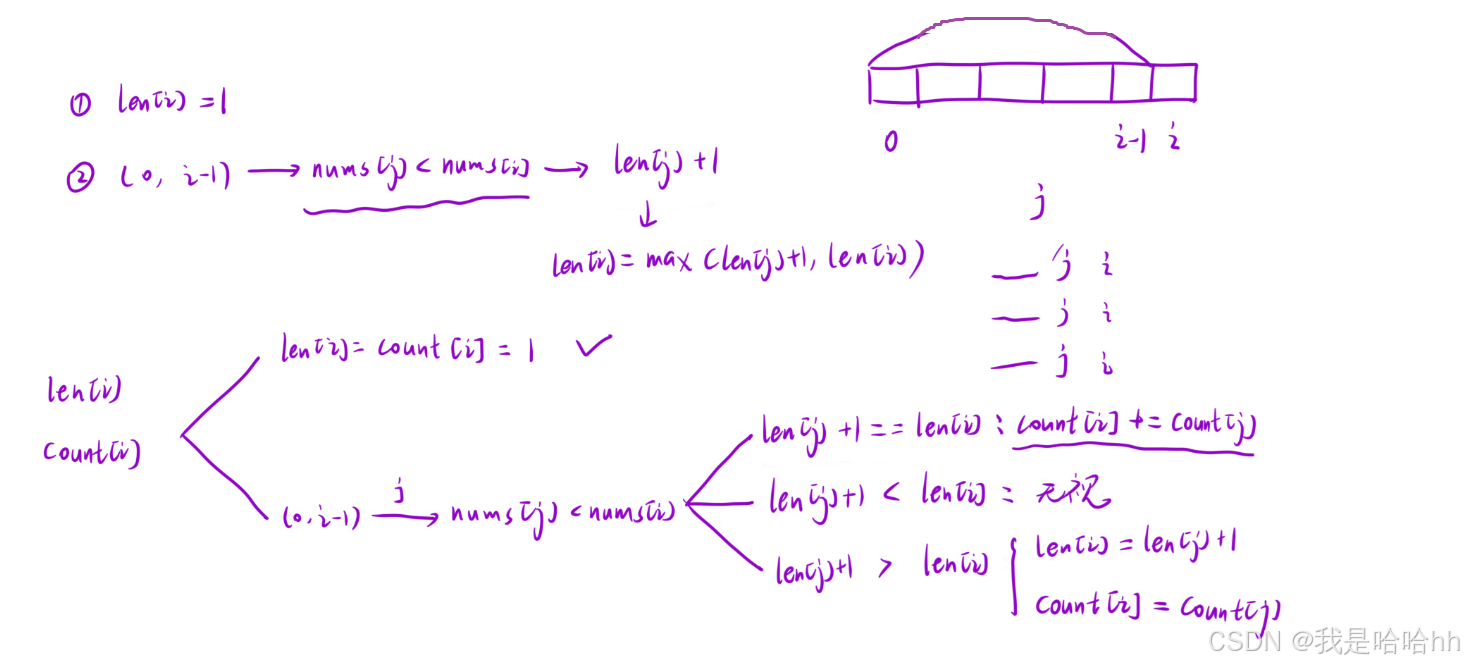
len[i]表示:以i位置元素为结尾的所有子序列中,最长递增子序列的“长度”
count[i]表示:以i位置元素为结尾的所有子序列中,最长递增子序列的“个数”
2.状态转移方程:
判断条件:
必须发生在nums[j] < nums[i] 的条件下,才能满足递增子序列,从而求出最长的递增子序列:
然后对两个dp表进行从头开始遍历,使用那个小demo,遇到比当前位置要长的子序列,就跟新len[i] = len[j] +1 同时更新count[i] = count[j] 注意这里并不是从1开始计算,而是当前长度变成是在count[j]的条件下变长的,所以count[j] 满足的条件下,现在也同时满足。
当前的len[i] == len[j]+1的时候,说明当前位置的nums[i]跟在nums[j]时同时满足已经存在的最长递增子序列,直接让count[i]进行计数即可 count[i] += count[j]
if(len[j]+1==len[i])
{
count[i]+=count[j];
}
else if(len[j]+1>len[i])
{
len[i]=len[j]+1;
count[i]=count[j];
}3.初始化:
将所有的dp表都初始化为1 , 因为不论是长度还是出现的次数,最小都是1
4.填表顺序:
从左往右进行遍历
5.返回值:
返回值是一个小细节:
我们有两种办法:
1.求出最长的递增子序列后,才重新遍历一遍然后专门求最长递增子序列出现的次数
2.继续用那个小demo,设置
int retlen=1;int retcount=1;
然后再一次遍历中直接求解,用retlen 来与len[i]进行比较,如果retlen==len[i] 就让retcount+=count[i]进行计数;
如果retlen[i] < len[i] 说明存在了更大的递增子序列,retlen=len[i]; retcount=count[i];就重新更新retlen 和 retcount
编写代码:
class Solution {
public:
int findNumberOfLIS(vector<int>& nums) {
int n=nums.size();
vector<int> len(n,1);
vector<int> count(n,1);
int retlen=1,retcount=1;
for(int i=1;i<n;i++)
{
for(int j=0;j<i;j++)
{
if(nums[i]>nums[j])
{
if(len[j]+1==len[i])
{
count[i]+=count[j];
}
else if(len[j]+1>len[i])
{
len[i]=len[j]+1;
count[i]=count[j];
}
}
}
if(retlen == len[i]) retcount+=count[i];
else if(retlen < len[i]) retlen=len[i],retcount=count[i];
}
return retcount;
}
};总结:
这一题也是一道非常好的模板题,一定要下去多总结,多思考,为什么会设置两个dp表呢,为什么可以一次遍历用小demo来既记录最长长度 又更新最长长度出现的次数
4. 最⻓数对链(medium)
解析:
1.状态表达式:
dp[i]表示:以i位置为结尾的最长数对的长度
2.状态转移方程:
判断条件:
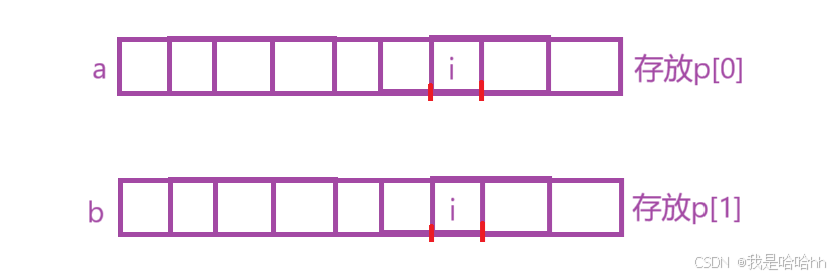
p[i][0] > p[i-1][1] 的时候可以满足dp[i]=max(dp[i],dp[j]+1);
所以将p排序后专门存放到a数组和b数组中即可
3.初始化:
因为这题也是求长度,所以初始化dp全为1即可
4.填表顺序:
从左往右
5.返回值:
返回dp的最长长度即可
代码编写:
class Solution {
public:
int findLongestChain(vector<vector<int>>& pairs) {
int n=pairs.size();
sort(pairs.begin(),pairs.end(),[&](const vector<int>& a,const vector<int>& b)
{
return a[0]<b[0];
});
vector<int> a(n);
auto b = a;
for(int i=0;i<n;i++)
{
a[i]=pairs[i][0];
b[i]=pairs[i][1];
}
vector<int> dp(n,1);
int ret=1;
for(int i=1;i<n;i++)
{
for(int j=0;j<i;j++)
{
if(a[i]>b[j])
{
dp[i]=max(dp[i],dp[j]+1);
}
ret=max(ret,dp[i]);
}
}
return ret;
}
};总结:
这是一道很有意义的题目,适合自己主动分析后,一步步得出结论,还是很有成就感的
5. 最⻓定差⼦序列(medium)
求出数组中最长的定差子序列的长度
解析:
1.状态表达式:
dp[i]表示:以i位置为结尾的最长的定差子序列的最长长度
2.状态转移方程:
判断条件:当满足定差序列:arr[i]==arr[j]+difference
if(arr[i]==arr[j]+difference) dp[i]=max(dp[i],dp[j]+1);3.初始化:
仍然是求长度,所以初始化为1
4.填表顺序:
从右往左
5.返回值:
返回dp表内最大的一个值
代码编写:
class Solution {
public:
int longestSubsequence(vector<int>& arr, int difference) {
int n=arr.size();
int ret=1;
vector<int> dp(n,1);
for(int i=1;i<n;i++)
{
for(int j=0;j<i;j++)
{
if(arr[i]==arr[j]+difference) dp[i]=max(dp[i],dp[j]+1);
ret=max(ret,dp[i]);
}
}
return ret;
}
};但其实上面写的那么简略就是因为跟前面几题的做法步骤一模一样,但是这题数据范围太大,接近O(N^2)了,会超时,所以我们要进行优化;
优化:
题目意思:a - b =diff
那么b = a - diff
所以状态转移方程:
将元素和dp[] 值直接放入hash表内,都不需要dp表,直接再hash表内做动态规划,只需要再O(1)的时间下找到对应的值
用hash表来充当dp表,只做一次遍历,不用回头做第二次遍历,用hash表来存储<int,int>两个int对应的值:arr[i] - dp[i]
hash[arr[i]] = hash[arr[i]-difference] + 1;该状态转移方程意思就是当前位置的dp值(a)= b位置的dp值 + 1
也就是说最前的一个b每次都会被后面的b给覆盖,不用担心找不到离a最近的b
如果当前b不存在,也就是单独自己是一个序列,也不用担心被存到hash表内,因为最终都会是0 + 1 =1
当b存在的时候,就只考虑离a最近的一个b,才可能会出现更长的子序列
代码编写:
class Solution {
public:
int longestSubsequence(vector<int>& arr, int difference) {
int n=arr.size();
int ret=1;
unordered_map<int,int> hash; //arr[i] - dp[i]
hash[arr[0]]=1;
for(int i=1;i<n;i++)
{
hash[arr[i]] = hash[arr[i]-difference] + 1;
ret=max(ret,hash[arr[i]]);
}
return ret;
}
};总结:
这一题的优化思路跟上面几题不同,这一题的优化实在hash表内做dp,又是一个很值得学习的方法
6. 最⻓的斐波那契⼦序列的⻓度(medium)
求最长的斐波那契子序列的长度
解析:
1.状态表达式:
按部就班:
dp[i]表示:以i位置为结尾的最长斐波那契子序列的长度
如果按照这样来写,那么就只能保证以i位置为结尾的数字来判断,而斐波那契数至少需要两个序列结尾数才能判断当前序列是否为斐波那契序列,所以我们要多加一维
因为只要我们能够得出当前序列的最后两个数,当前序列就被定死了,所以我们可以单独考虑当前序列的长度
dp[i][j]表示:以i位置和j位置为结尾的最长的斐波那契子序列的长度(i<j)
2.状态转移方程:
判断当前位置是否存在i位置之前的那一个数字:a = arr[j] - arr[i]
如果存在,就说明可以满足斐波那契序列的要求,然后在判断当前位置:
dp[i][j] =max(dp[k][i] + 1,dp[i][j]);
class Solution {
public:
int lenLongestFibSubseq(vector<int>& arr) {
int n=arr.size();
vector<vector<int>> dp(n,vector<int>(n,2));
int ret=0;
for(int j=2;j<n;j++)
{
for(int i=1;i<j;i++)
{
for(int k=0;k<i;k++)
{
if(arr[j]==arr[k]+arr[i]) dp[i][j]=max(dp[k][i]+1,dp[i][j]);
ret=max(dp[i][j],ret);
}
}
}
return ret==2?0:ret;
}
};可以看出当前位置的三层循环绝对会超时,快逼近O(n^3)
所以对于寻找a这个数,我们可以利用hash表直接映射值与下标的关系来进行寻找:
unordered_map<int,int> hash; //arr[i] - i 值与下标对应
for(int i=0;i<n;i++) hash[arr[i]] = i;
这样每次判断a是否存在只用再O(1)内就能判断出来:
int a=arr[j] - arr[i];
if(hash.count(a)&&hash[a]<i) dp[i][j]=max(dp[hash[a]][i]+1,dp[i][j]);
此时可以看出当a再hash表内存在时,前当前下标小于i,就可以得到dp[i][j] = dp[hash[a]][i] + 1的状态转移方程
3.初始化:
由于填表时,我们设置的是i=1,j=2开始填表,为了满足后续填表的正确,我们默认a,b,c是满足斐波那契序列的状态,所以初始化dp表时全部都初始化为2,表示最短的序列也是从2开始,一旦有满足的条件,就进行dp+1
4.填表顺序:
从左往右,从上往下
5.返回值:
返回dp表内最大值
代码编写:
class Solution {
public:
int lenLongestFibSubseq(vector<int>& arr) {
int n=arr.size();
vector<vector<int>> dp(n,vector<int>(n,2));
int ret=0;
unordered_map<int,int> hash; //arr[i] - i 值与下标对应
for(int i=0;i<n;i++) hash[arr[i]] = i;
for(int j=2;j<n;j++)
{
for(int i=1;i<j;i++)
{
int a=arr[j] - arr[i];
if(hash.count(a)&&hash[a]<i) dp[i][j]=max(dp[hash[a]][i]+1,dp[i][j]);
ret=max(dp[i][j],ret);
}
}
return ret==2?0:ret;
}
};总结:
这一题是一道很好的二维模板题,要完全考虑清楚必须再两个状态下进行求解,考虑完美出当前位置要满足斐波那契序列的条件是在二维的状态下,能够完美的求出当前序列的样子,因为只要我们能够得出当前序列的最后两个数,当前序列就被定死了,所以我们可以单独考虑当前序列的长度
7. 最⻓等差数列(medium)
解析:
1.状态表达式:
依旧是按部就班:
dp[i]表示:以i位置为结尾的最长等差数列的子序列的长度
dp[i][j] 表⽰:以 i 位置以及 j 位置的元素为结尾的所有的⼦序列中,最⻓的等差序列的⻓度。规定⼀下 i < j 。
2.状态转移方程:
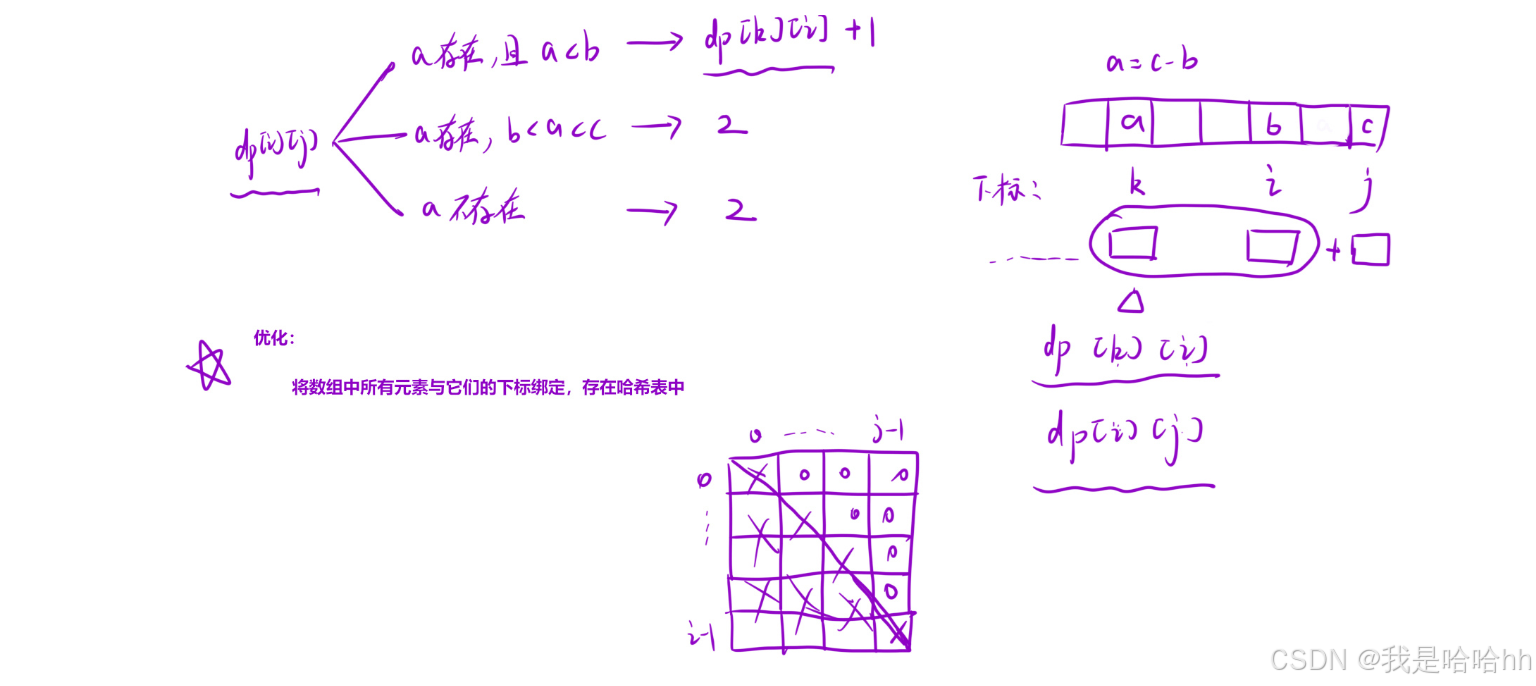
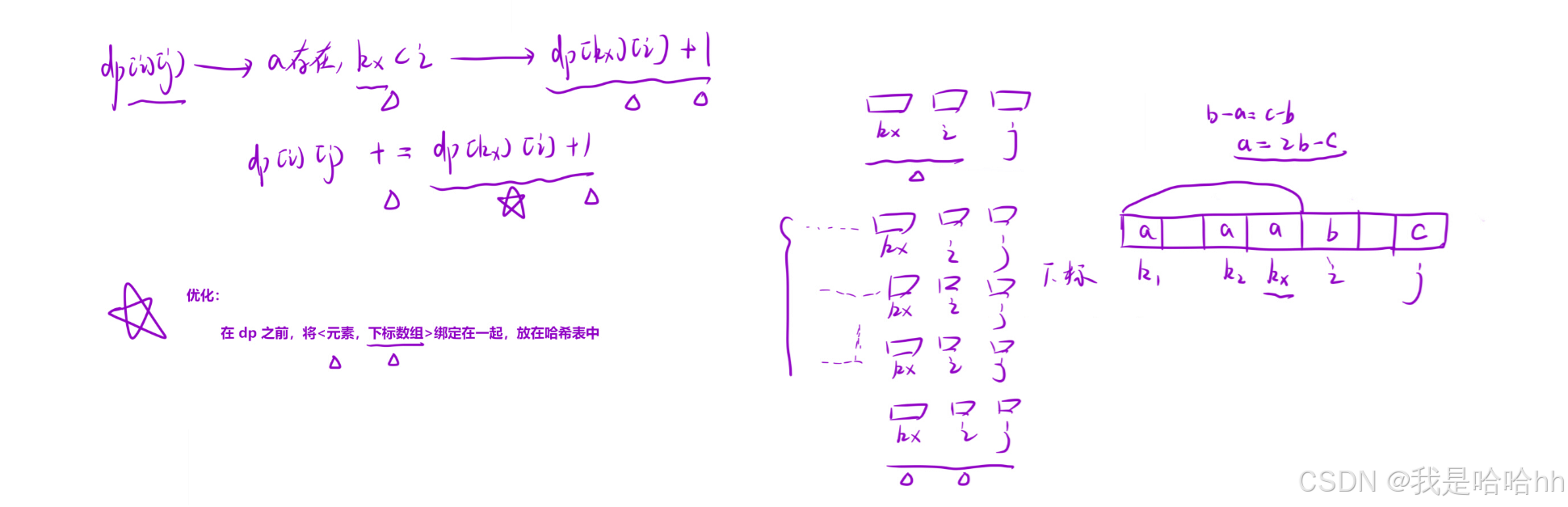
设 nums[i] = b, nums[j] = c ,那么这个序列的前⼀个元素就是 a = 2 * b - c 。我们根据 a 的情况讨论:
a. a 存在,下标为 k ,并且 a < b :此时我们需要以 k 位置以及 i 位置元素为结尾的最⻓等差序列的⻓度,然后再加上 j 位置的元素即可。于是 dp[i][j] = dp[k][i] + 1 。这⾥因为会有许多个 k ,我们仅需离 i 最近的 k 即可。因此任何最⻓的都可以以 k为结尾;b. a 存在,但是 b < a < c :此时只能两个元素⾃⼰玩了, dp[i][j] = 2 ;c. a 不存在:此时依旧只能两个元素⾃⼰玩了, dp[i][j] = 2 。
优化点:我们发现,在状态转移⽅程中,我们需要确定 a 元素的下标。因此我们可以将所有的元素 + 下标绑定在⼀起,放到哈希表中,这⾥有两种策略:
a. 在 dp 之前,放⼊哈希表中。这是可以的,但是需要将下标形成⼀个数组放进哈希表中。这样时间复杂度较⾼,我帮⼤家试过了,超时。b. ⼀边 dp ,⼀边保存。这种⽅式,我们仅需保存最近的元素的下标,不⽤保存下标数组。但是 ⽤这种⽅法的话,我们在遍历顺序那⾥,先固定倒数第⼆个数,再遍历倒数第⼀个数。这样就

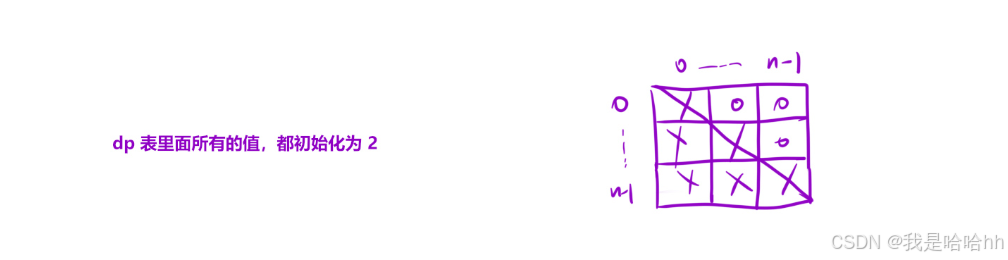
a. 先固定倒数第⼆个数;b. 然后枚举倒数第⼀个数。
代码编写:
class Solution {
public:
int longestArithSeqLength(vector<int>& nums) {
int n=nums.size();
vector<vector<int>> dp(n,vector<int>(n,2));
unordered_map<int,int> hash;
hash[nums[0]]=0;
int ret=2;
for(int i=1;i<n-1;i++)
{
for(int j=i+1;j<n;j++)
{
int diff=nums[j]-nums[i];
int a=nums[i]-diff;
if(hash.count(a)&&hash[a]<i) dp[i][j]=max(dp[hash[a]][i]+1,dp[i][j]);
ret=max(ret,dp[i][j]);
}
hash[nums[i]]=i;
}
return ret;
}
};总结:
这一题的遍历顺序不一样,因为要求出最长的等差数列子序列,我们就不能在开头就奖所有的nums与下标进行对应,因为这样会影响后面求等差序列的子序列长度,我们必须要遍历完一个倒数第二个数nums[i] 就添加一个nums[i] 在hash表内,因为这样下标会被进行覆盖成离nums[j]最近的一个值,所以要遍历一个,添加一个。
这一题应该好好的跟上一题进行总结对比,这样能够更有收获
8. 等差数列划分II - ⼦序列(hard)
求出数组中所拥有的等差子序列的个数
解析:
1.状态表达式:
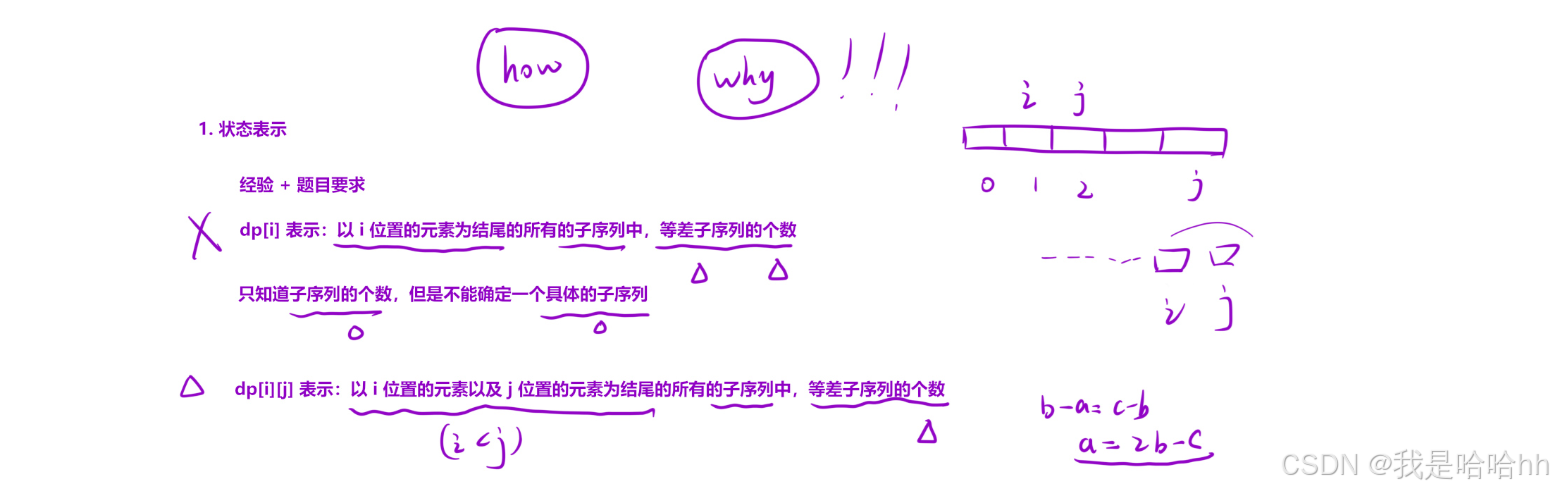
按部就班:dp[i]表示:以i位置为结尾的等差子序列的个数
如果按照这样来确定状态表达式,那么都不能确定一个等差子序列,因为一个等差子序列是至少要有两个元素才能确定一个完整的等差子序列,它要包含公差
所以要按照一个子序列结尾的两个元素来进行确定:
dp[i][j]表示:以i位置的元素和j位置的元素为结尾的所有子序列中,等差子序列的个数(i<j)
2.状态表达式:
由于当前最后结尾的两个元素来确定一个等差子序列,就说a这个元素就已经被确定下来了:
a = nums[i]*2-nums[j]
所以我们只需要知道整个数组内每一个a元素的下标即可:
由于当前位置的最后两个元素是跟在a元素后面的,所以因为a元素和nums[i] 元素组成的等差子序列的个数 也就是等于nums[j]元素等差子序列的个数,那么dp[i][j] += dp[kx][i],唯一不同的就是多了一个a , nums[i], numsp[j]这三个元素组成的一个子序列:
dp[i][j] += dp[kx][i] + 1
3.初始化:
dp表在最坏的情况下,就只有两个元素能够确定,不能成为一个等差子序列,所以个数是0,dp表初始化为0即可
4.填表顺序:
从左往右
5.返回值:
返回dp表内的所有可能情况的和
代码编写:
class Solution {
public:
int numberOfArithmeticSlices(vector<int>& nums) {
int n=nums.size();
unordered_map<long long,vector<long long>> hash;
vector<vector<int>> dp(n,vector<int>(n));
for(int i=0;i<n;i++)
hash[nums[i]].push_back(i);
int ret=0;
for(int j=2;j<n;j++)
{
for(int i=1;i<j;i++)
{
long long a=(long long)nums[i]-nums[j]+nums[i];
if(hash.count(a))
{
for(auto e : hash[a])
{
if(e<i)
{
dp[i][j]+=dp[e][i]+1;
}
}
}
ret+=dp[i][j];
}
}
return ret;
}
};总结:
这一个题目细节很多,真的要好好总结一下,跟前面几题的差别在哪,不能碰到一个题目就想着这题为什么不会写,应该怎么写,而是要想清楚,这一题为什么要这么写!多想想why?