【数据结构与算法 | 图篇】Dijkstra算法（单源最短路径算法）

1. 前言

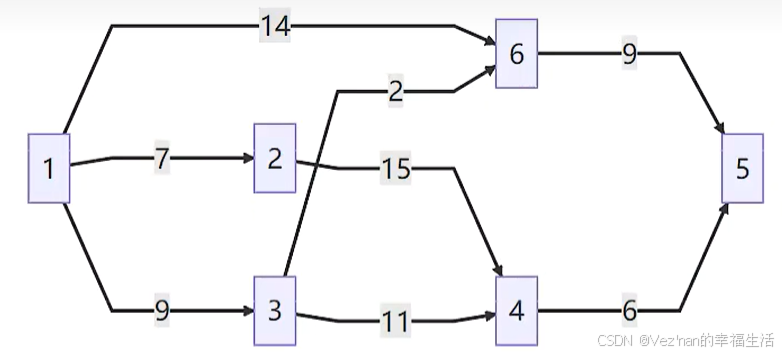
由图：

如果我们想要求得节点1到节点5（也可以是其他节点）的最短路径，我们可以使用Dijkstra算法。

2. 步骤与思路

1. 将所有顶点标记为未访问(顶点类的visited属性设置为false)。创建一个未访问顶点的集合。

2. 为每个顶点分配一个临时距离值：

对于我们的初始顶点，将其设置为0；
对于所有其他顶点，将其设置为无穷大。

3. 每次选择最小临时距离的未访问节点作为当前顶点。

4. 对于当前顶点，遍历其所有未访问的邻居，并更新它们的临时距离为更小。

例如，1->6的距离是14，而1->3->6的距离是11。这时将距离更新为11.
否则，将保留上次距离值。

5. 当前顶点的邻居处理完后，把它从未访问集合中删除。

3. 顶点类与边类

public class Vertex {
    // 顶点的名字，用来区分顶点
    String name;
    // 与该顶点有关的边的集合
    List<Edge> edges;
    // 判断是否已经被遍历
    boolean visited = false;
    // 初始距离为无穷大
    int dist = INF;
    // INF表示无穷大
    final static int INF = Integer.MAX_VALUE;
    // 该顶点在最短路径中的前一个顶点
    Vertex prev = null;
    public Vertex(String name) {
        this.name = name;
    }

    public String getName() {
        return name;
    }
}


public class Edge {
    // 表示边上被箭头指向的顶点
    Vertex linked;
    // 权重
    int weight;

    public Edge(Vertex linked) {
        this.linked = linked;
        weight = 1;
    }

    public Edge(Vertex linked, int weight) {
        this.linked = linked;
        this.weight = weight;
    }
}

4. 总代码：

public class Dijkstra {
    public static void main(String[] args) {
        List<Vertex> list = new ArrayList<>();
        // 建立顶点联系
        Vertex v1 = new Vertex("1");
        Vertex v2 = new Vertex("2");
        Vertex v3 = new Vertex("3");
        Vertex v4 = new Vertex("4");
        Vertex v5 = new Vertex("5");
        Vertex v6 = new Vertex("6");

        v1.edges = new ArrayList<>();
        v1.edges.add(new Edge(v3, 9));
        v1.edges.add(new Edge(v2, 7));
        v1.edges.add(new Edge(v6, 14));

        v2.edges = new ArrayList<>();
        v2.edges.add(new Edge(v4, 15));

        v3.edges = new ArrayList<>();
        v3.edges.add(new Edge(v6, 2));
        v3.edges.add(new Edge(v4, 11));

        v4.edges = new ArrayList<>();
        v4.edges.add(new Edge(v5, 6));

        v5.edges = new ArrayList<>();

        v6.edges = new ArrayList<>();
        v6.edges.add(new Edge(v5, 9));

        // 第1步：
        list.add(v1);
        list.add(v2);
        list.add(v3);
        list.add(v4);
        list.add(v5);
        list.add(v6);
        // v1作为初始顶点
        dijkstra(list, v1);

    }
    public static void dijkstra(List<Vertex> list, Vertex v) {
        List<Vertex> graph = new ArrayList<>(list);
        // 将初始顶点v的dist值设置为0
        v.dist = 0;
        while (!graph.isEmpty()){
            // 第3步：每次选择最小的临时距离的未访问节点作为当前节点
            Vertex i = ChooseMinDistVertex(graph);
            UpdateNeighboursDist(i);
            graph.remove(i);
            // 表示已经被处理完了
            i.visited = true;
        }
//        for (Vertex i : list){
//            System.out.println("v" + i.name + "   " + i.dist);
//        }
        // 打印最短路径中，一个顶点的前一个顶点是谁
        for(Vertex i : list){
            System.out.println("v" + i.name + (i.prev != null ? i.prev : null));
        }
    }
    private static Vertex ChooseMinDistVertex(List<Vertex> list){
        int min = 0;
        int dist = list.get(min).dist;
        for(int i = 0; i < list.size(); i++) {
            if(dist > list.get(i).dist){
                min = i;
                dist = list.get(i).dist;
            }
        }
        return list.get(min);
    }
    private static void UpdateNeighboursDist(Vertex v) {
        // 对于当前顶点，遍历其所有未访问的顶点
        for(Edge e : v.edges){
            if(!e.linked.visited){
                if(v.dist + e.weight < e.linked.dist){
                    e.linked.dist = v.dist + e.weight;
                    e.linked.prev = v;
                }
            }
        }
    }
}

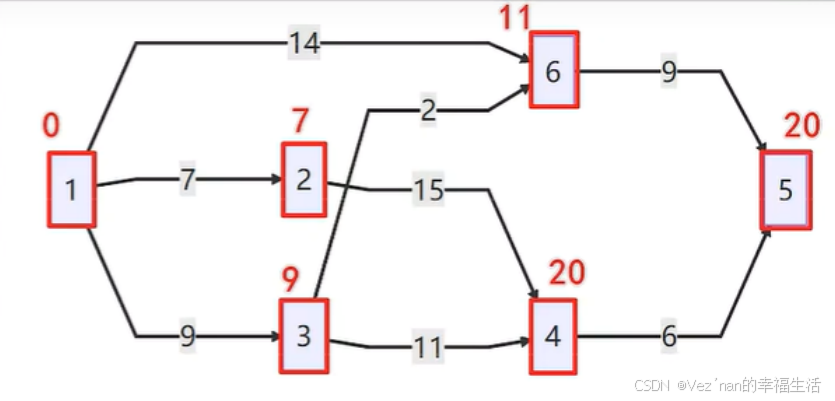
如图：

输出为：

5. 改进的Dijkstra算法