蓝桥杯备考：二叉树详解

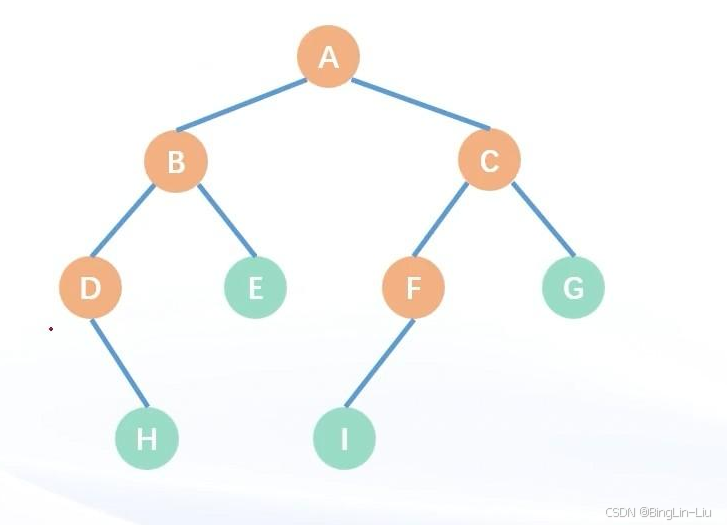
二叉树的概念和相关术语

二叉树的定义：每个结点度至多为2的树，叫二叉树

二叉树的子树有左右之分不可以随意颠倒顺序，也就是说二叉树是有序树

二叉树=根结点+左子树+右子树

满二叉树：就是把每一层的结点都铺满

满二叉树的性质：1° 结点个数为 2的h次方-1

2°深度为 h = log（n+1)

3° 如果满二叉树按照层序遍历的顺序来编号的话，从根结点开始从1开始编号，那么i结点的左孩子是i*2，右孩子是i*2+1，父亲结点就是i/2

完全二叉树就是从右往前依次删除一些结点

二叉树的存储

顺序存储

顺序存储结构就是用数组存储

在完全二叉树那里，我们学到了，如果按照层序遍历编号的话，我们把结点按照下标依次存在数组里面，我们只需要用满二叉树的性质来找结点的左孩子右孩子和父亲即可

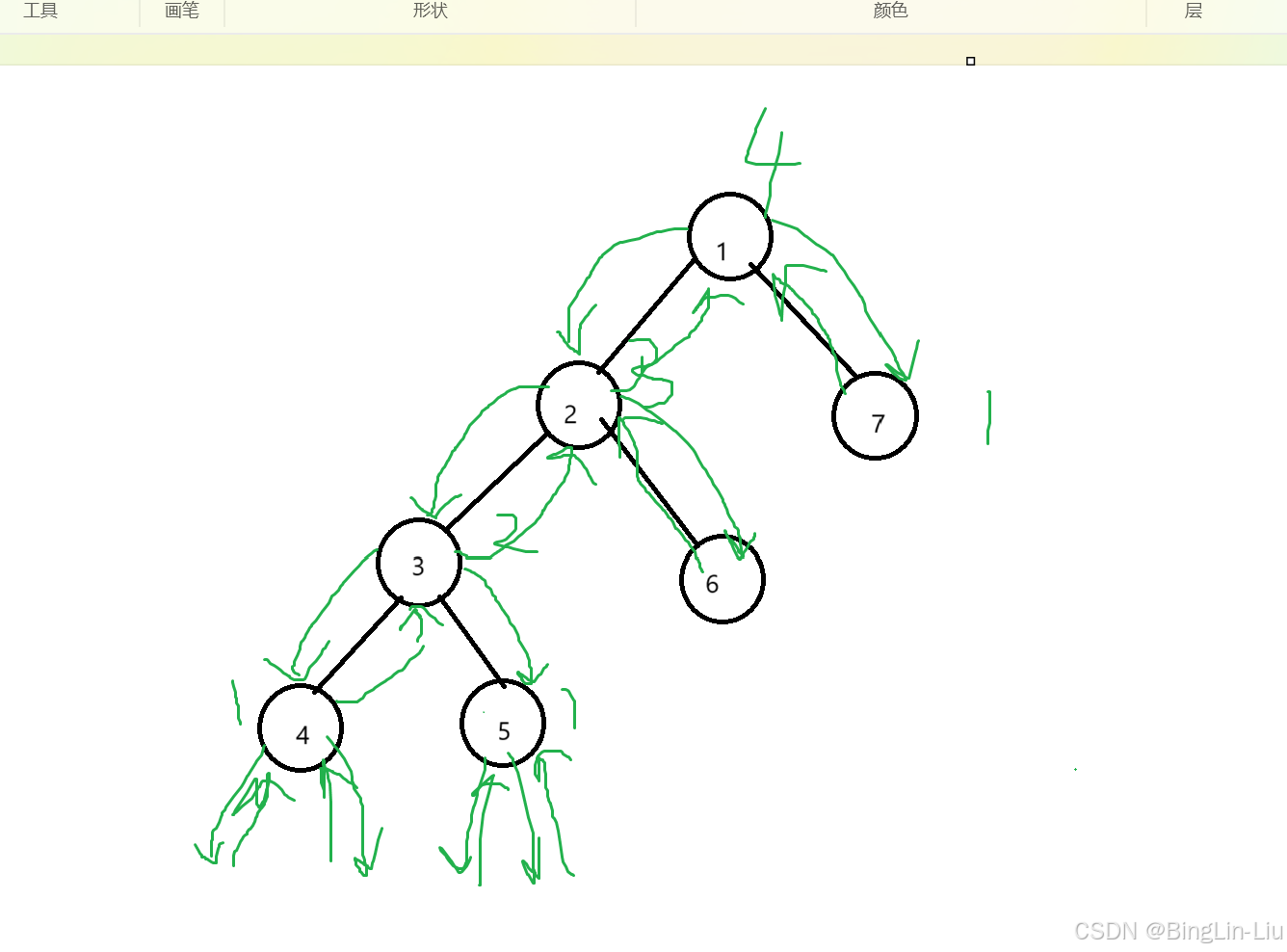
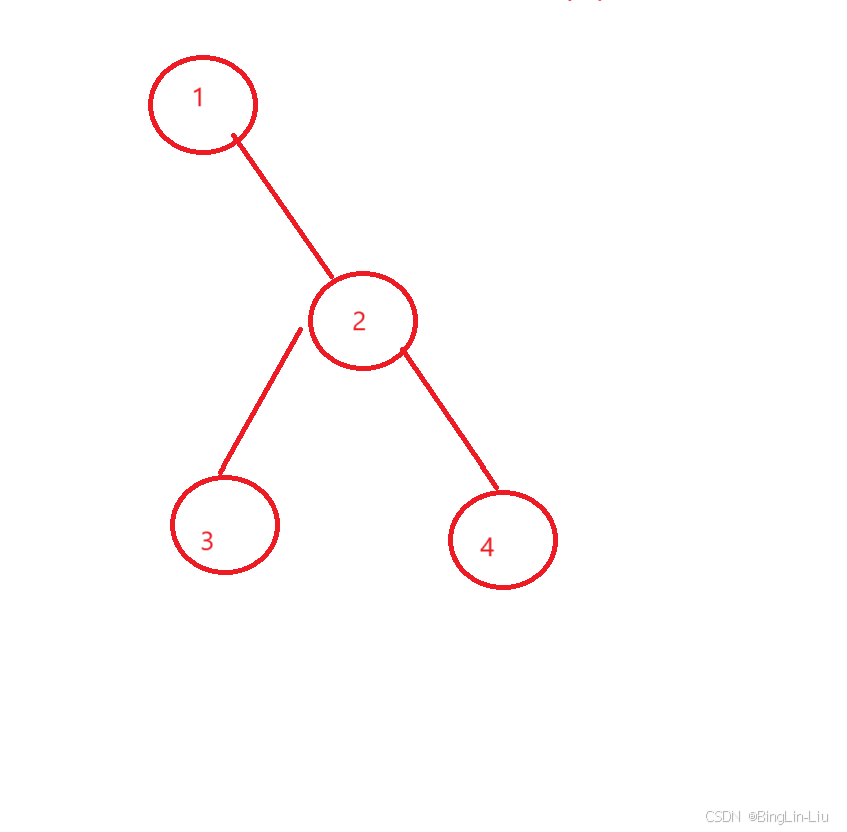
如果不是完全二叉树，我们也可以采用顺序存储，但是如果直接按层序遍历的下标存的话，我们用下标找孩子找父亲的时候就乱套了，这时候我们只需要把其他没有铺满的地方空出来就行，但是！我们假设一种极端情况如图，我们只需要存储四个结点，但是把它补全之后我们就要存储2的四次方-1 也就是15个结点，极大的浪费了我们的空间，所以我们最好只在满二叉树和完全二叉树的情况下用顺序存储

链式存储

链式存储类比链表的存储，有静态有动态，我们在竞赛里只需要掌握静态实现即可

竞赛中给的树一般都是有编号的，我们只需要实现一个足够大的数组，数组的下标表示树的编号，再实现两个数组l[N]和r[N]分别存储每个结点的左孩子和右孩子的编号

#include <iostream>
using namespace std;
const int N = 1e5 + 10;
int l[N], r[N];

int main()
{
	int n;
	cin >> n;
	for (int i = 1; i <= n; i++)
	{
		cin >> l[i] >> r[i];
	}



	return 0;
}

二叉树的遍历

深度遍历（先序，中序，后序）

不同于常规的树的遍历，二叉树由于其特殊的性质可以它的深度优先遍历可以分为先序，中序，后序

先序遍历就是先处理根节点----》再处理左子树 -----》再处理右子树

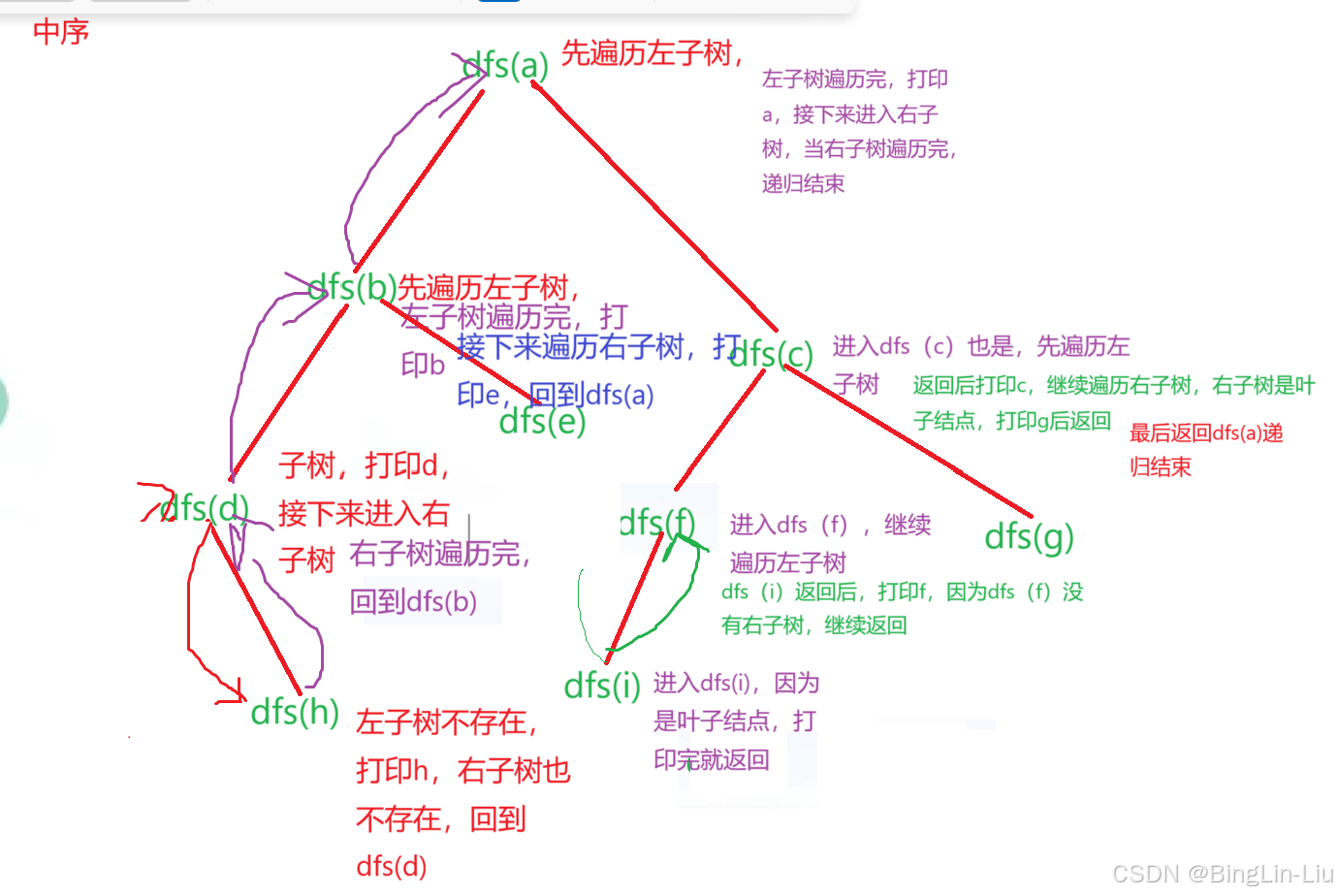
中序遍历就是先处理左子树----》再处理根节点------》再处理右子树

后序遍历就是先处理左子树----》再处理右子树-------》再处理根节点

如图，我们先序遍历一下这棵树，先序遍历序列就是 ABDEGCF

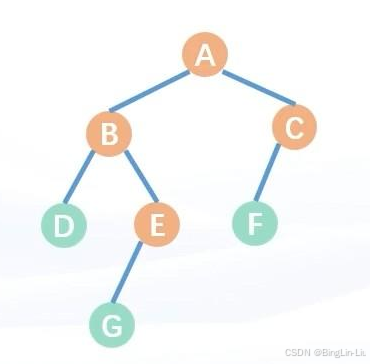
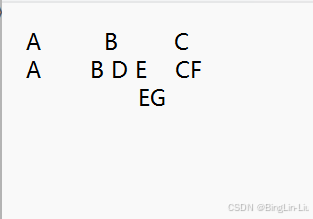
中序遍历就是也就是DBGEAFC

后序遍历就是DGEBFCA

接下来我们再用DFS的思想来遍历一下我们的二叉树

我们从根节点遍历的时候，先序遍历就是遍历一个节点打印一个节点，就是我们上一章树里面最常规的遍历方式中序遍历就是先遍历完左子树，再输出根节点，最后再遍历一遍右子树

后序遍历就是先遍历左子树，再遍历右子树，最后再输出根节点

这是我们的中序遍历

#include <iostream>
using namespace std;
const int N = 1e5 + 10;
int l[N], r[N];
void dfs1(int u)
{
	cout << u << " ";
	if(l[u])dfs1(l[u]);
    if(r[u])dfs1(r[u]);
}
void dfs2(int u)
{
	if (l[u])dfs2(l[u]);
	cout << u << " ";
	if (r[u])dfs2(r[u]);
}
void dfs3(int u)
{
	if (l[u])dfs1(l[u]);
	if (r[u])dfs1(r[u]);
	cout << u << " ";
}
int main()
{
	int n;
	cin >> n;
	for (int i = 1; i <= n; i++)
	{
		cin >> l[i] >> r[i];
	}
	dfs1(1);
	cout << endl;
	dfs2(1);
	cout << endl;
	dfs3(1);
	cout << endl;



	return 0;
}

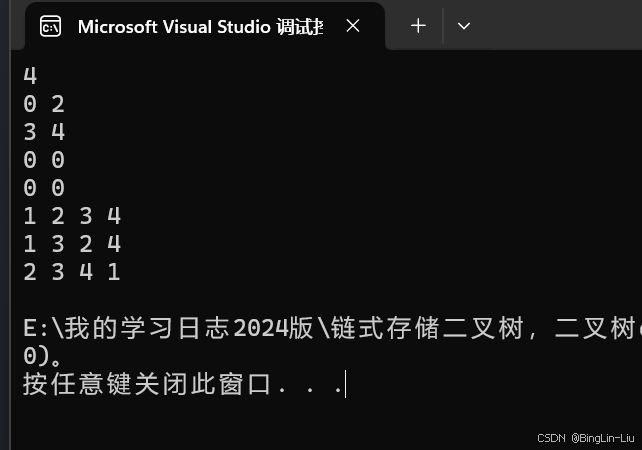
这是我们的代码

可以看出来，是符合的，我们接下来继续往下学习宽度遍历

宽度遍历

和上一章节的树一样，我们二叉树的宽度遍历也是用队列，队列出队的时候把孩子带进来，依次出队输出节点，就是我们的宽度遍历了

#include <iostream>
#include <queue>
using namespace std;
const int N = 1e5 + 10;
int l[N], r[N];
queue <int> q;
void bfs()
{
	q.push(1);
	while (q.size())
	{
		int u = q.front(); q.pop(); cout << u << " ";
		if (l[u]) q.push(l[u]);
		if (r[u]) q.push(r[u]);
	}
}
int main()
{
	int n;
	cin >> n;
	for (int i = 1; i <= n; i++)
	{
		cin >> l[i] >> r[i];
	}
	bfs();

	return 0;
}

二叉树相关算法题

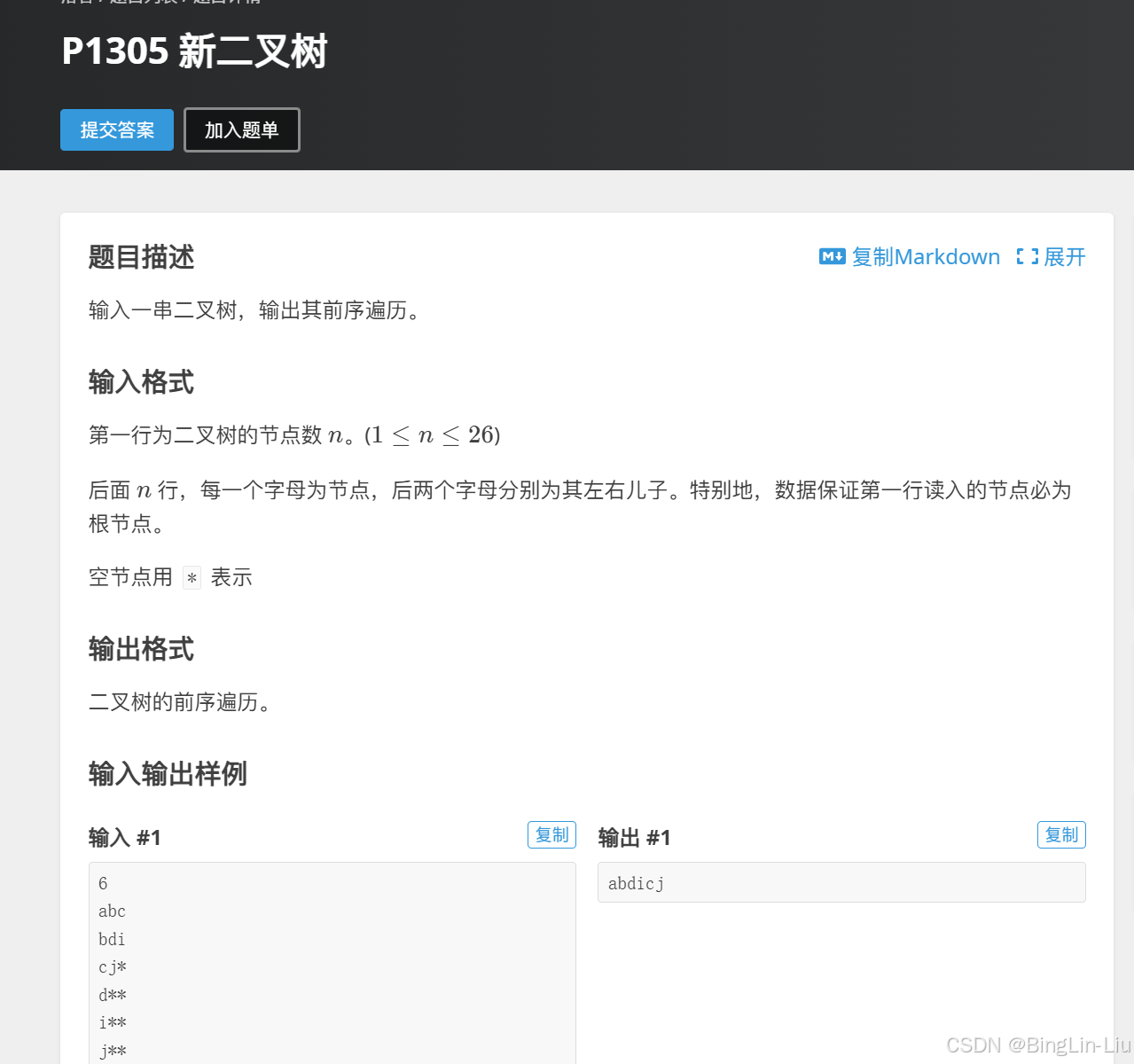
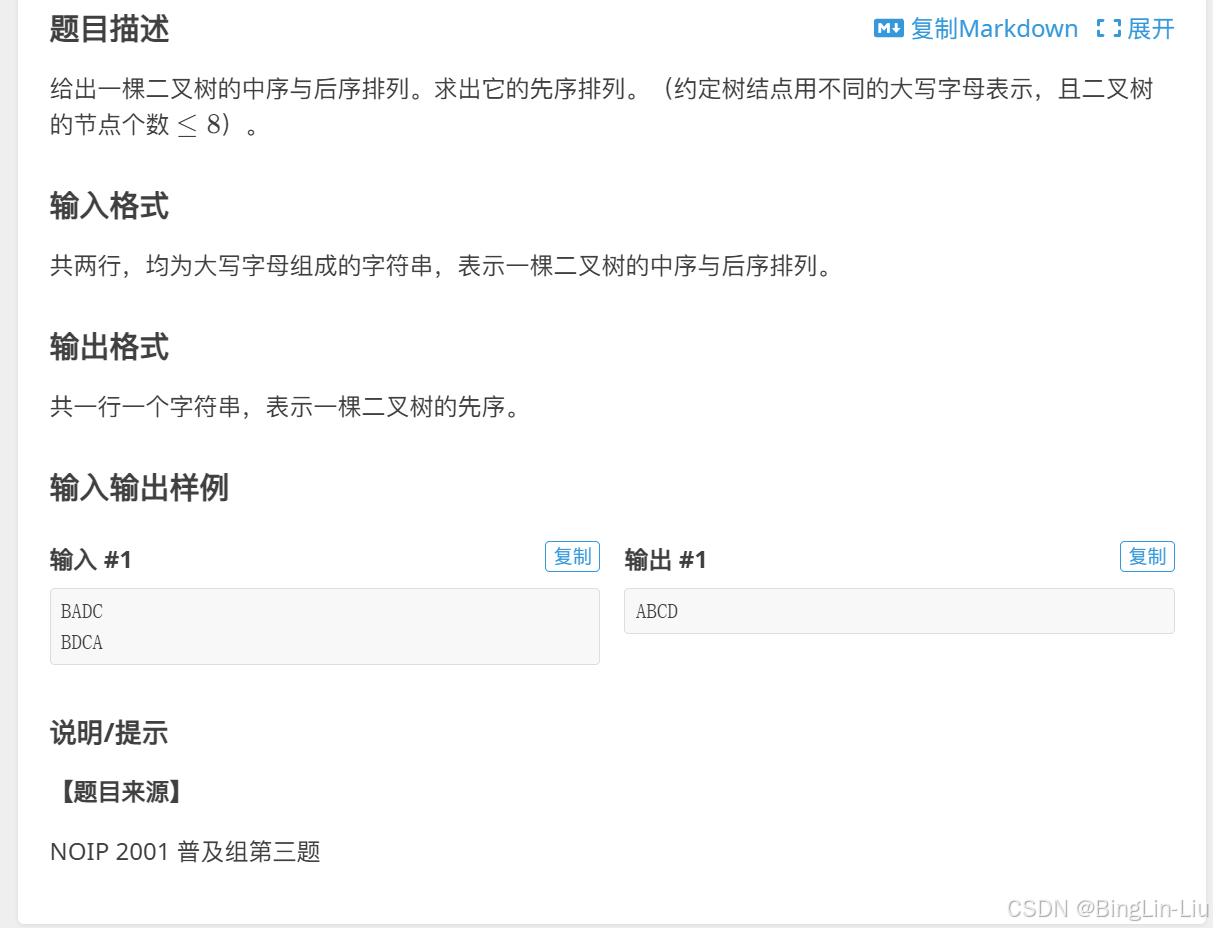
1.新二叉树

这道题就是简单的先序序列，只不过之前我们都是用1，2，3，4来表示结点，这里用的是abcdef字母来表示结点了

#include <iostream>
using namespace std;
const int N = 300;
char tree[N];
char l[N],r[N];
void dfs(char u)
{
	if(u == '*')
	return;
	cout << u ;
	dfs(l[u]);
	dfs(r[u]); 
}



int main()
{
	int n;
	cin >> n;
	char t;
	char root;
	cin >> root;
	cin >> l[root] >> r[root]; 
    for(int i = 2;i<=n;i++)
    {
    	char t; cin >> t;
    	cin >> l[t] >> r[t];
	}
	dfs(root);
	
	
	
	
	return 0;
}

2.二叉树的三种dfs遍历

#include <iostream>

using namespace std;
const int N = 1e6+10;
int l[N],r[N];
void dfs1(int u)
{
	if(!u) return;
	cout << u << " "; 
	dfs1(l[u]);
	dfs1(r[u]);
}
void dfs2(int u)
{
	if(!u) return;
	dfs2(l[u]);
	cout << u << " "; 
	dfs2(r[u]);
}
void dfs3(int u)
{
	if(!u) return;
	dfs3(l[u]);
	dfs3(r[u]);
	cout << u << " "; 

}



int main()
{
	int n;
	cin >> n;
	for(int i = 1;i<=n;i++)
      {
      	cin >> l[i] >> r[i];
      	
	  }
	dfs1(1);
	cout << endl;
	dfs2(1);
	cout << endl;
	dfs3(1);
	cout << endl;
	
	
	
	return 0;
}

3.二叉树的深度

二叉树的深度可以拆解成求h=max（左子树高度，右子树高度）+1

它是一个重复的子问题，我们可以用递归来解决

#include <iostream>
using namespace std;
const int N = 1e6+10;
int l[N],r[N];


int dfs(int root)
{
	if(!root) return 0;
	
	
	return max(dfs(l[root]),dfs(r[root])) + 1;
}
int main()
{
	int n;
	cin >> n;
	for(int i = 1;i<=n;i++)
	{
		cin >> l[i] >> r[i];
	}	
	cout << dfs(1) << endl;
	
	return 0;
}

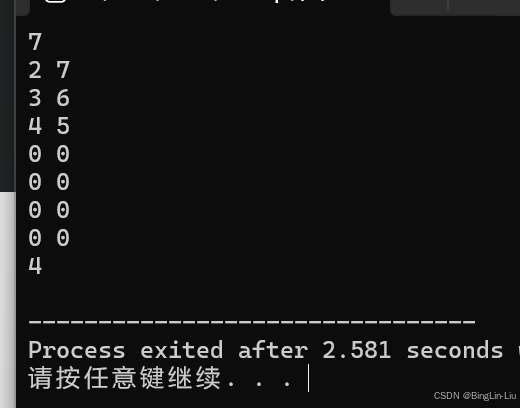
如图，和测试结果是一致的

4.以知中序和后序求先序

如图，中序序列是BADC 后序序列是BDCA，我们可以知道后序序列最后一个元素就是根结点，A就是根结点，那么中序序列可以分为两半儿，B是左子树，DC是右子树，然后先对左子树进行递归，再对右子树进行递归，每次都先输出根

注：后序序列的作用是找到根结点，中序序列的作用是区分左右子树

#include <iostream>
using namespace std;

string a,b;

void dfs(int l1,int r1,int l2,int r2)
{
	if(r1<l1)
	return;
	cout << b[r2];
	int p = l1;
	while(a[p] != b[r2])
	{
		p++;
	}
	dfs(l1,p-1,l2,l2+p-1-l1);
	dfs(p+1,r1,l2+p-l1,r2-1);
}


int main()
{
	cin >> a >> b;
	dfs(0,a.size()-1,0,b.size()-1);
	
	
}

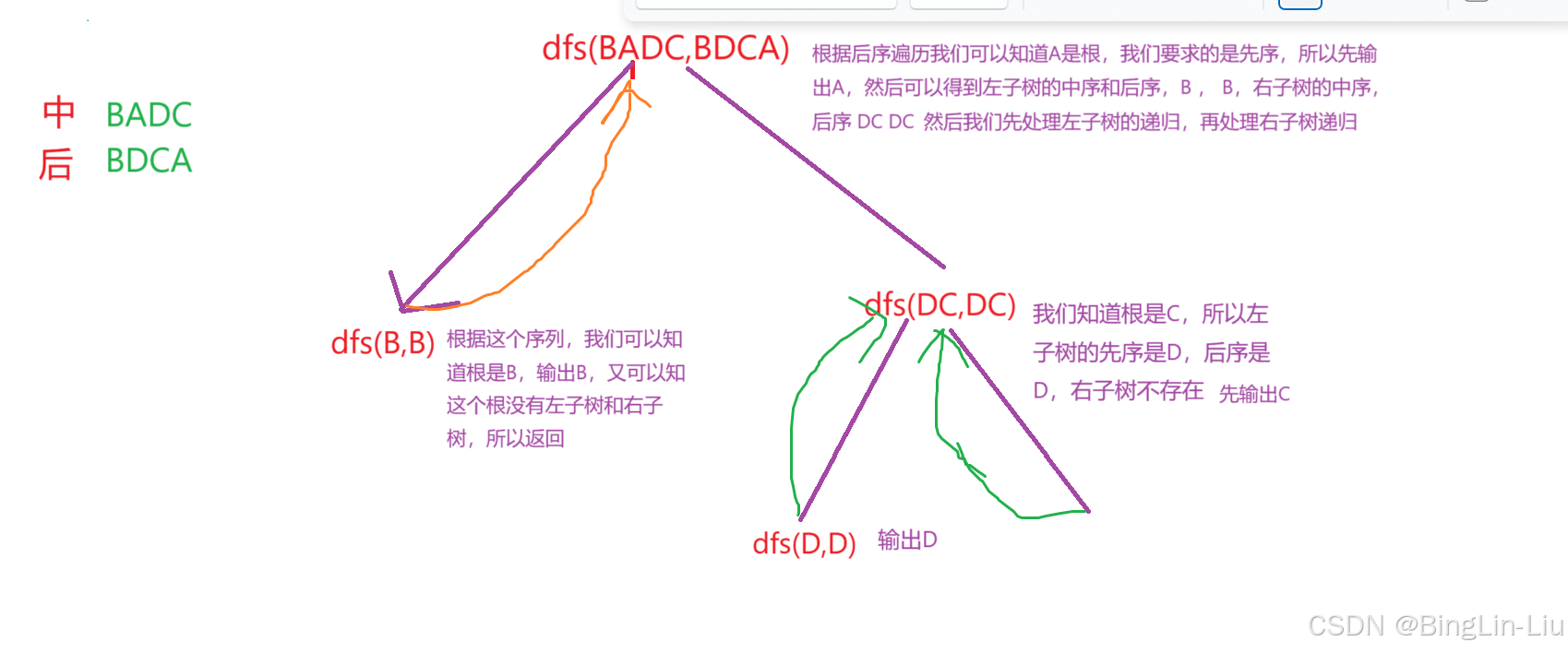
中序序列 BADC 后序序列BDCA

我们首先根据后序序列找到根结点，是A，然后通过中序序列，左子树是B，右子树是DC

然后我们先处理左子树，左子树的中序序列是B，后序也是B，所以根结点就是B，没有左右子树，所以就返回A是根结点时候的栈帧，继续处理右子树，右子树的中序是DC 后序也是DC，所以根结点是C，输出C，然后处理左子树先序是D，后序是D，根结点是D，输出D，返回C的栈帧，右子树不存在，返回A是根结点的栈帧，函数结束，递归完成。输出序列就是A，B，C，D

我们在真正写函数的时候用的是编号，我们可以通过画图来处理编号

5.已知中序和先序，求后序

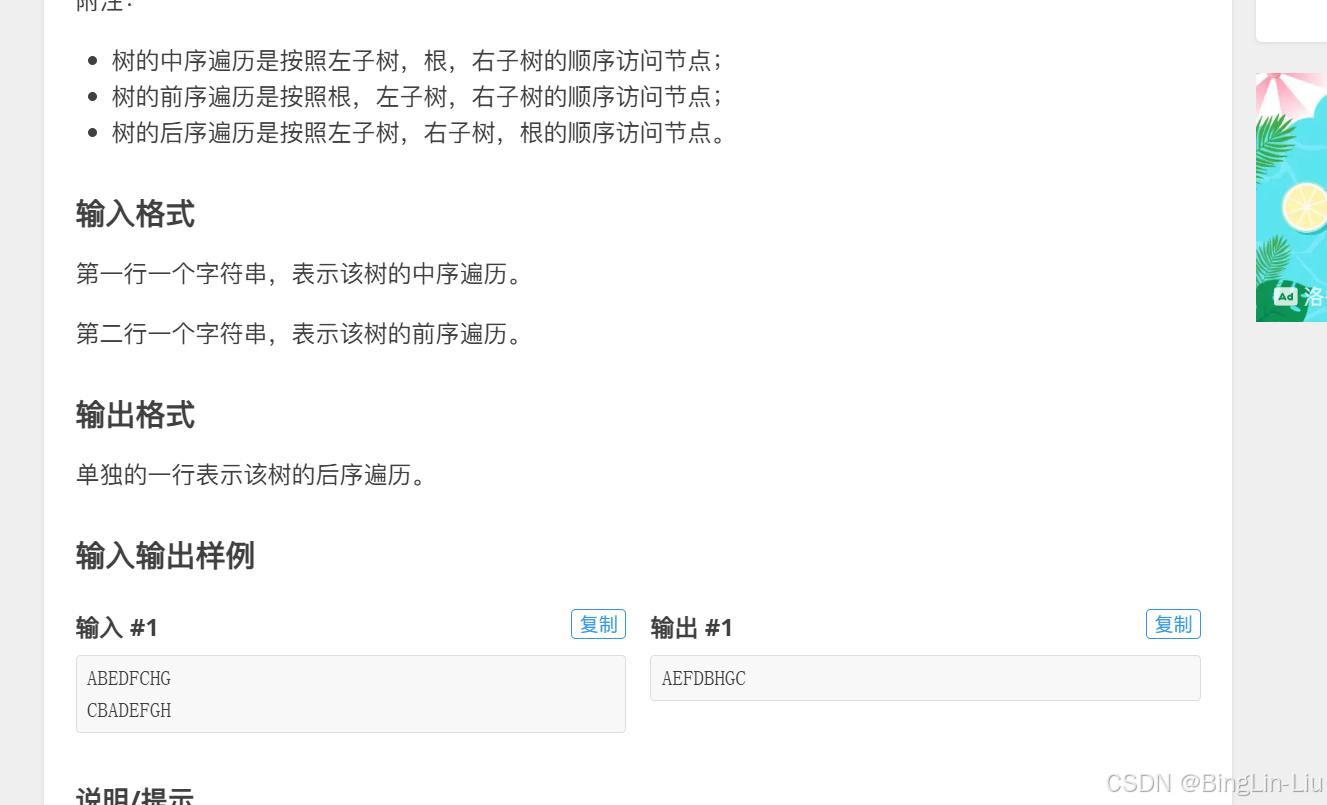
我们只要知道，后序和先序用来找根结点，中序用来划分左右子树，然后我们只要会写一趟的递归，其余的也就没问题了，下面就是我们的代码

#include <iostream>

using namespace std;
string s1,s2;
void dfs(int l1,int r1,int l2,int r2)
{
	if(l1>r1)
	return;
	int p = l1;
	while(s1[p] != s2[l2])
	{
		p++;
	}
	
	dfs(l1,p-1,l2+1,l2+p-l1);
	dfs(p+1,r1,l2+p-l1+1,r2);
	
	cout << s1[p];
	
	
	
}

int main()
{
	cin >> s1 >> s2;
	dfs(0,s1.size()-1,0,s2.size()-1);
	
	
	return 0;
}

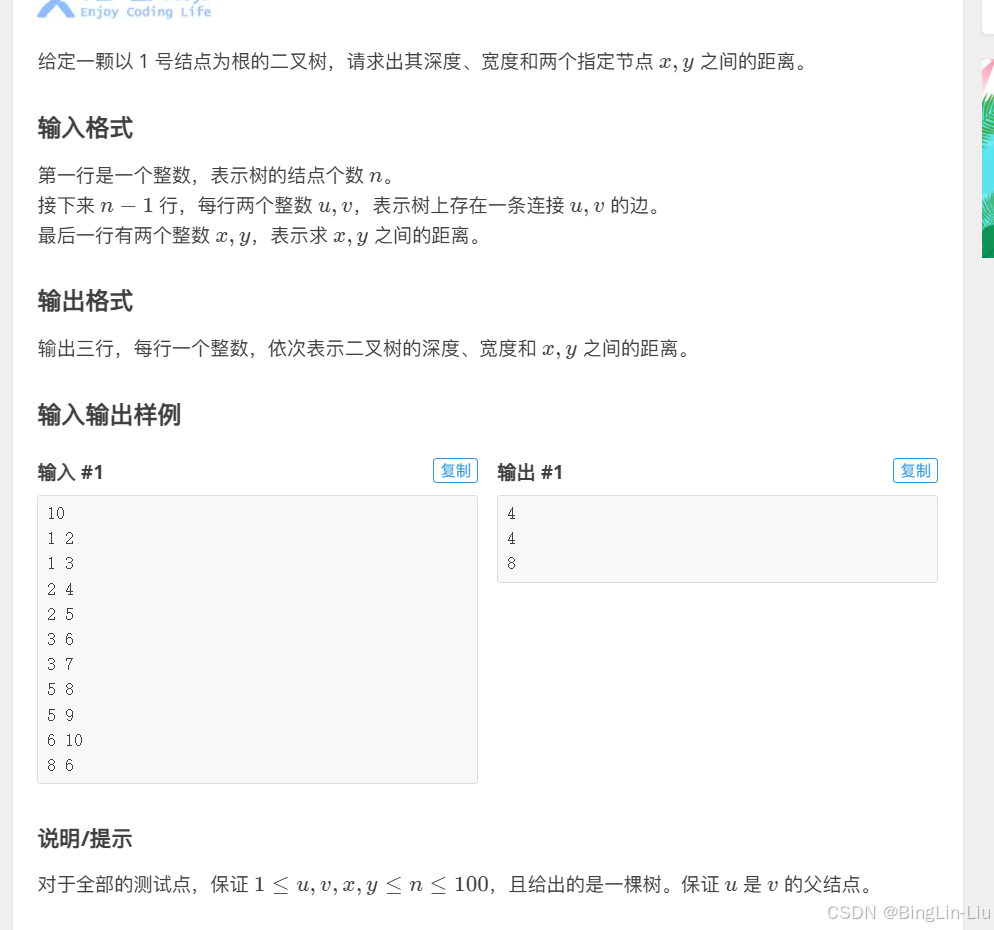
6.树的深度，宽度，以及两个结点x和y之间的距离

#include <iostream>
#include <vector>
#include <queue>
using namespace std;

const int N = 110;
vector <int> edges[N];

int dfs(int u)
{
	if(u == 0)
	return 0;
	int max1 = 0;
    for(auto e : edges[u])
    {
    	max1 = max(max1,dfs(e));
	}
	return max1+1;
}
int bfs()
{
	queue<int> q;
	q.push(1);
	int ret = 0;
	while(q.size())
	{
		int sz = q.size();
		ret = max(sz,ret);
	    while(sz--)
	    {
	    	int t = q.front();q.pop();
	    	for(auto v : edges[t])
	    	{
	    		q.push(v);
			}
		}
	}
	return ret;
}
int fa[N];//用来找到i结点的父亲 
int dist[N];//用来标记i结点到x结点的距离
int len = 0;//用来记录y结点向上爬的时候和x结点爬的路线相交的距离
//当我们求结点最短距离的时候，就用dist[相遇结点]再加上len就行了 
int main()
{
	int n;
	cin >> n;
	int u,v;
	
	for(int i = 1;i<n;i++)
	{
         cin >> u >> v;
         edges[u].push_back(v);
         fa[v] = u; 
	}
	int x,y;
	cin >> x >> y;
	while(x!=1)
	{
		dist[fa[x]] = dist[x] +1;
		x = fa[x];
	}
   while(y!=1 && dist[y] == 0)
	{
		
		y = fa[y];
		len++;
	}
	cout << dfs(1) << endl;
	cout << bfs() << endl;
	cout << 2*dist[y] + len << endl;
	return 0;
}