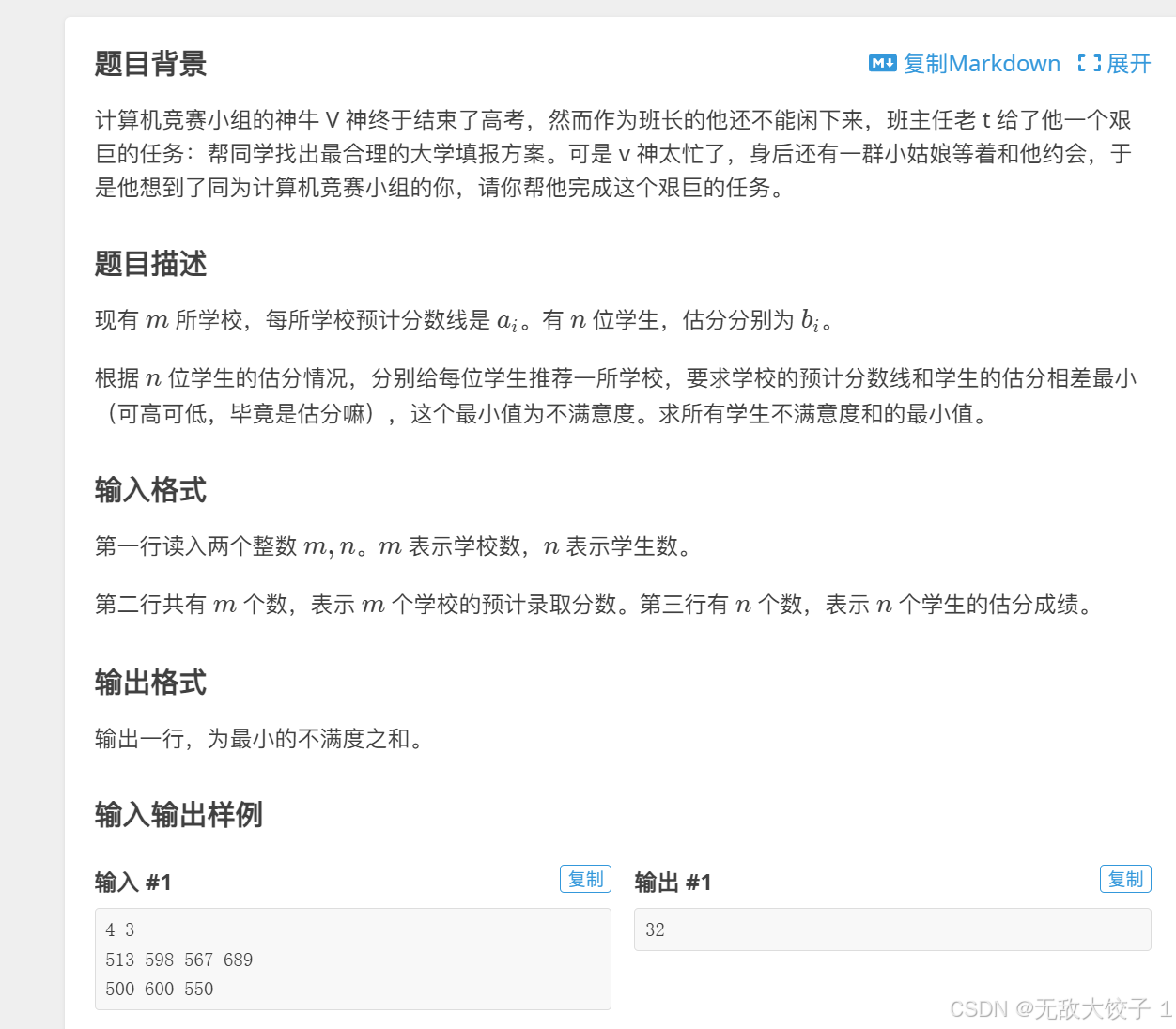
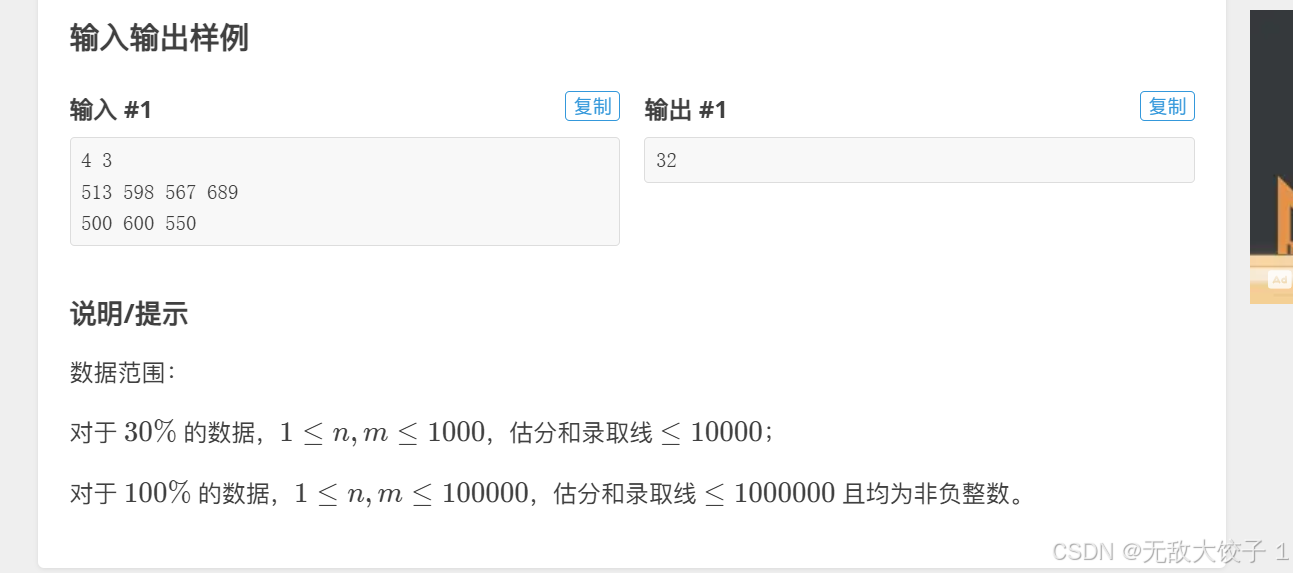
这道题我们把学校录取分数线存在数组里并且排序，然后枚举学生实际分数，用二分查找找出大于等于实际分数的最初位置，该位

#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1e6 + 10;
typedef long long LL;
int a[N];
int m, n;
int find(int x)
{
	int left = 1, right = m;
	while (left < right)
	{
		int mid = left + (right - left) / 2;
		if (a[mid] >= x) right = mid;
		else left = mid + 1;
	}
	return left;
}
int main()
{
	cin >> m >> n;
	LL ret = 0;
	for (int i = 1; i <= m; i++) cin >> a[i];
	a[0] = -1e7;
	sort(a + 1, a + 1 + m);
	while (n--)
	{
		int x; cin >> x;
		int pos = find(x);
		ret += min(abs(a[pos] - x), abs(a[pos - 1] - x));
	}
	cout << ret << endl;

	return 0;
}

置减1就是小于它的最终位置，然后比较这两个位置的值哪个和实际分数最接近，如果数组就一个元素的话就会发生越界，这时候我们只要安一个左护法就行了，左护法多大呢？假如我们的分数是10的六次方的话，预估分数是0的话，最多差值就是10的六次方，我们只要让左护法比10的六次方大就行了