✨感谢您阅读本篇文章,文章内容是个人学习笔记的整理,如果哪里有误的话还请您指正噢✨
✨ 个人主页:余辉zmh–CSDN博客
✨ 文章所属专栏:贪心算法篇–CSDN博客
前言
本篇文章是对贪心算法练习题的讲解,有关贪心算法的讲解可以看本系列的第一篇文章,这里就不再重复讲解,直接继续讲解例题。
例题
1.买卖股票的最佳时机
题目:
算法原理:
本道题的贪心策略很简单,既然要求获取最高的利润,而且本道题限制只能买卖一次,那么就在整个股票价格中选择最低点买入,最高点卖出即可,这样就能保证利润最大化。
设置两个变量,一个用来标记最低的买价,一个用来标记当前利润;遍历整个股票价格,现将当前价格减去最低的买价更新利润,然后更新当前价格是否是最低价。遍历完整个股票价格后,当前利润就是最大的利润。
代码实现:
int maxProfit(vector<int>& prices){
//minnum表示最低的买价,ret表示最高的利润
int minnum = INT_MAX, ret = INT_MIN;
for(auto x : prices){
ret = max(ret, x - minnum);
minnum = min(minnum, x);
}
if(ret<0){
return 0;
}
return ret;
}
2.买卖股票的最佳时机2
题目:
算法原理:
本道题和上一道题不同的是,不再局限于只能买卖一次,可以无限次买卖,只要保证最后的利润是最大的即可。
首先需要明白,什么时候买卖才能有利润不亏损,那就是下一个价格比当前价格低,也就是升序排列,所以在上升趋势段买卖,才会有利润,但是在上升趋势段的什么时候买卖才能最大利润,那肯定就是上升趋势段的最低点和最高点买入和卖出。因此找到所有升序段的利润然后相加就是整体的最大利润。这就是本道题的贪心策略。
这里有两种解法:第一种就是找到一个升序段,标记最低点和最高点的价格,然后直接两个端点相减就是当前整个升序段的利润和;第二种就是只要下一个的价格大于当前价格,就买入和卖出。比如说当前有连续三天的价格都是上升趋势,第一种方式就是在第一天买入,第三天卖出,只找开始和结尾。而第二种方式则是,第一天买入,第二天卖出,然后第二天再买入,第三天卖出,将整个升序段的利润拆分成每一天利润,最后每一天的利润和还是整个升序段的利润和。
代码实现:
//方法一:
int maxProfit(vector<int>& prices){
//使用双指针找到上升趋势的最低点和最高点进行买卖
int ret = 0;
for (int buy = 0; buy < prices.size(); buy++){
//卖指针从买指针位置开始找
int sell = buy;
//找到上身趋势的最高点
while(sell+1<prices.size()&&prices[sell]<prices[sell+1]){
sell++;
}
//在当前位置买卖
ret += prices[sell] - prices[buy];
//更新买指针指向当前位置
buy = sell;
}
return ret;
}
//方法二:
int maxProfit(vector<int>& prices){
//在上升趋势段,一天一天地买卖获取利润
int ret = 0;
for (int i = 0; i < prices.size(); i++){
//如果下一个值大于当前值,就直接买卖
if(i+1<prices.size()&&prices[i+1]>prices[i]){
ret += prices[i + 1] - prices[i];
}
}
return ret;
}
3.k次取反后的最大化数组和
题目:
算法原理:
本道题的题意要求,挑选数组中的一个数变化为相反数,总共需要变化k次,最后使变化后的数组和最大。注意一个数可以变化多次,没有次数限制。
既然题意要求变化后的数组和最大,那么每次变化都挑选最小的数变化不就行了吗,这样就能对数组和的影响减小。但是数组中有正数和负数之分,因此两种情况要分类讨论:如果是负数的话,负数的相反数是正数,可以使数组和变大,因此负数只需变化一次即可;如果是正数的话,还要继续分情况讨论:如果当前剩余的k次为偶数,正数变化两次后还是正数,所以变化偶数次后还是当前数,相当于不变,对数组和无影响直接结束;如果当前剩余的k次为奇数,只需让最小的正数变化一次为负数,这样对数组和的影响最小,然后剩余偶数次,变化偶数次后相当于不变,直接结束即可。这就是本道题的贪心策略。
这里我是用小根堆数据结构来实现,每次直接获取堆顶元素,然后判断正负,负数就变化一次,变化后存放到堆中,正数再判断剩余次数的奇偶,如果是偶数,直接结束,相当于变化偶数次不变;如果是奇数,当前正数因为是最小的正数所以变化一次,剩余偶数次,同理直接结束。最后返回变化后的元素和
代码实现:
struct Greater{
bool operator()(const int p1,const int p2){
return p1 > p2;
}
};
int largestSumAfterKNegations(vector<int>& nums, int k){
//建立一个小根堆
priority_queue<int, vector<int>, Greater> heap(nums.begin(), nums.end());
while(k>0){
//获取堆顶元素
int t = heap.top();
heap.pop();
//如果堆顶元素是负数,修改为正数
if(t<0){
heap.push(-t);
k--;
}
//如果堆顶元素是正数,先判断当前剩余次数
else{
//如果次数为奇数,修改最小的正数为负数,次数减一,剩余次数就是偶数
//下一个正数进行偶数次的变换,相当于不变,直接结束
if(k%2==1){
heap.push(-t);
k = 0;
}
//如果剩余偶数次,当前正数变化完所有次数,相当于不变,直接结束
else{
heap.push(t);
k = 0;
}
}
}
int ret = 0;
while(!heap.empty()){
ret+=heap.top();
heap.pop();
}
return ret;
}
4.按身高排序
题目:
算法原理:
本道题其实并不是贪心算法题,但是本道题使用的策略会在下一道贪心算法题中用到,因此可以先用这道题练习一下。
本道题就是一道简单的排序问题,一个数组存放的是名字,一个数组存放的是身高,两个数组通过下标可以一一对应名字和身高,然后就是按照身高排序,返回排序后的名字。这里就存在了一个细节问题,如果直接对身高这个数组排序,排完序后,名字数组没有变,就会导致不能再通过下标一一对应名字和身高,最后返回的名字顺序也就是错误的。
本道题有多种解法,第一种就是可以使用二元数组,重新创建一个数组,数组里面存放的是键值对pair<string,int>,使每个名字一一对应各自的身高。然后将数组按照身高排序,最后遍历数组返回名字即可。第二种就是可以借助哈希表,建立名字和身高的映射关系,其实和第一种同理,只不过数据存储方式不一样,实现过程还是相同的。
上面两种方式都可以实现,但这里重点要介绍的还是第三种方式:直接对下标进行排序,建立一个新数组,存放的是每一个下标,然后通过Lambda表达式自定义排序规则,[&]是捕获列表,用于排序时可以访问的外部变量,这里排序的外部变量就是身高数组;()内是参数列表,对应下标数组中需要排序的两个下标;{}内是函数体,也就是排序规则的实现,按照下标对应的身高数组中的身高进行排序。这样自定义排序规则就可以实现下标按照身高排序,不改变原有的名字和身高数组,最后再遍历排序好的下标数组,通过下标就可以找到名字,返回即可。
代码实现:
vector<string> sortPeople(vector<string>& names, vector<int>& heights){
//建立一个下标数组
int n = names.size();
vector<int> index(n);
for (int i = 0; i < n; i++){
index[i] = i;
}
//对下标数组进行排序
sort(index.begin(), index.end(), [&](const int i, const int j){
return heights[i] > heights[j];
});
//提取结果
vector<string> ret;
for(auto i : index){
ret.push_back(names[i]);
}
return ret;
}
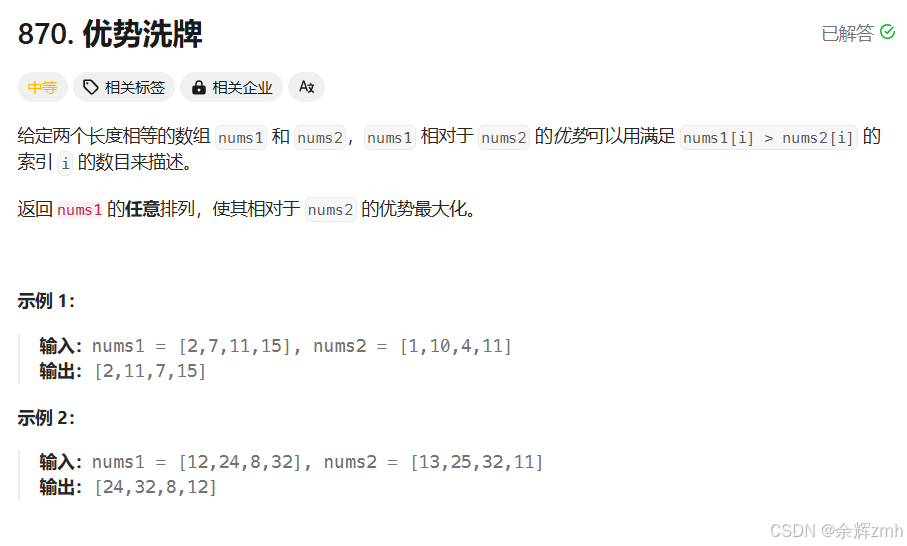
5.优势洗牌
题目:
算法原理:
代码实现:
vector<int> advantageCount(vector<int>& nums1, vector<int>& nums2){
int n = nums1.size(), m = nums2.size();
//给数组2创建一个下标数组
vector<int> index(m);
for (int i = 0; i < m; i++){
index[i] = i;
}
// 数组1直接排序,数组2通过下标数组排序,排升序
sort(nums1.begin(), nums1.end());
sort(index.begin(), index.end(), [&](const int i, const int j) {
return nums2[i] < nums2[j];
});
//创建一个结果数组用来存放数组1按题意要求的排序
vector<int> ret(n);
//两个指针用来指向下标数组的前后位置
int left = 0, right = m - 1;
for (int i = 0; i < ; i++){
//如果第一个数组的值大于第二个数组的当前值,左指针指向下标数组中的位置就是结果数组中存放的下标
if(nums1[i]>nums2[index[left]]){
ret[index[left++]] = nums1[i];
}
//如果小于等于,存放到右指针指向的下标位置
else{
ret[index[right--]] = nums1[i];
}
}
return ret;
}
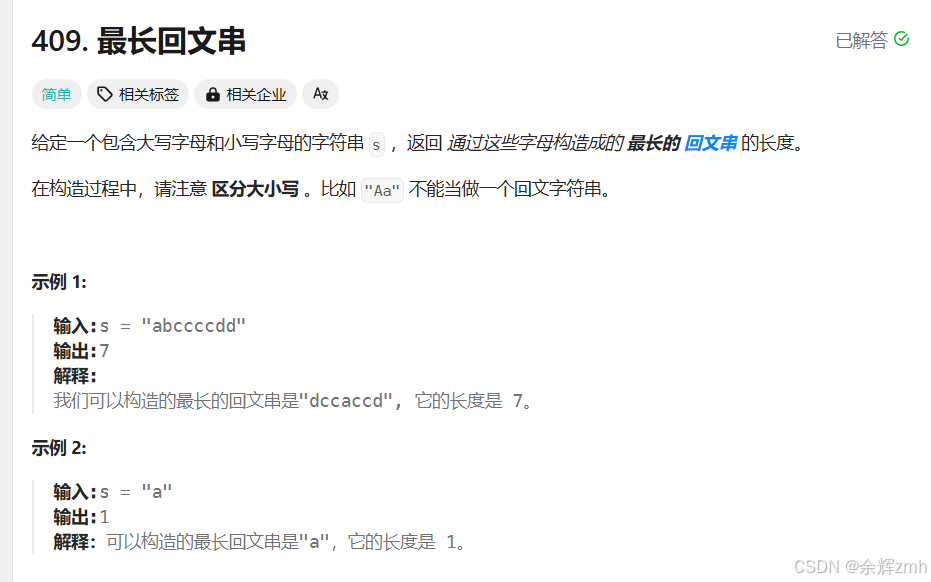
6.最长回文串
题目:
算法原理:
本道题的贪心策略比较简单,构成回文串时尽可能多地选取字符,先统计所有字符的个数,有奇数个也有偶数个,如果当前字符是偶数个n,那么回文串中一定包含所有的当前字符n个,比如字符a有4个,回文串就是aa|aa,左右两侧平均分;如果当前字符是奇数个n,那么回文串中一定包含当前字符的n-1个,比如字符b有5个,回文串就是bb|bb;当统计完所有字符后,如果最后回文串的长度小于原字符串的长度,说明存在奇数个字符,随便选一个奇数个的字符放到中间|位置,回文串的长度再加一。
代码实现:
int longestPalindrome(string s){
//建立哈希表,统计字符的个数
unordered_map<char, int> hash;
for(auto ch : s){
hash[ch]++;
}
int ret = 0;
for(auto& [ch,count] : hash){
//不管个数是奇数还是偶数,都是先除以2再乘以2
ret += count / 2 * 2;
}
//如果最后回文串的长度小于原字符串的长度,说明存在奇数个的字符,回文串长度再+1
if(ret<s.size()){
ret++;
}
return ret;
}
7.增减字符串匹配
题目:
算法原理:
本道题的贪心策略:原字符串的长度为n,从0到n挑选数字填充数组对应字符串中的每个字符,遇到’I’选择0到n中剩余的最小的数,因为下一个不管位置是字符’I’还是字符’D’,挑选的值都会比当前最小的数大,这样就能满足字符’I’的要求,下一个比当前的大;遇到’D’选择0到n中剩余的最大的数,因为下一个不管位置时字符’I’还是字符’D’,挑选的值都会比当前最大的数小,这样就能满足字符’D’的要求,下一个比当前的小,当遍历完所有的字符后,剩下的一个值填充到数组最后。
代码实现:
vector<int> diStringMatch(string s){
//贪心策略:遇到'I'选择最小的数,遇到'D'选择最大的数
int n = s.size();
//两个指针表示0到n的数字,left表示最小的数,right表示最大的数
int left = 0, right = n;
vector<int> ret(n + 1);
for (int i = 0; i < n; i++){
if(s[i]=='I'){
ret[i] = left++;
}
else{
ret[i] = right--;
}
}
//最后一个位置用剩下的一个值填充
ret[n] = left;
return ret;
}
8.分发饼干
题目:
算法原理:
本道题的贪心策略其实和上面优势洗牌一样,同样借助了田忌赛马的原理,只不过本道题比较简单,要求统计的是最多能满足的个数,不用按照数组的格式一一对应返回,所以贪心策略就可以简单化,还是先将两个数组排序然后一一比较,如果两个数能比过,也就是数组s的值大于数组g的值就直接比较下一对,满足个数加一;如果比不过,也就是数组s的值小于数组g的值,不用再和数组g中最大的值比较去拖累最大的值,因为即使和最大的比较也比过,题意要求返回的是满足个数,所以直接跳过当前数组s的值,用下一个比即可。
相较于优势洗牌那道题,本道题还是比较简单的。
代码实现:
int findContentChildren(vector<int>& g, vector<int>& s){
//贪心策略,先将两个数组排序,在能满足当前胃口的情况下选择较小的饼干
sort(g.begin(),g.end());
sort(s.begin(), s.end());
int ret = 0;
for (int i = 0, j = 0; i < g.size() && j < s.size(); ){
//如果当前饼干能满足当前胃口值,直接选择当前饼干
if(s[j]>=g[i]){
ret++;
i++;
j++;
}
//否则,跳过当前饼干
else{
j++;
}
}
return ret;
}
以上就是关于贪心算法练习题第二部分的讲解,如果哪里有错的话,可以在评论区指正,也欢迎大家一起讨论学习,如果对你的学习有帮助的话,点点赞关注支持一下吧!!!