目录
1.常数时间的操作
一个操作如果和样本的数据量无关,每次都是固定时间内完成的操作,叫做常数操作
时间复杂度为一个算法流程中,常数数量的一个指标,常用O来表示。具体来说,先要对一个算法流程非常熟悉,然后去写出这个算法流程中发生了多少次常数操作,进而总结出常数操作数量的表达式
在表达式中,只要高阶项,不要低阶项,也不要高阶项的系数,剩下的部分如果为f(N),那么时间复杂度为O(f(N))
评价一个算法流程的好坏,先看时间复杂度的指标,然后再分析不同样本数据下的实际运行时间,也就是“常数项时间”
- 常数操作:int a = arr[i]; 或 +-*/ 或 位运算 等
- 非常数操作:int b = 链表.get(i);
2.时间复杂度
2.1.以选择排序为例
时间复杂度O(N^2),额外空间复杂度O(1)
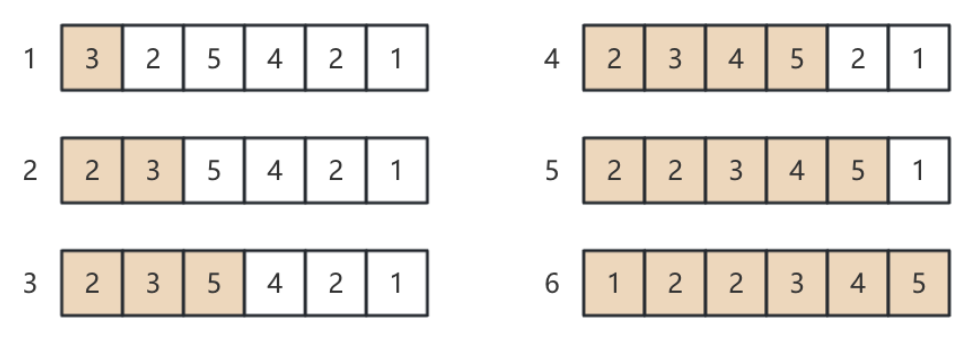
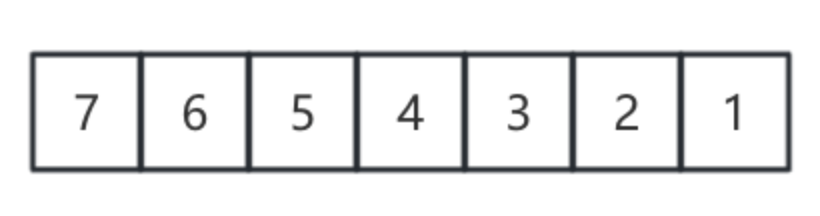
设数组长度为N,我们遍历N次,每次把遍历到的最小值放在最左边的位置上,同时把左边界向右移动一位
我们每一次找出最小的数、次小的数、次次小的数...待寻找的区间不断被压缩
这是一种基础且低效的查找方式,它的时间复杂度是O(n^2)
2.2.O(n^2)从何而来
数一数一共进行了多少次常数操作
第一次遍历时,遍历了N次,比较了N次,交换了1次
第二次遍历时,遍历了N-1次,比较了N-1次,交换了1次
......
遍历:N + N-1 + N-2 + N-3 + ...
比较:N + N-1 + N-2 + N-3 + ...
swap:N次
三者相加 = aN^2 + bN + c只要高阶项为N^2
2.3.冒泡排序
时间复杂度O(N^2),额外空间复杂度O(1)
相邻两个数字进行比较,大的数字往右移,一共遍历N-1次,第一次从第1个元素开始与相邻后一个元素比较,直到第N-1个元素与第N个元素比较完为止,此时当前数组中最大的元素一定被排序到了最后一位。接着继续遍历前N-1个元素,第二次遍历结束后,前N-1个元素的最大值一定被排序到了倒数第二位...
public static void bubbleSort(int[] arr) {
if (arr == null || arr.length < 2) {
return;
}
for (int e = arr.length-1; e > 0; e--) {
for (int i = 0; i < e; i++) {
if (arr[i] > arr[i+1]) {
swap(arr, i, i+1);
}
}
}
}
//交换arr的i和j位置上的值
public static void swap(int[] arr, int i, int j) {
arr[i] = arr[i] ^ arr[j];
arr[j] = arr[i] ^ arr[j];
arr[i] = arr[i] ^ arr[j];
}2.3.1.抑或运算
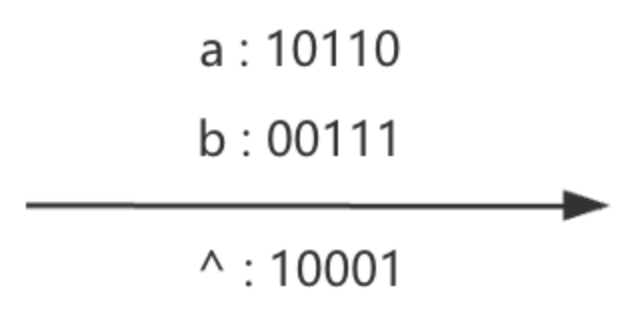
相同为0,不同为1
抑或运算还可以理解为无进位相加
- 抑或运算的性质
(1) 0^N=N N^N=0
(2) 交换律:a^b = b^a
结合律:(a^b)^c = a^(b^c)
(3)同一批数进行抑或结果永远相同
//怎么交换两个数的值
a = a^b;
b = a^b; //即b = (a^b)^b = a^(b^b) = a^0 = a
a = a^b;a和b的值可以相等,但这样做的前提是a与b在内存里是两块独立的区域,在数组中两个指针所指向的位置不能相同
- 与抑或有关的面试题
(1)
在一个数组中只有一种数出现了奇数次,其他的所有数都出现了偶数次,怎么找到出现了奇数次的数?要求时间复杂度O(N),空间复杂度O(1)
答:
int eor = 0;
for (int cur : arr) {
eor ^= cur;
}
return eor;(2) 在一个数组中只有两种数出现了奇数次,其他的所有数都出现了偶数次,怎么找到出现了奇数次的数?要求时间复杂度O(N),空间复杂度O(1)
- 为什么抑或运算满足交换律与结合律
用“无进位相加”解释:一组二进制数相加的结果与什么有关,与在某个二进制位上1的个数有关,与这些1出现的次序无关。在无进位相加时,偶数个1相加的结果是0,奇数个1相加的结果是1
//假设两种出现奇数次的数是a、b,a!=b
int eor = 0;
for (int cur : arr) {
eor ^= cur;
}
//eor == a^b != 0 => eor一定在某一位上等于1(int32位)
//假设eor的第x位为1
int eor_ = 0;
for (int cur : arr) {
if (cur的第x位等于0) {
eor_ ^= cur;
}
}
//eor == a 或 eor == b 而另一个数则是eor^eor_现在的问题是,eor的第几位是1?
我们选择最右侧的1
//找到eor最右侧的1
int rightOne = eor & (~eor + 1);
//cur的第x位为0这样表示
cur & rightOne == 0;2.4.插入排序
时间复杂度O(N^2),额外空间复杂度O(1)
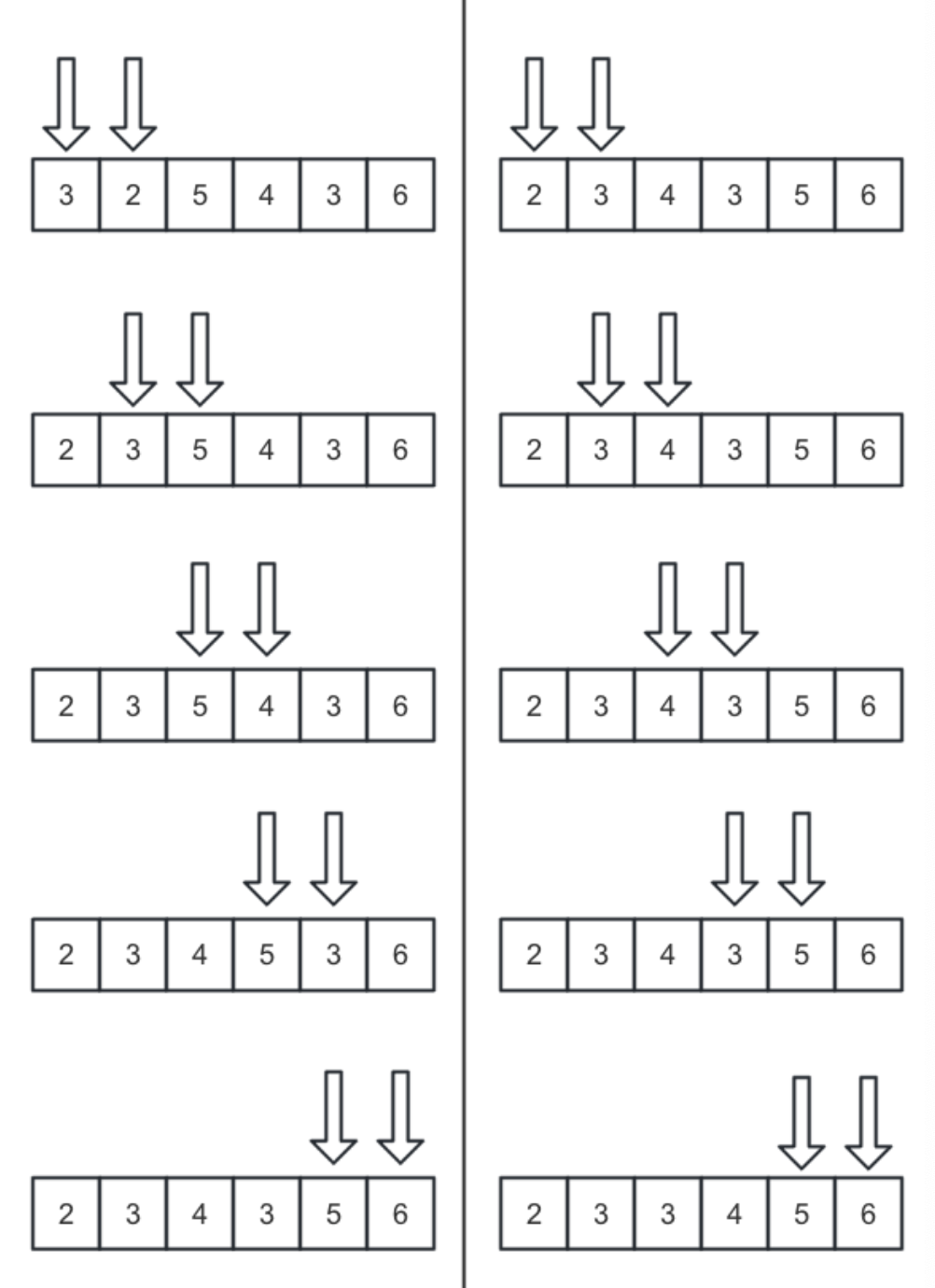
一共排序N = arr.length次,第一次排序前1个数,第二次排序前2个数...每次都把当前范围内最右边的数向左移,直到左边的数小于当前数字为止,此时该范围内的数必定有序
对于不同的数据,插入排序的时间复杂度不同
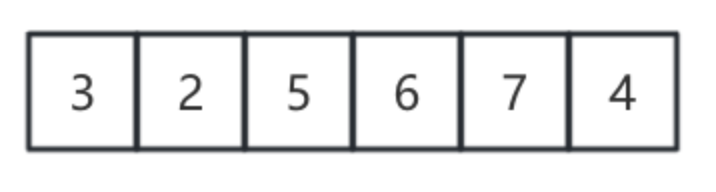
假如数据如下
时间复杂度为O(N^2)
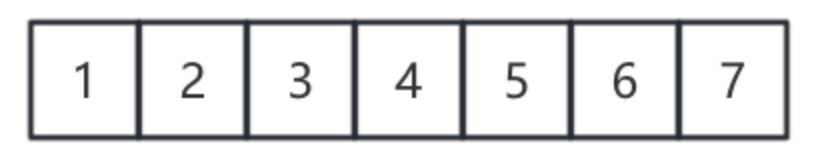
假如数据如下
时间复杂度为O(N)
我们约定,时间复杂度是最坏情况下的算法表现,所以插入排序的时间复杂度是O(N^2)
public static void insertionSort(int[] arr) {
if (arr == null || arr.length < 2) {
return;
}
for (int i = 1; i < arr.length; i++) { //0~i做到有序
for (int j = i-1; j >= 0 && arr[j] > arr[j+1]; j--) {
swap(arr, j, j+1);
}
}
}
public static void swap(int[] arr, int i, int j) {
arr[i] = arr[i] ^ arr[j];
arr[j] = arr[i] ^ arr[j];
arr[i] = arr[i] ^ arr[j];
}3.二分法
一个有序数组找某个数是否存在
如果遍历,算法时间复杂度O(N),没有用到有序这一特性
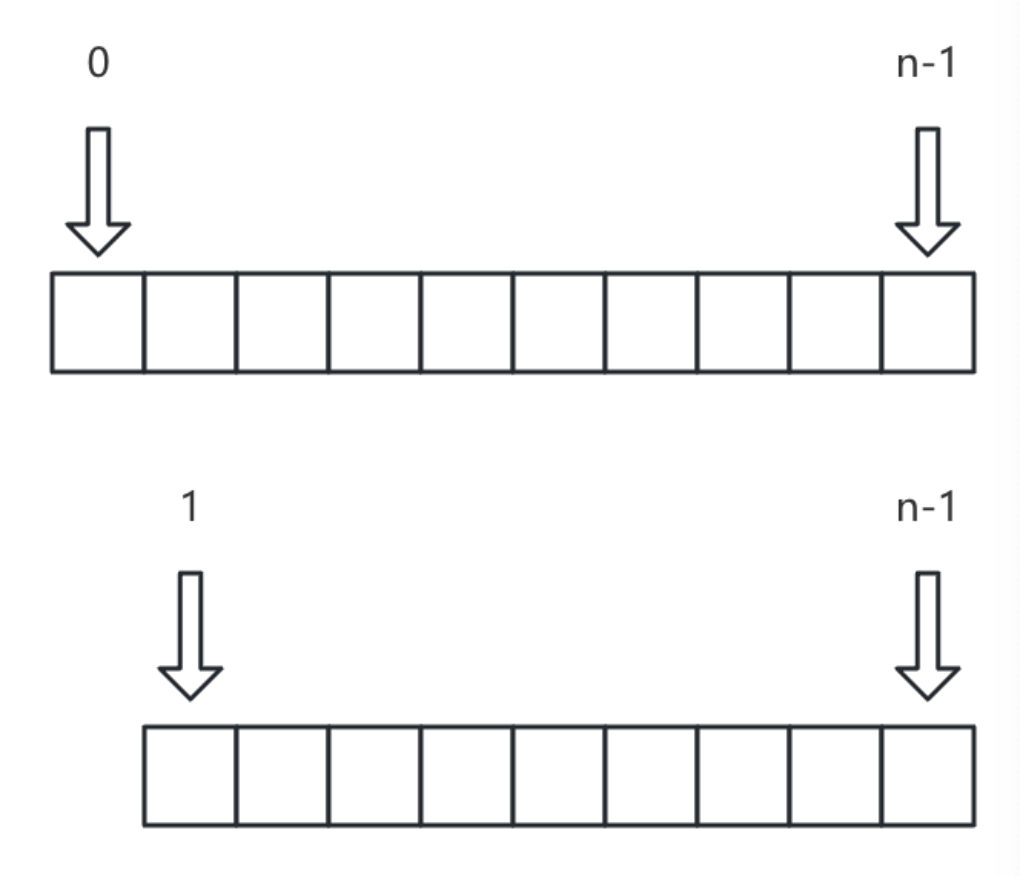
我们每次将当前数组的中间位置元素与待查找元素比较,中间元素小,那就查找右侧子数组,反之查找左侧
每次查找都要“砍去”一半数组,数一数一共砍了几次即可得到时间复杂度O(logN)
3.1.局部最小
无序也可以用二分
长度为N的数组,规定相邻位置的元素一定不相等,如果0位置的数比1位置的数小,那么0位置的数是局部最小;如果N-1位置的数比N-2位置的数小,那么N-1位置的数为局部最小;对于中间位置i,如果i位置的数不仅比i-1位置的数小,而且比i+1位置的数小,那么i位置的数为局部最小。易得该数组必定存在至少一个局部最小
(1) 先看0位置的数是否小于1位置的数,若小则直接返回
(2) 看N-1位置的数是否小于N-2位置的数,若小则直接返回
(3) 我们取中点位置M,若[M] > [M-1],则向左侧子数组查找;若[M] < [M-1]且[M] > [M+1],则向右侧子数组查找;若都不满足,则[M]为局部最小
4.递归
一道题引入递归
问:
找到一个数组的最大值
答:
不断把当前数组拆成两个子数组,返回两个子数组的最大值中较大的那个
public static int getMax(int[] arr) {
return process(arr, 0, arr.length-1);
}
public static int process(int[] arr, int L, int R) {
if (L == R) {
return arr[L];
}
int mid = L + ((R - l) >> 1);
int leftMax = process(arr, L, mid);
int rightMax = process(arr, mid+1, R);
return Math.max(leftMax, rightMax);
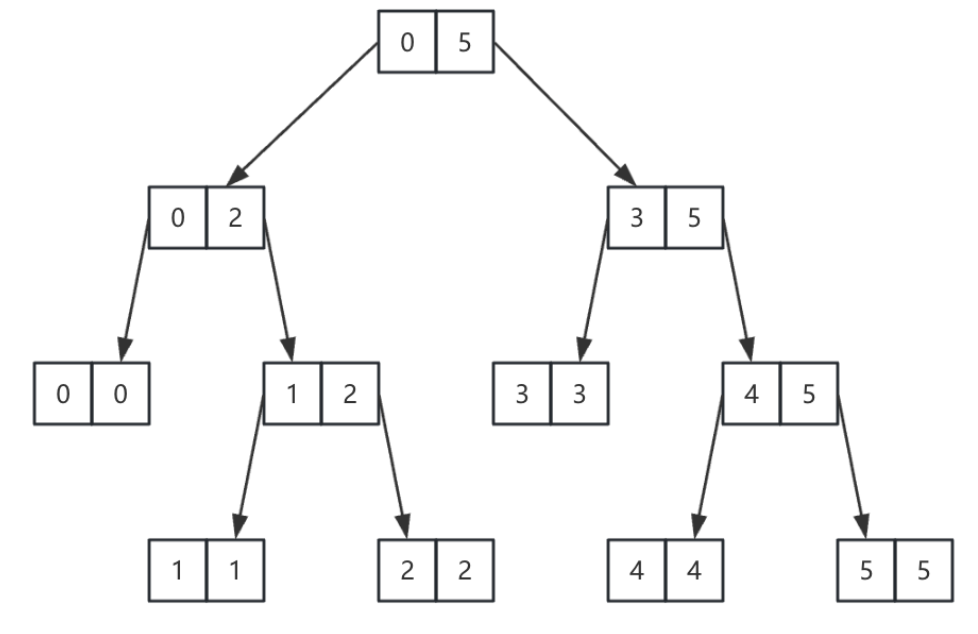
}对该数组进行递归
画出它的递归结构图
把递归的过程理解为一棵多叉树,每一个节点都通过子节点为自己汇总信息之后才能继续往上返回,栈空间就是整棵树的高度
4.1.递归行为时间复杂度的估计
- master公式
满足子问题等规模的递归都可以用master公式求时间复杂度
T(N) = a*T(N/b) + O(N^d)
T(N)指的是母问题的数据量是N级别的
T(N/b)指的是子问题的规模都是N/b
a指的是子问题的调用次数
O(N^d)指的是除了调用子问题之外,剩下过程的时间复杂度
值得注意的是a/b未必等于1,因为以下式子同样满足master公式
T(N) = 2T(2N/3) + O(1)
结论:
logba < d ====> O(N^d)
logba > d ====> O(N^(logba))
logba == d ====> O((N^d)*logN)