Time is free, but it's priceless. You can't own it, but you can use it.
承接上文建模步骤,现在就来正式讨论一个时间序列模型的例子,以下为原数据集和测试集格式
链接:https://pan.baidu.com/s/1wR7-w3vGKv03FzQPR3KqhA?pwd=Data
提取码:Data
数据观察
对初始数据的观察,是所有模型的基础,没有对自己将要处理的数据有基础的认知,是没有办法做好特征工程的,于是乎,我们使用matplotlib进行趋势观察,横轴为时间,纵轴为销售额
我们很明显的发现,在一周内的预测值都有相同的趋势,猛的升上去,经过几天的波动,再大幅的下跌,而且每一个七天都有着这样的走势,所以提醒一下自己可以通过分解时间序列模型得到时变特征——趋势与季节性
同时我们发现一个特殊点:国庆!!!
国庆的数据会大幅度下跌,形成和原来完全不一样的情况,所以我们可以通过增加特征额外标记出国庆,让模型知道国庆值是非常特殊的
数据预处理
数据预处理包括数据清洗,由于老师手下留情所以本测试集不包含NaN,可以放心食用
数据预处理第二步,加上我们的测试集。加上测试集的理由:提取特征时不仅要将训练集的特征提取,还需要提取测试集的特征用于预测,为了避免重复的特征提取操作,所以需要将测试集与原训练集连在一起(当然此时测试集的销售额当然是NaN,但这是无法避免的)
数据预处理第三步,由于原来的数据集是一个宽表(所有的值横向排列),但是我们的时间序列模型大部分都需要转换为长表,将时间放到index列,才是时间序列模型习惯的做法。并且将整个值全部展开成一列(意思是整个长表最后只有三列,一列id,一列时间,一列sales)并进行sortvalues(),这样能够帮我们更好的分类数据,赋值数据,更好的处理特征
# 导入csv作为DataFrame
train = pd.read_csv('train.csv')
submission = pd.read_csv('submission_3days.csv')
last_day = train.iloc[:, [-1]].columns.to_list()[0] # 逐行解析,iloc是根据数值获取对应列,
# 上面有一个重点,就是iloc[:, -1]只能够选取到pd.Series,是没有columns的,按照[:, [-1]]的写法就是pd.Dataframe,才有columns也就是标签这个属性
# tolist就是转换为列表,因为获取到的columns本质上是一个属性,是列标签,所以通过tolist转换为列表才能获得对应的时间值,最后取唯一的元素
last_day = datetime.strptime(last_day, '%Y-%m-%d %H:%M:%S') + timedelta(days=1) # 本质上为datatime时间的初始化
# 上面表述的是最后一天时间格式从str -> datatime格式,并且最后一天的基础上加上了一天,原因与下面的data_range有关,要从预测的那天开始取
p_dates = pd.date_range(last_day, periods=P_HORIZON) # 从预测的那天开始,periods代表的是包含的时间数量,这里为预测的那三天
test = train[['id']].copy() # 将id这一列连同标签一起赋值,不会影响到train,复制出来只有id的一列
test[p_dates] = np.nan # 因为p_dates是一个列表,这里可以认为是dict添加元素的感觉,对这三天的所有id赋予NaN
# 拼接
dataset = pd.merge(train, test, on='id') # pandas的拼接操作,根据id,将预测的那三天放到最后
# 列转行,一定要按照['id','timestamp'],升序排列
df = dataset.copy() # 使用df
df = pd.melt(df, id_vars=['id', 'dep_id', 'commodity_mode_id'], var_name='timestamp', value_name='sales')
# melt函数将宽列表(原来157列)转换为长列表(现在12320行)
# id_var:不要转换的列;value_var:要转换的列(如果两个都不在就会丢失数据,所以如果id_var以外其他都要转,这里其中value_var就不填
# var_name:定义经过现在代表时间的列名字;value_name:定义展开后原来销售值的列名字
df['timestamp'] = pd.to_datetime(df['timestamp']) # 将这一列全部转换为datatime的标准形式
df.sort_values(by=['id', 'timestamp'], inplace=True) # 根据id先排列,再根据时间排序(这样保证所有时间都是顺序),inplace是替换的意思
grid_df = df[['id', 'timestamp', 'sales']].copy() # 取出没用的商店和商品id
# grid_df是处理好的列表,12320,3,代表不同uid的所有时间的sale接下来就是划分数据集,这部分还是很重要的,直接给出代码,因为不同要求能做很多种数据分割,使用函数,自己定义,都是很好的方法
能正确运行出来的代码都是好代码
FIRST_DAY = '2018-06-01' # 第一天,因为滚动窗口或者滞后项会导致一开始的数据缺失,所以将开始日期设置到6.1是偏保险的决定,PS!!!!!!!!!建议debug看存在缺失值的日期后再次决定开始日
validations = {
'cv4': ['2018-10-13', '2018-10-17'], # cv是交叉验证的意思(个人看法),这里预测5天,test为5
'test': ['2018-10-18', '2018-10-22']
}
cvs = ['cv4']
for cv in cvs: # grid_df是特征列表,大家根据自己特征列表的名字替换也行,这里给出的是思路以及一些注意事项
print(f'cv: {validations[cv]}, target: {TARGET}')
tr_mask = (grid_df['timestamp'] < validations[cv][0]) & (grid_df['timestamp'] >= FIRST_DAY)
# tr_mask = FIRST_DAY <= grid_df['timestamp'] < validations[cv][0]
# 要求时间< cv第0天,以及大于第一天,不可改为上面,原因如下,就像不能用and一样
# 作为dataframe的切片一定得用&不能用and,不然会报错的,这里叫train_mask,下面是value_mask
vl_mask = (grid_df['timestamp'] >= validations[cv][0]) & (grid_df['timestamp'] <= validations[cv][1])
X_train = grid_df[tr_mask][feats] # 这里截取所有训练集里的全部特征
Y_train = grid_df[tr_mask][TARGET] # 这里截取所有训练集里的全部值
X_val = grid_df[vl_mask][feats] # 这个就是验证集力,特征
Y_val = grid_df[vl_mask][TARGET] # 验证集的值
# 取出测试集特征
cv = 'test'
pred_mask = (grid_df['timestamp'] >= validations[cv][0]) & (grid_df['timestamp'] <= validations[cv][1])
# 让时间在训练集里,取出值
X_pred = grid_df[pred_mask][feats] # 根据特征特征工程
先进行时间戳特征的提取啦
A:时间戳特征
时间序列模型最基本的特征,所有时间序列都具有的特征,根据时间标准的不同(如有些股票数据精确到秒)可以分为年,月,日,星期,时,分,秒,是否月末月初节假日等特征,这些可以根据需要选取(无用特征反而会损失模型精度)
# 提取时间戳对象属性, 时变特征需要我们自己去找
temp_dt = grid_df['timestamp'].dt # 这个dt是高级接口,可以通过temp_dt获得所有的时间戳特征,不过它只是接口,无法print
# 以下为统一处理,这里和上面的为预测值创建NaN一样,是字典添加元素的想法
grid_df['month'] = temp_dt.month # 月, int
grid_df['day'] = temp_dt.day # 日, int
grid_df['dayofweek'] = temp_dt.dayofweek # 星期几, int
grid_df['is_month_start'] = temp_dt.is_month_start # 是否是本月第一天, bool
grid_df['is_month_end'] = temp_dt.is_month_end # 是否是本月最后一天, bool
grid_df["is_celebrate"] = np.where((grid_df["timestamp"] >= "2018-10-01") & (grid_df["timestamp"] <= "2018-10-07"), True, False)B:时变特征提取
1)滞后项
滞后项可以作为预测当天的一个重要特征,由于观察到固定时间频率为7天,所以我们可以将过去第七天的数据作为我们的模型判断依据(模型可以根据这个值大概估计今天的值,所以将这个作为特征)。
PS:这也意味着前七天的数据将缺乏滞后项,导致这个特征为NaN,我们最后在截取训练集的时候需要重视这一点!!!!!!!!!!!
2)滑动窗口
滑动窗口的实现主要通过rolling,pandas的dataframe已经内置好了完整的一套滑动窗口的实现,mean(), std(). min(), max(), sum()分别为平均值,标准差,最小值,最大值和平值。
PS:注意滑动窗口使用会导致边缘数据缺失!!!!
3)拓展窗口
拓展窗口的实现则是expending,同样内置了一整套与滑动窗口相对应的方法,与滑动窗口相同
这里给出时变特征的代码 (建议使用groupby,会方便很多),中间的注释行可以省略,是调用groupby的apply方法才需要使用
def time_change():
group = data.groupby("id")
#滞后项提取,根据id分组
data["shift"] = group["sales"].shift(7)
# 这里的内容是使用groupby中的apply才看的,主要是对实例方法进行形参的调用,使用transform则不需要
# def temp(group, func):
# """因为实例方法的原因,直接输入func会导致不使用这个形参
# 因此现在尝试使用getattr函数调用func
# 第一层apply(lambda x是group函数的,每个id下对sales的滚动(可以无视这一行)
# 第二层apply(lambda y是对每一个rolling进行func操作
# 最后reset_index脱离group重回dataframe"""
# return group["sales"].shift().rolling(7).apply(lambda y: getattr(y, func)())
# 为了避免自己的时间数据泄露,需要先shift从昨天开始,在进行滚动窗口
data["window_mean"] = group["weekday"].transform(lambda x: x.shift().rolling(7).sum())
data["window_std"] = group["sales"].transform(lambda x: x.shift().rolling(7).std())
data["window_max"] = group["sales"].transform(lambda x: x.shift().rolling(7).max())
data["window_min"] = group["sales"].transform(lambda x: x.shift().rolling(7).min())
# 这里是对所有时间序列进行拓展窗口,如果想要让模型更精确一点,可以考虑我们之前观察到的7天周期,做对应星期几的拓展窗口,例如星期三就取过去星期三的拓展窗口
# group = data.groupby(["id", "dayofweek"]) # 这里默认就是再按照星期几来拓展,想用就取消注释,但是注意,这里的expanding就要取1,因为此时一个数据间隔代表了原来7天的一个周期
data["history_mean"] = group["sales"].transform(lambda x: x.shift().expanding(7).mean()) # 使用星期分类记得将7改成1
data["history_std"] = group["sales"].transform(lambda x: x.shift().expanding(7).std())
data["history_max"] = group["sales"].transform(lambda x: x.shift().expanding(7).max())
data["history_min"] = group["sales"].transform(lambda x: x.shift().expanding(7).min())重点来力!!!!!!!!!!!!
获取趋势和滞后项的时变特征
1)刚开始为了严谨,我们采用傅里叶变换进行周期提取(由于实战化教程这里仅进行如何使用以及使用的注意事项)
傅里叶变换进行周期提取,这里给出代码实例
def fftran(series):
series = np.diff(series["sales"].values, 0).tolist() # 差分处理,如果需要差分调整其中的0
adf = sm.tsa.adfuller(series) # 检验序列平稳性,要想更好的提取出周期,需要协方差平稳
p = adf[1]
diff_time = 0 # 差分次数
while p > 0.05: # p越小越能拒绝原序列不平稳的原假设
series = np.diff(np.log(series), 1)
adf = sm.tsa.adfuller(series)
p = adf[1]
diff_time += 1 # 我们默认进行一阶差分,如果使用季节性差分则使用周期次差分
length = len(series)
fft_y = np.abs(np.array(sp.fftpack.fft(series))) # 进行傅里叶变换得到y值,注意fft变换关于x轴对称(在频率轴的两侧镜像对称,为了方便提取这里采用abs)
fft_y = fft_y / length # 将值归一化
fft_y = fft_y[:length // 2] # 由于傅里叶变换有对称性(不是上面的关于频率轴的对称),所以我们只需要取一半的取值,进行周期的提取
fft_x = range(length // 2) # 作为频率轴
max_x = sp.signal.argrelextrema(fft_y, np.greater) # 这是scipy的获取极大值点的函数,傅里叶变换中,极大值点的频率值代表了一个频率
max_y = fft_y[max_x] # 取出极大值点的频率
f_max_sort = np.argsort(f_max) # 获得极大值的索引排序,numpy的argsort是最大值排序的索引
ref = np.array([max_loc[0][i] for i in list(reversed(f_max_sort))]) # 对应到极大值索引排序,也就是频率
period_notdeal = length / ref + diff_time # 周期 = 总长 / 频率 + 差分次数
period = np.around(period_notdeal).tolist() # 因为总长 / 频率可能会小数,这里的周期是day,只能是整数,所以进行四舍五入
len_period = len(period)
total = []
for i in period: # 取出每一个周期进行自回归系数acf
acf = sm.tsa.acf(series, nlags=i)[-1] # 取出acf得分,nlags你可以想成周期
total.append(acf) # 将所有周期的acf的得分加入total中
result = sorted([(period[i], total[i], period_notdeal[i]) for i in range(len_period)], key=lambda x: x[1], reverse=True) # 根据得分排序
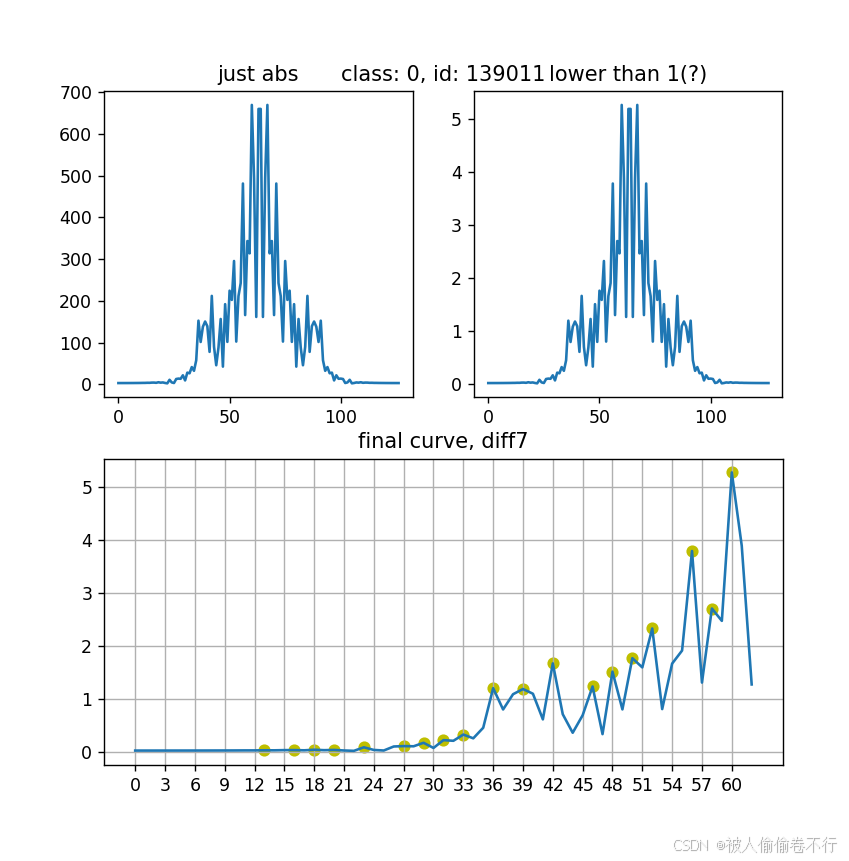
return result[0] # 返回得分最高的值作为周期做了几张其他id的图表(得出有时候经验判断大于模型计算),有些序列无论经过几阶差分,这里的周期都难以判断,当然也有些能很明显的提取出两个周期(如第二张图)
所以最终,还是以经验判断周期固定取7才是最好的呐
2)时间序列分解:
我尝试过的时间序列分解有两种,一种是STL分解,一种是seasonal_decompsed分解,都可以使用statsmodel.api调用
STL适合噪音比较强的模型,seasonal_decomposed需要序列平稳才能比较好分解(而国庆的数据摆在那里就注定了异常值的存在)
所以最后这里我们还是采用STL进行模型分解
group = data.groupby("id")
def STL(group):
new_group = group[["sales", "time"]].iloc[:151] # 取出有用的部分
# new_group["sales"] = new_group["sales"].apply(lambda x: np.log(x)) # 是否先取对数平滑(减小差分)
new_group.set_index("time", inplace=True) # 将时间作为索引
model_stl = sm.tsa.STL(new_group, period=7).fit() # 建立时间序列分解模型
return model_stl
stl_group = group.apply(STL, include_groups=False) # 这里所有的返回值是pd.Series,values是model,方便我们提取季节项和趋势
trend_group = pd.DataFrame(stl_group.reset_index()) # 返回df对象好操作,并且根据80个id分解的是80个模型
trend_group.columns = ["id", "trend"]
data["trend"] = stl_group.apply(lambda x: x["trend"].trend).explode("trend").values # 记住,一开始获得的是80个列表的df,我们需要将其explode展开取值,才能重新赋值给data
seasonal_group = pd.DataFrame(stl.group.reset_index())
seasonal_group.columns = ["id", "seasonal"]
data["seasonal"] = stl_group.apply(lambda x: x["seasonal"].seasonal).explode("seasonal").values
# 这里和上面趋势分解的步骤一样,这里有更优化的写法,但是之前想到这个就这样写了
# 反正本地部署的时候代码能正确跑出结果就行(
# 这里只是提供思想,请根据需要(也可以结合ai)将代码调教成自己模型的形状就行模型建立:
A)简单线性回归
由于线性回归特殊性,所有变量都需要转换为哑变量,所以这里仅能使用时间戳特征进行线性回归(当然实际建模的时候基本上不用这个模型,所以是建模过程展示以及验证方式确认)
def reg_metrics(y_true, y_pred):
y_true = np.nan_to_num(y_true) # 取出缺失值用0替代
y_pred = np.nan_to_num(y_pred)
mae = mean_absolute_error(y_true, y_pred) # mae平均绝对误差
mse = mean_squared_error(y_true, y_pred) # mse均方误差
rmse = np.sqrt(mse) # 均方根误差
return {'mae':mae, 'mse':mse, 'rmse':rmse} # 误差展示
reg = LinearRegression() # 正常回归模型实例化
reg.fit(X_train, Y_train) # 进行训练,这里训练是超级多个01变量拟合的一个线性回归模型
pred_val = reg.predict(X_val) # 进行预测
res = reg_metrics(Y_val, pred_val) # 这里为进行检验,可以省略
print(res)
B)层次聚类
层次聚类可以将时间序列进行分类,将销售热度近似的id进行汇总,并分别建立不同模型(一般聚完类会重新回到数据观察,建立不同的特征),以此提高拟合精度。(如果有兴趣的话可以尝试着做更好的层次聚类,因为时间精力有限加上本人不太会用聚类,所以这里仅给出示例代码帮助大家运用到自己的模型中)
fig = plt.figure(figsize=(25, 7)) # 建立画布
sub1 = fig.add_subplot(121) # 设置sub
sub2 = fig.add_subplot(122)
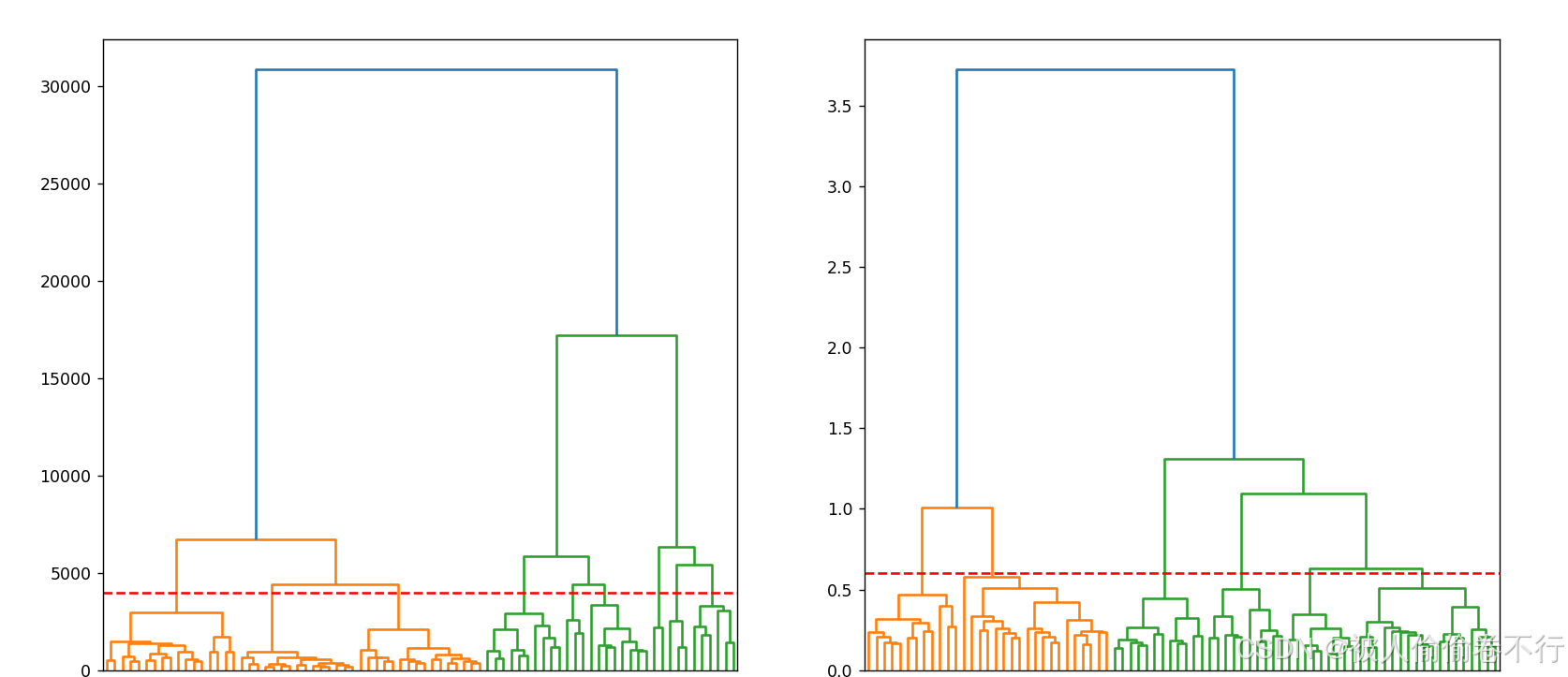
dendrogram(linkage(temp, method='ward'), ax=sub1) # 画进sub1中
sub1.axhline(y=4000, color='r', linestyle='--') # 画分界线帮助我们分析要聚多少类
dendrogram(linkage(normalize_temp, method="ward"), ax=sub2) # 同上理,其不同在于上面不进行标准化
sub2.axhline(y=0.6, color='r', linestyle='--')
plt.show()
cluster = AgglomerativeClustering(n_clusters=6, metric='euclidean', linkage='ward') # 使用sklearn中的层次聚类,可以直接聚出id所属类别
cluster.fit_predict(normalize_temp)
print(cluster.labels_.tolist()) # 最后的结果其实蛮理想的,将80个id全部聚好了类,一共6类[3, 4, 1, 4, 3, 0, 5, 0, 2, 0, 1, 4, 5, 0, 1, 4, 2, 0, 1, 4, 5, 0, 5, 4, 2, 2, 0, 1, 0, 2, 0, 5, 1, 4, 1, 0, 5, 0, 3, 1, 4, 2, 0, 1, 5, 0, 1, 4, 2, 0, 2, 0, 3, 0, 1, 1, 4, 1, 4, 5, 0, 3, 4, 2, 3, 3, 3, 2, 1, 3, 0, 1, 5, 1, 2, 0, 3, 1, 1, 2]
C)压轴出场的👑来辣——XGBoost
xgboost也能够进行线性模型,但是效果没有树模型好,所以xgboost一般就是树模型在用
建模的过程并不复杂,并且在之前的文章也有引用过,将特征填进去就万事大吉
# 这个是参数列表,用于求出最优解
param_grid = {
"learning_rate": [0.01, 0.1, 0.2, 0.05], # 学习率
"max_depth": [3, 5, 7], # 树深度
"subsample": [0.8, 0.9, 1.0] # 样本采样率
}
# 网格搜索交叉验证,模型,参数
grid_search = GridSearchCV(XGBRegressor(), param_grid, cv=3)
grid_search.fit(X_train.drop("id", axis=1), Y_train) # 模型拟合
best_params = grid_search.best_params_ # 提取最优参数
xgb_model = XGBRegressor(**best_params) # 模型实例化
xgb_model.fit(X_train.drop("id", axis=1), Y_train) # 建立模型
predictions = xgb_model.predict(X_val.drop("id", axis=1)) # 预测,但是这里的值不准
rmse = np.sqrt(mean_squared_error(Y_val, predictions))
print(rmse)
plot_importance(xgb_model) # 可以获得所有特征的重要性
plt.show()预测
The real challenge lies ahead.
当我们预测时发现,时变特征的缺失(最后两天都无法使用滚动窗口的特征),导致我们在进行时间预测的时候无法一次性预测,所以只能逐步预测(要是有别的方法也可以评论出来告诉我),缺点是误差的累计,越预测越不精确
一共预测三天,那么需要分天预测,预测完将sales重新赋值回去,每预测一天就需要重新进行时变特征的计算,于是乎,time_change作为方法就可以直接调用,这部分时变特征也解决了
但是!!趋势和季节性这部分的时变特征还没有解决
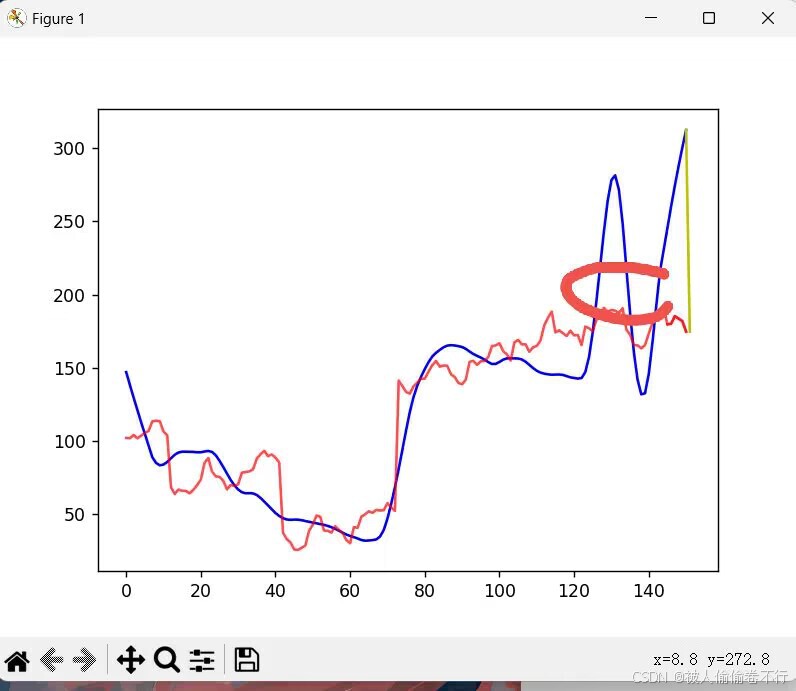
最痛苦且无法解决的事,同时将前面的伏笔国庆节展现出来的,那就是趋势和季节性的使用
因为国庆节整个趋势的大幅下降,让线性回归预测趋势的模型误认为十月份就是下降的趋势,所以在预测上便会偏低很多,即使通过标注data.loc[(data["time"] >= "2018-10-01") & (data["time"] <= "2018-10-07"), "holiday"],也无法解决整体趋势下降的问题,这时候引入两种解决方法
趋势
(1)magic number
在实际工作中,节假日本身就会导致模型预测的异常,这时候magic number就发挥其作用,我们可以对实际的预测值 × 2倍,或者将过去三天进行预测,与实际值进行相除(过去三天实际 / 过去三天预测)取出最大倍数并作为magic number
(2)数据填充
因为我们并不预测节假日,所以我们可以将节假日与节假日调休变成普通的日子的销售额(请注意调休 !!!)
于是我们采用数据填充将节假日的影响冲淡
取过去2周(或者一个月)的同星期几的数据平均值作为填充(例如周三就选上周三和上上周三的数据平均值进行填充),类似于滚动窗口的思想,将过去两周的平均值作为自己数据的依据
然后再进行趋势预测或者使用magic number
季节性
季节性处理好办一些,毕竟规定了周期为7,所以此时只需要将季节性数据取shift(7)即可
最后附上这部分线性回归与季节性赋值代码
趋势线性处理方法
def linear_pre_trend(input_trend, id):
standard = MinMaxScaler() # 最大最小归一化
input_trend = input_trend.trend.values.reshape(-1, 1) # 获取trend并将其转换为二维列表,归一化模型传参需要
input_trend = standard.fit_transform(input_trend).flatten() # 获取归一化后数据,这种也算是归一化模板,可以记下来,最后使用flatten展开回一维列表
feat = data.loc[data["id"] == id, ["month", "day", "dayofweek", "holiday", "isweekend"]] # 截取想要的特征
feat[["month", "day", "dayofweek"]] = feat[["month", "day", "dayofweek"]].astype("category") # 标签化变量,用于哑变量处理中
feat = pd.get_dummies(feat)
feat_train = feat.iloc[:148 + day] # 所有训练集
cv_train = feat.iloc[148 + day: 151 + day] # 验证集三天
feat_test = feat.iloc[[151 + day]] # 预测一天,因为我们逐步预测所以一天一天预测
# model = LinearRegression() # 线性回归
# model.fit(feat_train, input_trend[:148 + day])
model = Lasso(alpha=0.00051) # 加上正则化系数r1的lasso回归
model.fit(feat_train, input_trend[:148 + day])
res = model.predict(feat_test) # 预测值
tt_res = model.predict(cv_train) # 验证集的值
yuan_res = input_trend[148 + day: 151 + day] # 预测集的真实值
cmp = np.max(np.divide(yuan_res, np.abs(tt_res))) # compare取得魔法数字
res = np.concatenate([input_trend, res * cmp]) # 将res与原趋势链接,获取预测到的趋势
res = np.pad(res, pad_width=(0, 154 - len(res)), constant_values=0) # 补上还没预测的天数的0
return pd.Series(res).values # 返回一个array,存放着这个id下的趋势季节性滞后处理方法
# 请注意,data里已有seasonal,是从上文STL分解后得到的seasonal,这里承接上文,如果要使用也请适配自己的模型
ttt = data.groupby("id")["seasonal"].transform(lambda x: x.shift(7).iloc[-3:]) # 根据id分组后取出季节性,并按照周期取上个周期的最后三天的季节性数据进行填充
data.loc[data["time"] >= "2018-10-18", "seasonal"] = ttt # 这里代表的是全体偏移值,应该要在groupby里面干
data["seasonal"] = data["seasonal"].astype("float")