一、并查集原理

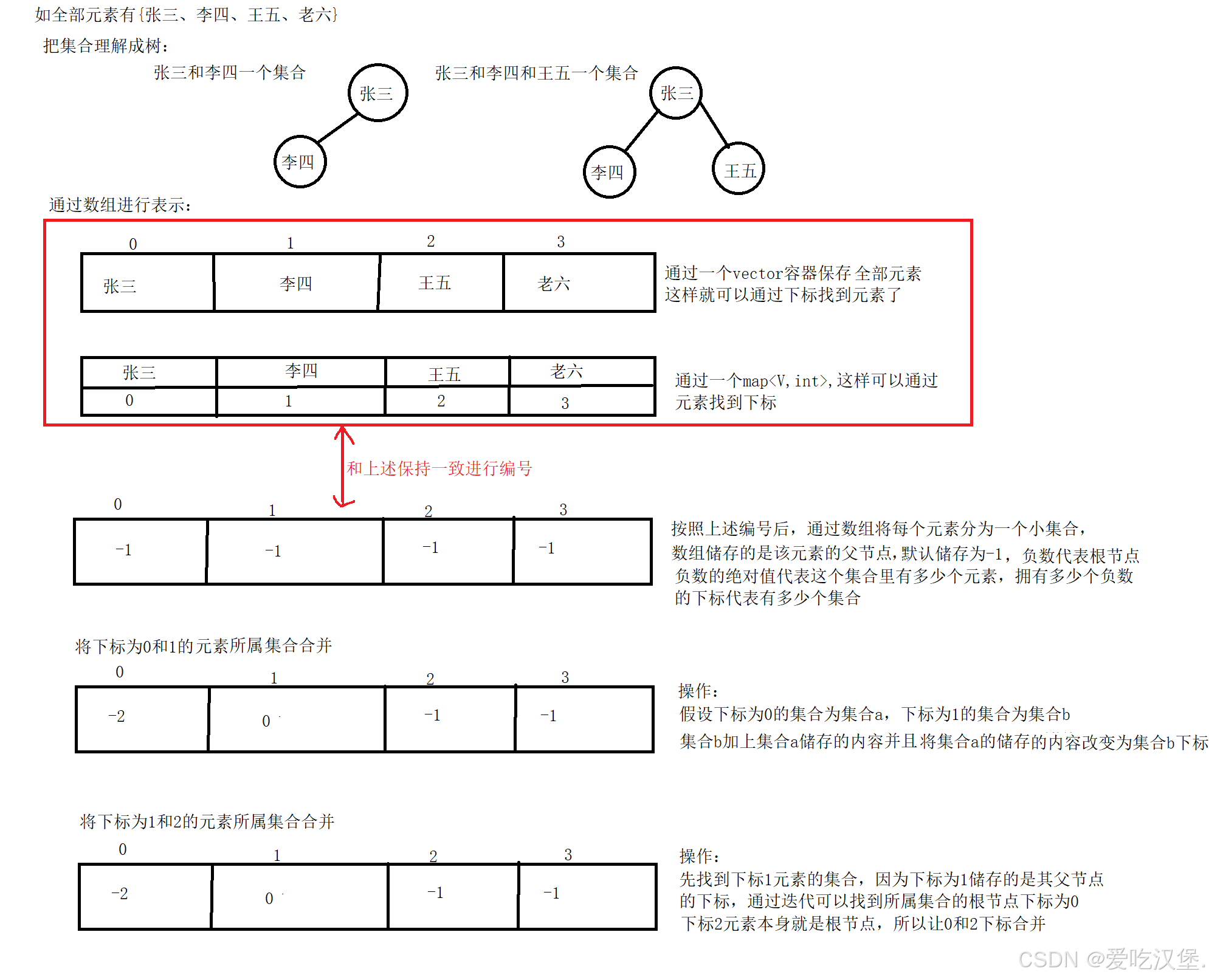
在一些应用问题中，需要将n个不同的元素划分成一些不相交的集合。开始时，每个元素自成一个单元素集合，然后按一定的规律将归于同一组元素的集合合并。在此过程中要反复用到查询某一个元素归属于那个集合的运算。适合于描述这类问题的抽象数据类型称为并查集(union-find set)。

二、并查集实现

常用操作：

1. 查找元素属于哪个集合 沿着数组表示树形关系以上一直找到根(即：树中中元素为负数的位置)
2. 查看两个元素是否属于同一个集合 沿着数组表示的树形关系往上一直找到树的根，如果根相同表明在同一个集合，否则不在
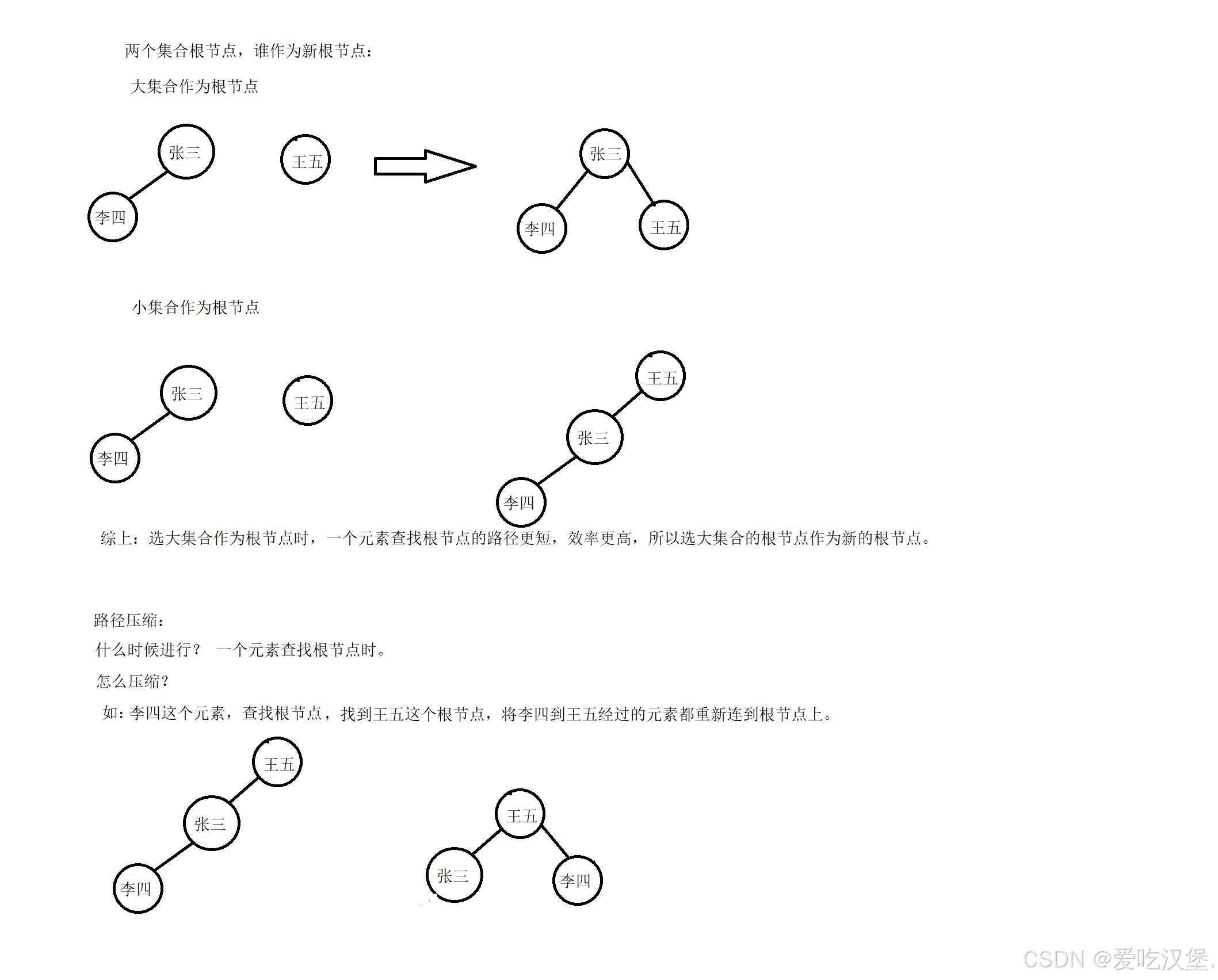
3. 将两个集合归并成一个集合 将两个集合中的元素合并 将一个集合名称改成另一个集合的名称
4. 集合的个数 遍历数组，数组中元素为负数的个数即为集合的个数。

实现：

#include<iostream>
#include<vector>
#include<map>

using namespace std;

template<class V>
class UnionFindSet
{
public:
	//初始化
	UnionFindSet(const vector<V> & element)
	{
		int n = element.size();

		//初始化集合
		_ufs.resize(n, -1);

		//初始化映射关系
		_element.resize(n);
		for (int i = 0; i < n; i++)
		{
			_element[i] = element[i];
			_indexmap[element[i]] = i;
		}
	}

	//获取下标
	int GetIndex(const V& v)
	{
		//通过映射获取
		if (_indexmap.find(v) != _indexmap.end())
			return _indexmap[v];

		return -1;
	}

	// 给一个元素的编号，找到该元素所在集合的名称
	int FindRoot(int index)
	{
		//父下标为负数代表是该集合的根节点
		int root = index;
		while (_ufs[root] >= 0)
		{
			//迭代
			root = _ufs[root];
		}
		
		//路径压缩 -- 将index -> 根上的点都连接到根节点上
		while(_ufs[index] > 0)
		{
			int p = _ufs[index];
			_ufs[index] = root;		//改变父下标
			index = p;
		}
		return root;
	}
	
	//将两个元素合拼到同一个集合里
	bool Union(V v1, V v2)
	{
		//获取下标
		int x1 = GetIndex(v1);
		int x2 = GetIndex(v2);

		//获取两个元素的根节点下标
		int root1 = FindRoot(x1);
		int root2 = FindRoot(x2);
		if (root1 == root2)
			return false;

		//小的并到大的里面 -- 减少路径长度
		if(abs(_ufs[root1]) < abs(_ufs[root2]))
			swap(root1,root2);

		//连接
		_ufs[root1] += _ufs[root2];	//每一个元素的下标初始为-1，根节点下标的绝对值代表这个集合元素个数
		_ufs[root2] = root1;

		return true;
	}

	// 数组中负数的个数，即为集合的个数
	size_t Count()const
	{
		//遍历+统计
		size_t ret = 0;
		for (int i = 0; i < _ufs.size(); i++)
		{
			if (_ufs[i] < 0)
				ret++;
		}

		return ret;
	}

private:
	map<V, int> _indexmap;	//通过元素找到映射的下标
	vector<V> _element;		//通过下标找到映射的元素
	vector<int> _ufs;		//集合
};

三、并查集的应用

使用并查集解决下面题目：
题目：省份数量

使用算法：并查集
将相连的城市放到一个集合里，最后统计集合的个数即可。

代码：

并查集代码
//
class Solution {
public:
    int findCircleNum(vector<vector<int>>& isConnected) 
    {
    	//创建集合
    	vector<int> v;
    	for(int i = 0; i < n; i++)
    		v.push_back(i);
        UnionFindSet<int> ufs(v);
		
		//遍历二维数组
         for(int i = 0; i < isConnected.size(); i++)
         {
            for(int j = 0; j < isConnected[i].size(); j++)
            {
            	//相连进入一个集合
                if(isConnected[i][j] == 1)
                {
                    ufs.Union(i,j);
                }
            }
         }
		
		//返回集合数量
         return ufs.Count();
    }
};

但是在实际写题中手写一个并查集很浪费时间，所以一般提取核心思想部分融入我们的代码中，如使用一个数组模拟。

class Solution {
public:
    int findCircleNum(vector<vector<int>>& isConnected) 
    {	
        int n = isConnected.size();
        //模拟并查集
        vector<int> _ufs(n,-1);

        // 给一个元素的编号，找到该元素所在集合的名称
        auto FindRoot = [&_ufs](int index)
        {
            int n = index;
	        while (_ufs[n] >= 0)
	        {
		        n = _ufs[n];
	        }
            return n;
        };

        for(int i = 0; i < n; i++)
        {
            for(int j = 0; j < isConnected[i].size(); j++)
            {
                //i j 相连
                if(isConnected[i][j] == 1)
                {
                    //查找i,j集合的根节点下标
                    int root1 = FindRoot(i);
		            int root2 = FindRoot(j);

                    //不在一个集合，进行合并
                    if(root1 != root2)
                    {
                        _ufs[root1] += _ufs[root2];
		                _ufs[root2] = root1;  
                    }
                }
            }
        }

        //遍历，负数说明是一个集合的
        int ret = 0;
        for(int i = 0; i < n; i++)
        {
            if(_ufs[i] < 0)
                ret++;
        }

        return ret;
    }
};