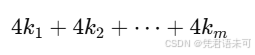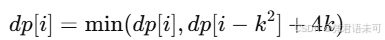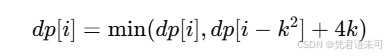问题描述

思路分析

这道题可以抽象为一个最优化问题：

问题分析

• 每个正方形的面积为 k² ，对应的边长为 k ，周长为 4k 。
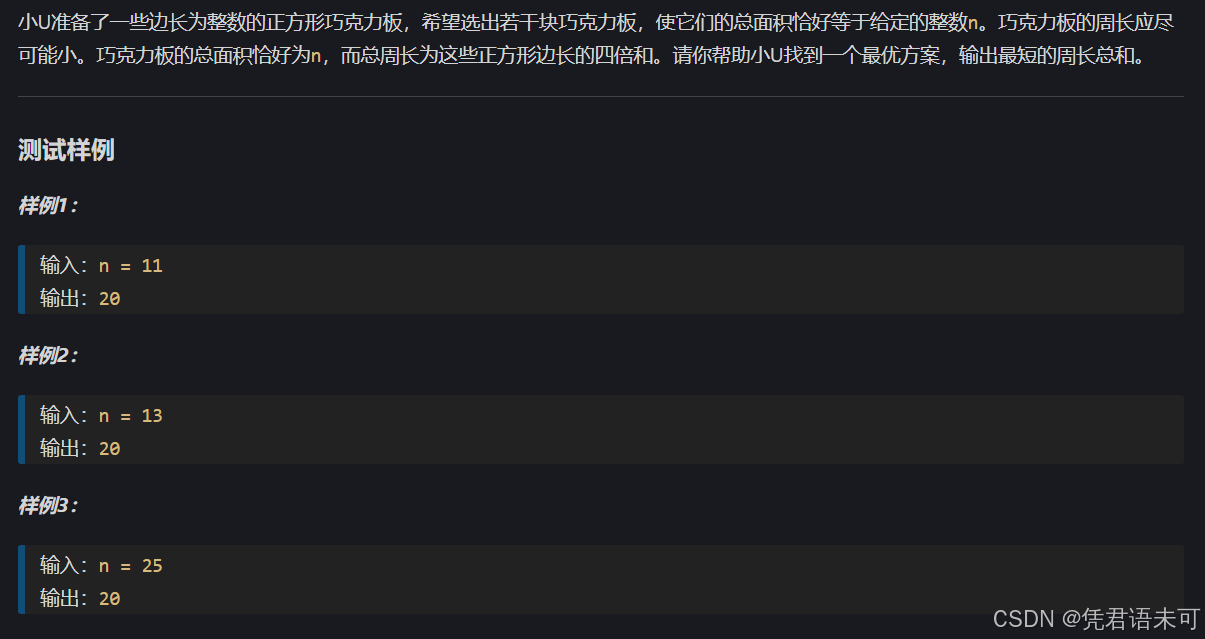
• 给定整数 n ，我们需要找到若干正方形，使得它们的面积之和恰好等于 n：
  
  同时尽量最小化这些正方形的周长总和：
  

​

解题方法

为了找到最优解，我们可以使用动态规划。

1. 动态规划的定义

用 dp[i] 表示面积为 i 时的最小周长。
最终答案即为 dp[n] 。

2. 状态转移方程

对于任意 i ，尝试使用边长为 k 的正方形：

• 面积为 i 时，如果选择一个边长为 k 的正方形，其面积是 k² ，对应周长为 4k 。
• 转移方程为：
  
  其中 k 是满足 k² ≤ i 的所有正方形边长。

3. 初始条件

• dp[0]=0：面积为 0 时，总周长为 0 。
• 对于 i > 0，初始值设置为无穷大（表示尚未计算）。

4. 求解顺序

从小到大遍历面积 i ，对每个 i 再遍历所有可能的 k ，逐步计算出最优解。

参考代码（Java）

import java.util.Arrays;

public class Main {
    public static int solution(int n) {
        // 动态规划数组，存储面积为 i 时的最小周长
        int[] dp = new int[n + 1];
        Arrays.fill(dp, Integer.MAX_VALUE); // 初始化为最大值
        dp[0] = 0; // 面积为 0 时周长为 0

        // 遍历每个面积
        for (int i = 1; i <= n; i++) {
            // 遍历所有可能的正方形边长 k
            for (int k = 1; k * k <= i; k++) {
                dp[i] = Math.min(dp[i], dp[i - k * k] + 4 * k);
            }
        }

        return dp[n];
    }

    public static void main(String[] args) {
        System.out.println(solution(11) == 20); 
        System.out.println(solution(13) == 20); 
        System.out.println(solution(25) == 20); 
    }
}

代码分析

1. 初始化部分

int[] dp = new int[n + 1];
Arrays.fill(dp, Integer.MAX_VALUE); // 初始化为最大值
dp[0] = 0; // 面积为 0 时周长为 0

• dp[i] 的含义：
  dp[i] 表示当总面积为 ( i ) 时，最小的周长和。

• 初始化逻辑：

  • 将所有 dp[i] 初始化为一个大值（Integer.MAX_VALUE），表示尚未计算过或者无效状态。
  • 特殊情况：dp[0] = 0，表示面积为 0 时，周长为 0（无需使用任何正方形）。

2. 外层循环：遍历面积

for (int i = 1; i <= n; i++) {

• 目的：
  从面积 1 到 n ，依次计算每个面积的最小周长。

3. 内层循环：尝试不同正方形

for (int k = 1; k * k <= i; k++) {
    dp[i] = Math.min(dp[i], dp[i - k * k] + 4 * k);
}

• 逻辑：

  • k 是正方形的边长。
  • k² 是正方形的面积。
  • 4k 是正方形的周长。

• 核心转移：
  对于当前面积 i ，尝试所有可能的正方形面积 k² ，更新最优解：
  

  • dp[i - k²] 表示面积减去 k² 后的最优周长。
  • + 4k 是新增正方形的周长。

• 条件 k * k <= i：
  仅考虑 ( k ) 的平方不超过当前面积 ( i )，否则超出范围。

4. 返回结果

return dp[n];

• 最终，返回 dp[n]，即面积为 n 的最小周长和。

复杂度分析

时间复杂度

• 总时间复杂度为：O(n√n)

空间复杂度

• 仅使用一个大小为 n+1 的数组 dp，空间复杂度为 O(n) 。