约瑟夫问题
约瑟夫问题的起源可以追溯到犹太历史学家弗拉维奥·约瑟夫斯(Flavius Josephus)的自传。据他描述,在罗马人占领耶路撒冷时,他和40名犹太士兵被困在一个洞穴中。为了避免被罗马人俘虏,他们决定以抽签的方式自杀,每数到第3个人就自杀,直到剩下最后一个人。约瑟夫斯声称,他通过计算找到了一个位置,使得自己成为最后的幸存者。
这样的问题推广到数学问题即:
题目:
编号为 1 到 n 的 n 个人围成一圈, 从编号为 1 的人开始报数,报道 m 的人离开,下一个人继续从 1 开始报数, n - 1 轮结束以后,只剩下一个人,问最后留下的者的这个人编号是什么?
这个题目涉及到环形链表的概念。
想要解这道题,我们先看看什么是环形链表
头节点与尾节点首尾相接,变成了环形链表
用编程语言如何创建呢?
//创建结构体,节点
struct ListNode {
int val;
struct ListNode* next;
};
typedef struct ListNode ListNode;
//创建节点函数
ListNode* BuyNode(int x)
{
ListNode* node = (ListNode*)malloc(sizeof(ListNode));
if (node == NULL)
{
exit(1);
}
node->val = x;
node->next = NULL;
return node;
}
//创建环形链表
ListNode* createCircle(int n)
{
ListNode* phead = BuyNode(1);
ListNode* ptail = phead;
for (int i = 2; i <= n; i++)
{
ptail->next = BuyNode(i);
ptail = ptail->next;
}
//首尾相接
ptail->next = phead;
return ptail;
}
我们在创建环形链表函数的返回值不是 phead 而是 ptail,这点我们放在后面讲。
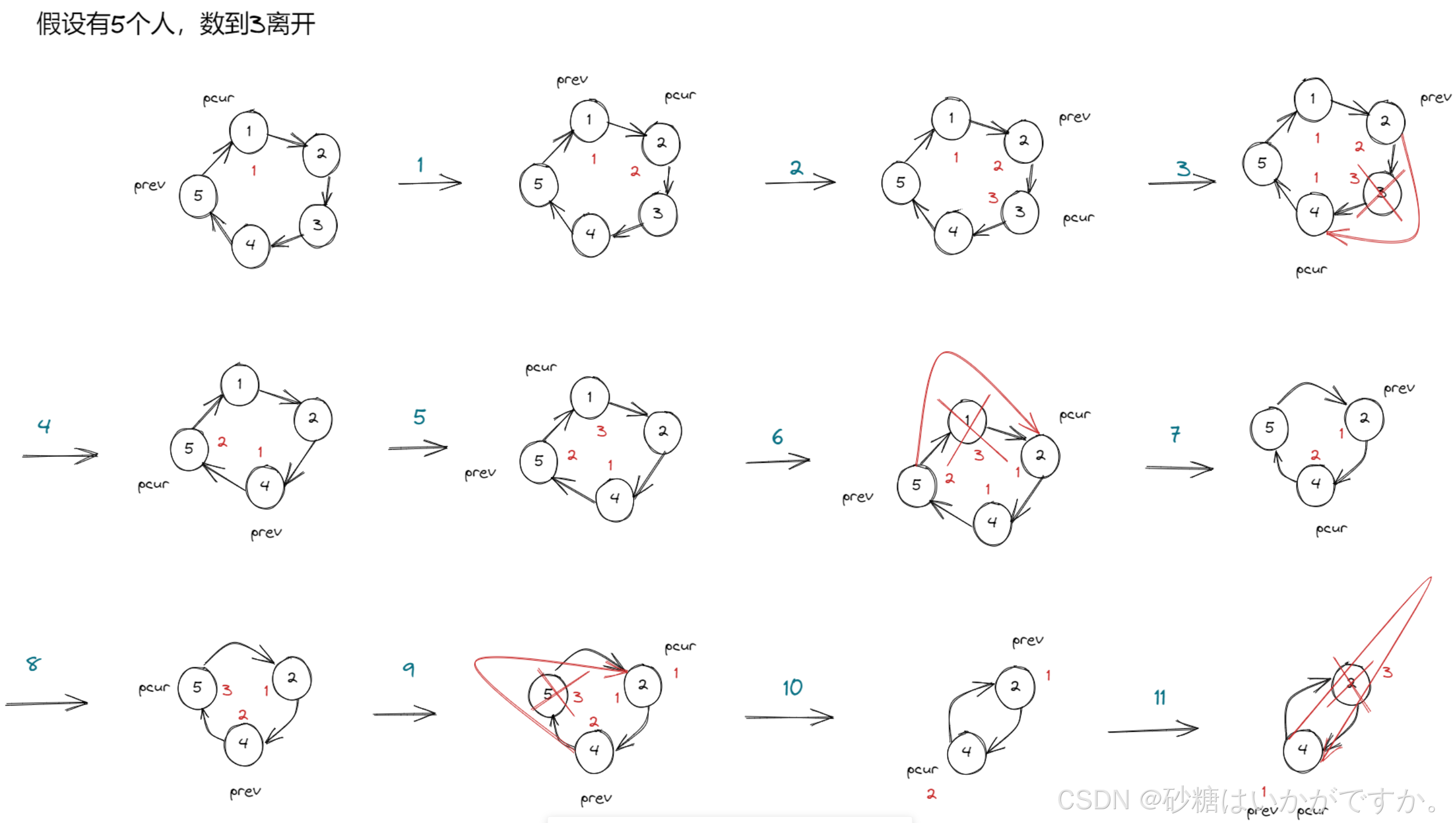
关于题目的思路如下:
- 创建环形链表
- 遍历链表开始计数
- 每数到 m 的那个节点释放掉
- 从下一个节点开始重新报数
- 循环这个操作,直到不能再删除
如此,我们便理解了解题的步骤:
初始节点报 1 ,pcur = pcur->next prev = prev->next 报数依次递增,当报数等于 m 时,先将prev->next = pcur->next 再释放 pcur 节点,pcur = prev->next如此循环即可。
int ysf(int n, int m)
{
//根据 n 创建环形链表
ListNode* prev = createCircle(n);
ListNode* pcur = prev->next;
int count = 1;
//当链表中只有一个节点的情况
while (pcur->next != prev)
{
if (count == m)
{
//销毁 pcur 节点
prev->next = pcur->next;
free(pcur);
pcur = prev->next;
count = 1;
}
else
{
//不需要销毁节点
prev = pcur;
pcur = pcur->next;
count++;
}
}
//此时剩下的节点就是要返回的节点的值
return pcur->val;
}一直循环到最后只剩下一个节点时,pcur 与 prev 重合,此时是循环的尽头,当 pcur->next == prev 时跳出循环。
最后,我们来解答一下前面留下的问题, return prev 还是 return pcur
链表是单向循环的,所以直到一个节点便能知道它后面的所有节点。解这道题需要用到某节点与它的前一个节点,如果我们返回头节点,那头节点的前一个节点我们无法快速找到,而返回头节点的前一个节点作为 prev 完美的解决了问题,既能找到头节点,也能作为 prev 直接使用了。