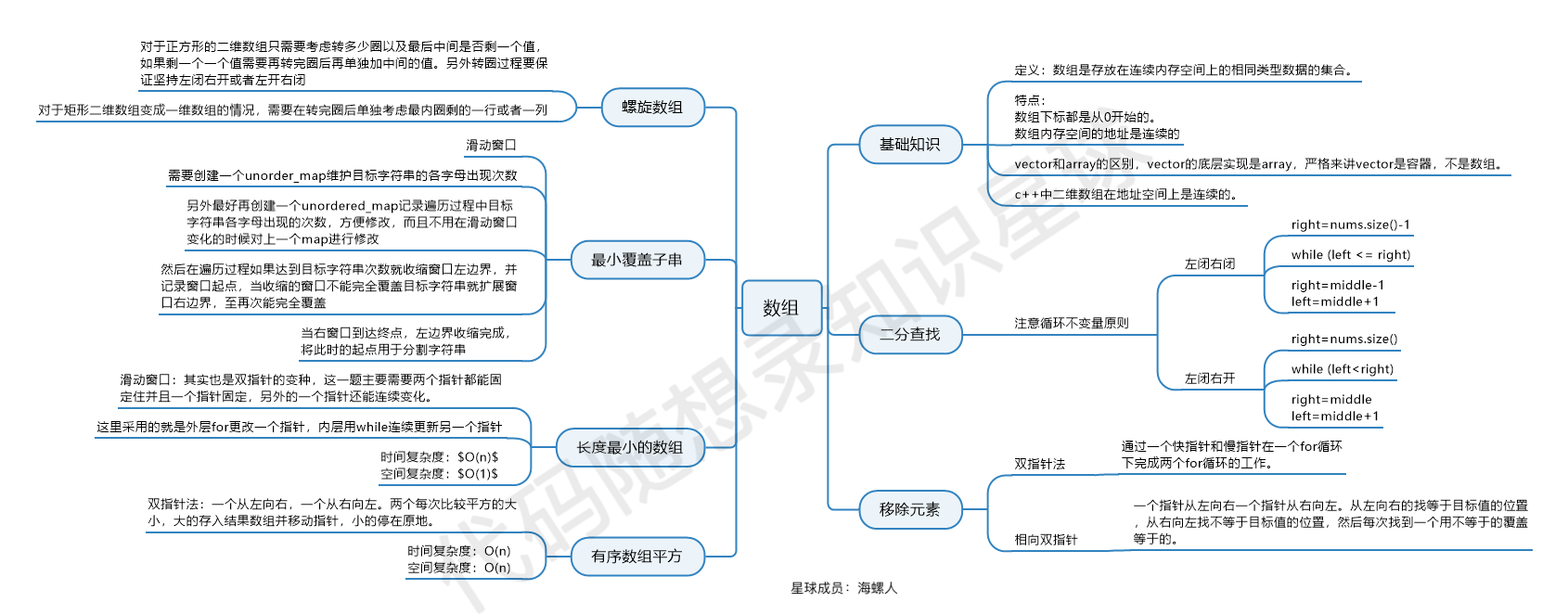
代码随想录算法训练营第二天：数组的再学习

今天继续是对数组进行学习，首先接到的题目是来自leetcode编号为977的有序数组的平方，这道题在昨天的拓展练习中，我已经写过了，在这里跟大家分享一下，首先介绍一下题目：

‍

力扣题目链接(opens new window)

给你一个按非递减顺序排序的整数数组 nums，返回每个数字的平方组成的新数组，要求也按非递减顺序排序。

示例 1：

输入：nums = [-4,-1,0,3,10]
输出：[0,1,9,16,100]
解释：平方后，数组变为 [16,1,0,9,100]，排序后，数组变为 [0,1,9,16,100]

示例 2：

输入：nums = [-7,-3,2,3,11]
输出：[4,9,9,49,121]

对于本题我直观的想法是进行暴力求解，先将数进行平方再进行排序，输出就可以达到想要的结果，这里代码为c++示例：

class Solution{
public:
    vector<int> sortedSquares(vector<int>& A){
        for (int i = 0;i<A.size();i++){
            A[i] *= A[i];
        }
        sort(A.begin(),A.end());//这里直接排序
        return A;
    }
};

c语言则需要手写一份排序出来，这里可以用快速排序：

void quickSort(int arr[],int low,int high){
    if (low >= high) return;
    int i = low,j = high,key = arr[low];
    while (i < j){
        while (i < j && arr[j] >= key) j--;
        arr[i] = arr[j];
        while (i < j && arr[i] <= key) i++;
        arr[j] = arr[i];
    }
    arr[i] = key;
    quickSort(arr,low,i-1);
    quickSort(arr,i+1,high);
}//在这里简单示意快速排序的方法

那么有无更简便的方法去化简这个时间复杂度呢

这里我们采用的是：

双指针法

数组其实是有序的，只不过负数平方之后可能成为最大数了。

那么数组平方的最大值就在数组的两端，不是最左边就是最右边，不可能是中间。

此时可以考虑双指针法了，i指向起始位置，j指向终止位置。

定义一个新数组result，和A数组一样的大小，让k指向result数组终止位置。

如果A[i] * A[i] < A[j] * A[j] 那么result[k--] = A[j] * A[j]; 。

如果A[i] * A[i] >= A[j] * A[j] 那么result[k--] = A[i] * A[i]; 。

如动画所示：

这里用carl的思路给大家呈现

其实这个思想是很巧妙的，我在看leetcode官方题解的时候，里面第二种的方法也是双指针，但是却很麻烦，他的主要思路是

因为数组已经按照升序排序，那么我们找到正负数交接的位置，这样就可以得到两个有序的子数组，可以使用归并的方法进行排序，

具体地，使用两个指针分别指向位置分界线前后，每次比较两个指针对应的数，选择较小的那个放入答案并移动指针，当某一指针移动到边界时，将另一个指针还未遍历到的数依次放入答案，（这里简单实现一个归并排序）

void merge(int arr[],int left,int mid,int right){
    int len1 = mid - left + 1;
    int len2 = right - mid;
    int *L = new int[len1];
    int *R = new int[len2];
    for (int i = 0;i<len1;i++){
        L[i] = arr[left+i];
    }
    for (int j = 0;j<len2;j++){
        R[j] = arr[mid+1+j];
    }
    int i = 0,j = 0;
}

这里给大家实现双指针的两种写法：

卡尔双指针：

class Solution {
public:
    vector<int> sortedSquares(vector<int>& A) {
        int k = A.size() - 1;
        vector<int> result(A.size(), 0);
        for (int i = 0, j = A.size() - 1; i <= j;) { // 注意这里要i <= j，因为最后要处理两个元素
            if (A[i] * A[i] < A[j] * A[j])  {
                result[k--] = A[j] * A[j];
                j--;
            }
            else {
                result[k--] = A[i] * A[i];
                i++;
            }
        }
        return result;
    }
};

归并双指针：

class Solution {
public:
    vector<int> sortedSquares(vector<int>& nums) {
        int n = nums.size();
        int negative = -1;
        for (int i = 0; i < n; ++i) {
            if (nums[i] < 0) {
                negative = i;
            } else {
                break;
            }
        }

        vector<int> ans;
        int i = negative, j = negative + 1;
        while (i >= 0 || j < n) {
            if (i < 0) {
                ans.push_back(nums[j] * nums[j]);
                ++j;
            }
            else if (j == n) {
                ans.push_back(nums[i] * nums[i]);
                --i;
            }
            else if (nums[i] * nums[i] < nums[j] * nums[j]) {
                ans.push_back(nums[i] * nums[i]);
                --i;
            }
            else {
                ans.push_back(nums[j] * nums[j]);
                ++j;
            }
        }

        return ans;
    }
};

那么这道题就差不多结束了，结尾carl给大家的建议：

这里还是说一下，大家不必太在意leetcode上执行用时，打败多少多少用户，这个就是一个玩具，非常不准确。

做题的时候自己能分析出来时间复杂度就可以了，至于leetcode上执行用时，大概看一下就行，只要达到最优的时间复杂度就可以了，

一样的代码多提交几次可能就击败百分之百了…

‍

那么下一题就是对应leetcode209题的：

209.长度最小的子数组

力扣题目链接(opens new window)

给定一个含有 n 个正整数的数组和一个正整数 s ，找出该数组中满足其和 ≥ s 的长度最小的连续子数组，并返回其长度。如果不存在符合条件的子数组，返回 0。

示例：

输入：s = 7, nums = [2,3,1,2,4,3]
输出：2
解释：子数组 [4,3] 是该条件下的长度最小的子数组。

提示：

1 <= target <= 10^9
1 <= nums.length <= 10^5
1 <= nums[i] <= 10^5

对于本题依旧可运用暴力的思想，也就是把所有大于该数的可能都列举出来然后进行比较，选出最小子序列

这个过程需要两个for循环：

c++代码：

class Solution{
public:
    int minSubArrayLen(int s,vector<int>& nums){
        int n = nums.size();
        if(n == 0){
            return 0;
        }
        int ans = INT_MAX;
        for(int i = 0; i< n;i++){
            int sum = 0;
            for (int j = 0;j < n;j++){
                sum += nums[j];
                if (sum >= s){
                    ans = min(ans,j-i+1);
                    break;
                }
            }
        }
        return ans = INT_MAX ? 0: ans;
    }
};
/*INT_MAX 是 C 和 C++ 语言中定义在 <limits.h> 或 <climits> 头文件中的一个宏，
代表一个 int 类型变量能够存储的最大正整数值。这个值是由具体的系统和编译器实现决定的，
但是标准保证它至少为 32767。在许多现代的 32 位和 64 位系统上，INT_MAX 通常是 2,147,483,647（即 (2^{31} - 1)），
因为在这些系统中 int 通常被定义为 32 位。

那么对于这道题，下一个解法是利用前缀和+二分查找：

要使用二分查找，需要额外创建一个数组，这个数组存储nums的前缀和，对这个数组命名arr,arr[i]表示从nums[0]

到nums[i-1]的元素和，这个有什么用呢，其实你可以想到，我们要求的target 其实就是由arr[i]-arr[j]差值所组成的

那么这里我们只是需要通过二分查找，找到，大于或者等于后者下标，使得差值>=target,即可；

因为这道题保证了数组中每个元素都为正，所以前缀和一定是递增的，这一点保证了二分的正确性。如果题目没有说明数组中每个元素都为正，这里就不能使用二分来查找这个位置了。

在很多语言中，都有现成的库和函数来为我们实现这里二分查找大于等于某个数的第一个位置的功能，比如 C++ 的 lower_bound，Java 中的 Arrays.binarySearch，C# 中的 Array.BinarySearch，Python 中的 bisect.bisect_left。但是有时面试官可能会让我们自己实现一个这样的二分查找函数，这里给出一个 C# 的版本，供读者参考：

private int LowerBound(int[] a, int l, int r, int target) 
{
    int mid = -1, originL = l, originR = r;
    while (l < r) 
    {
        mid = (l + r) >> 1;
        if (a[mid] < target) l = mid + 1;
        else r = mid;
    } 

    return (a[l] >= target) ? l : -1;
}

对于这道题的代码：

class Solution{
public:
    int minSubArrayLen(int s,vector<int>& nums){
        int n = nums.size();
        if (n == 0)
            return 0;
        int ans = INT_MAX;
        vector <int> sums(n+1,0);
        // 为了方便计算，令 size = n + 1
        // sums[0] = 0 意味着前 0 个元素的前缀和为 0
        // sums[1] = A[0] 前 1 个元素的前缀和为 A[0]
        // 以此类推
        for (int i = 1;i<=n;i++){
            sums[i] = sums[i-1]+nums[i-1];
        }
        for(int i = 1;i<=n;i++){
            int target = s + sums[i-1];
            auto bound = lower_bound(sums.begin(),sums.end(),target);
            if (bound != sums.end()){
                ans = min(ans,
                static_cast<int>((bound-sums.begin())-(i-1)));
            }
        }
        return ans == INT_MAX ? 0 : ans;
    }
};

我还不是很熟练，本周会继续学习这方面

下面一种方法是用到滑动窗口的思想，来看看carl的讲解:

所谓滑动窗口，就是不断的调节子序列的起始位置和终止位置，从而得出我们要想的结果。

在暴力解法中，是一个for循环滑动窗口的起始位置，一个for循环为滑动窗口的终止位置，用两个for循环完成了一个不断搜索区间的过程。

那么滑动窗口如何用一个for循环来完成这个操作呢。

首先要思考如果用一个for循环，那么应该表示滑动窗口的起始位置，还是终止位置。

如果只用一个for循环来表示滑动窗口的起始位置，那么如何遍历剩下的终止位置？

此时难免再次陷入暴力解法的怪圈。

所以只用一个for循环，那么这个循环的索引，一定是表示滑动窗口的终止位置。

那么问题来了，滑动窗口的起始位置如何移动呢？

这里还是以题目中的示例来举例，s=7，数组是 2，3，1，2，4，3，来看一下查找的过程：

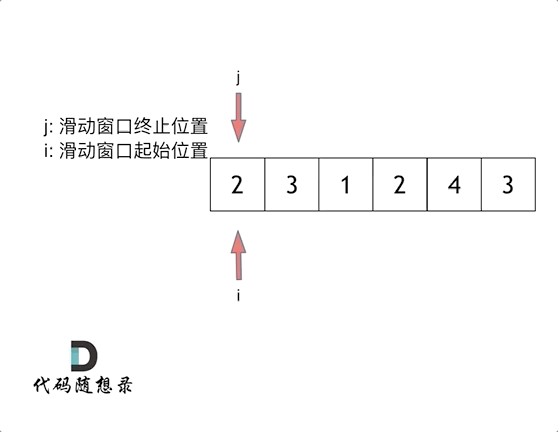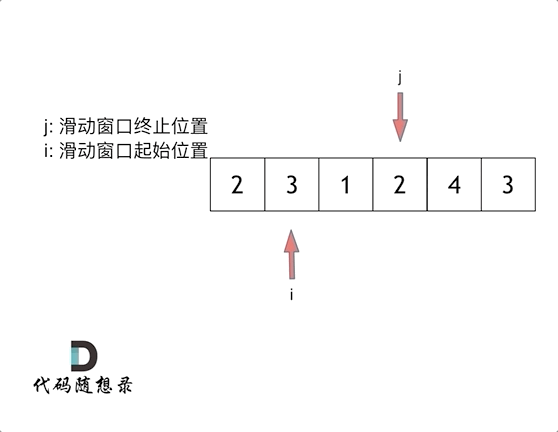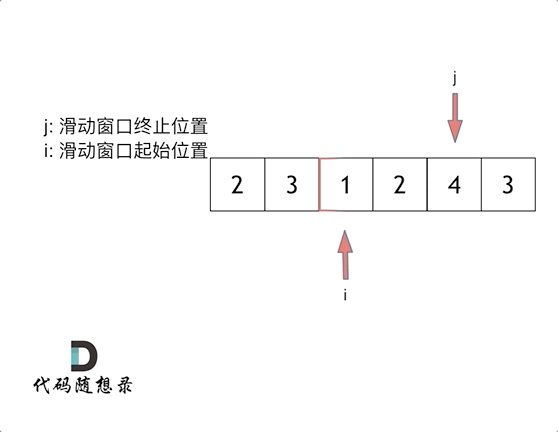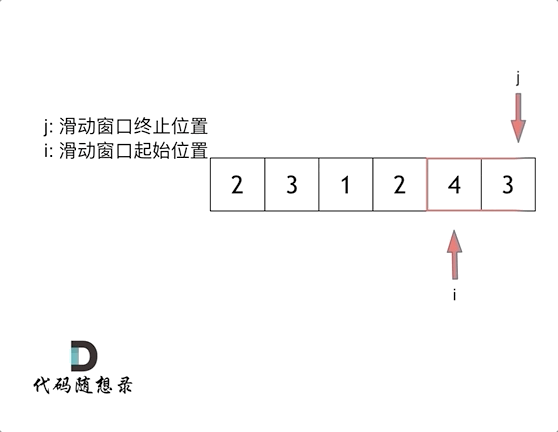
209.长度最小的子数组

最后找到 4，3 是最短距离。

其实从动画中可以发现滑动窗口也可以理解为双指针法的一种！只不过这种解法更像是一个窗口的移动，所以叫做滑动窗口更适合一些。

在本题中实现滑动窗口，主要确定如下三点：

窗口内是什么？
如何移动窗口的起始位置？
如何移动窗口的结束位置？

窗口就是满足其和 ≥ s 的长度最小的连续子数组。

窗口的起始位置如何移动：如果当前窗口的值大于等于s了，窗口就要向前移动了（也就是该缩小了）。

窗口的结束位置如何移动：窗口的结束位置就是遍历数组的指针，也就是for循环里的索引。

解题的关键在于窗口的起始位置如何移动，如图所示：

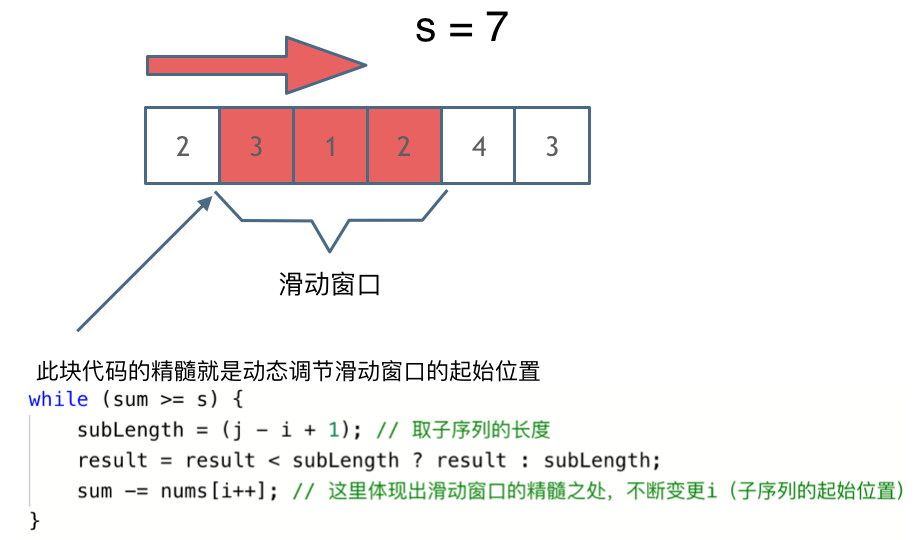
leetcode_209

可以发现滑动窗口的精妙之处在于根据当前子序列和大小的情况，不断调节子序列的起始位置。从而将O(n^2)暴力解法降为O(n)。

class Solution {
public:
    int minSubArrayLen(int s, vector<int>& nums) {
        int result = INT32_MAX;
        int sum = 0; // 滑动窗口数值之和
        int i = 0; // 滑动窗口起始位置
        int subLength = 0; // 滑动窗口的长度
        for (int j = 0; j < nums.size(); j++) {
            sum += nums[j];
            // 注意这里使用while，每次更新 i（起始位置），并不断比较子序列是否符合条件
            while (sum >= s) {
                subLength = (j - i + 1); // 取子序列的长度
                result = result < subLength ? result : subLength;
                sum -= nums[i++]; // 这里体现出滑动窗口的精髓之处，不断变更i（子序列的起始位置）
            }
        }
        // 如果result没有被赋值的话，就返回0，说明没有符合条件的子序列
        return result == INT32_MAX ? 0 : result;
    }
};

用c语言的滑动窗口:

int minSubArrayLen(int target, int* nums, int numsSize){
    //初始化最小长度为INT_MAX
    int minLength = INT_MAX;
    int sum = 0;

    int left = 0, right = 0;
    //右边界向右扩展
    for(; right < numsSize; ++right) {
        sum += nums[right];
        //当sum的值大于等于target时，保存长度，并且收缩左边界
        while(sum >= target) {
            int subLength = right - left + 1;
            minLength = minLength < subLength ? minLength : subLength;
            sum -= nums[left++];
        }
    }
    //若minLength不为INT_MAX，则返回minLnegth
    return minLength == INT_MAX ? 0 : minLength;
}

那么最后我们将迎来一道特殊题目，螺旋矩阵

59.螺旋矩阵II

力扣题目链接(opens new window)

给定一个正整数 n，生成一个包含 1 到 n^2 所有元素，且元素按顺时针顺序螺旋排列的正方形矩阵。

示例:

输入: 3 输出: [ [ 1, 2, 3 ], [ 8, 9, 4 ], [ 7, 6, 5 ] ]

这道题跟贪吃蛇的游戏设置程序是一个原理，那么在这里并不涉及到什么算法，就是模拟过程，但却十分考察对代码的掌控能力。

那么要如何实现这个矩阵呢，我们要进行分类讨论，现在外侧一个边一个边的填充到内侧，

注意这里一个边要填充的个数跟边长的不一样的，应该是边长减1，因为我们每条边都共用一个顶点

求解本题依然是要坚持循环不变量原则。

模拟顺时针画矩阵的过程:

填充上行从左到右
填充右列从上到下
填充下行从右到左
填充左列从下到上

由外向内一圈一圈这么画下去。

可以发现这里的边界条件非常多，在一个循环中，如此多的边界条件，如果不按照固定规则来遍历，那就是一进循环深似海，从此offer是路人。

这里一圈下来，我们要画每四条边，这四条边怎么画，每画一条边都要坚持一致的左闭右开，或者左开右闭的原则，这样这一圈才能按照统一的规则画下来。

那么我按照左闭右开的原则，来画一圈，大家看一下：

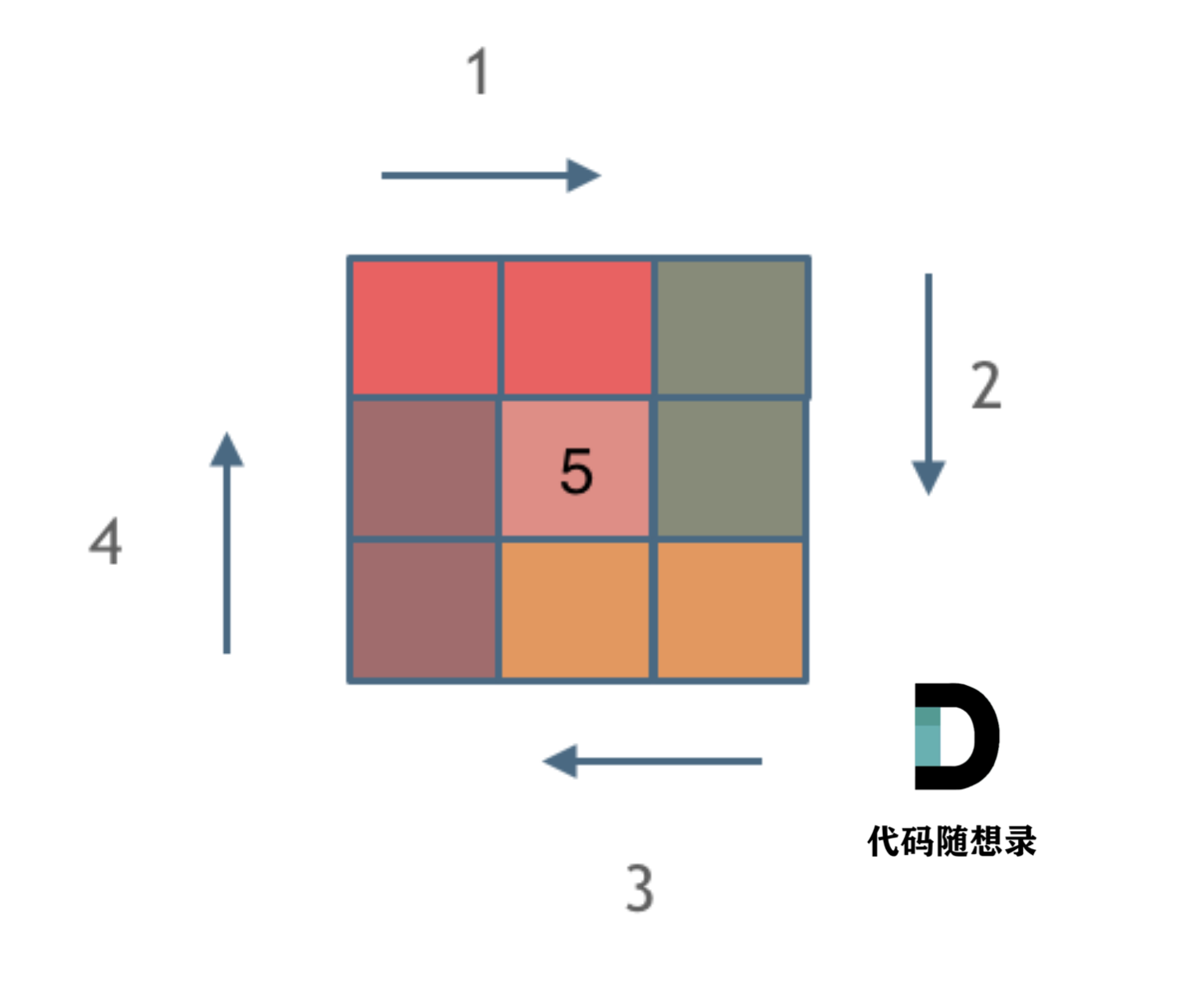
这里每一种颜色，代表一条边，我们遍历的长度，可以看出每一个拐角处的处理规则，拐角处让给新的一条边来继续画。

这也是坚持了每条边左闭右开的原则。

代码如下：

class Solution{
public:
    vector<vector<int>> generateMatrix(int n){
        vector<vector<int>>res(n,vector<int>(n,0));//二维数组
        int startx = 0, starty = 0;
        int loop = n/2;
        int mid = n/2;

        /**这里的int mid = n / 2;计算得到的是中间行和中间列的索引（因为行和列的数量相同）。
        由于索引从0开始，所以对于一个3x3的矩阵，n为3，n / 2得到1，中间位置就是(1, 1)；
        对于一个5x5的矩阵，n为5，n / 2得到2，中间位置就是(2, 2)。*/
        int count = 1;
        int offset = 1;
        int i,j;
        while(loop --){
            i = startx;
            j = starty;


for (j;j<n-offset;j++){
    res[i][j] = count++;
}
for(i;i<n-offset;i++){
    res[i][j] = count++;
}
for (;j>starty;j--){
    res[i][j] = count++;
}
for (;i>startx;i--){
    res[i][j] = count++;
}

        startx++;
        starty++;
// offset 控制每一圈里每一条边遍历的长度
        offset += 1;
    } if (n % 2) {
            res[mid][mid] = count;
        }
        return res;
    }
};

这里leetcode官方题解给出了一种按层模拟的方法：

可以将矩阵看成若干层，首先填入矩阵最外层的元素，其次填入矩阵次外层的元素，直到填入矩阵最内层的元素。

定义矩阵的第 kkk 层是到最近边界距离为 kkk 的所有顶点。例如，下图矩阵最外层元素都是第 111 层，次外层元素都是第 222 层，最内层元素都是第 333 层。

[[1, 1, 1, 1, 1, 1],
 [1, 2, 2, 2, 2, 1],
 [1, 2, 3, 3, 2, 1],
 [1, 2, 3, 3, 2, 1],
 [1, 2, 2, 2, 2, 1],
 [1, 1, 1, 1, 1, 1]]

对于每层，从左上方开始以顺时针的顺序填入所有元素。假设当前层的左上角位于 (top,left)(\textit{top}, \textit{left}) (top,left)，右下角位于 (bottom,right)(\textit{bottom}, \textit{right}) (bottom,right)，按照如下顺序填入当前层的元素。

从左到右填入上侧元素，依次为 (top,left)(\textit{top}, \textit{left}) (top,left) 到 (top,right)(\textit{top}, \textit{right}) (top,right)。
从上到下填入右侧元素，依次为 (top+1,right)(\textit{top} + 1, \textit{right}) (top+1,right) 到 (bottom,right)(\textit{bottom}, \textit{right}) (bottom,right)。
如果 left<right\textit{left} < \textit{right} left < right 且 top<bottom\textit{top} < \textit{bottom} top < bottom，则从右到左填入下侧元素，依次为 (bottom,right−1)(\textit{bottom}, \textit{right} - 1) (bottom,right−1) 到 (bottom,left+1)(\textit{bottom}, \textit{left} + 1) (bottom,left+1)，以及从下到上填入左侧元素，依次为 (bottom,left)(\textit{bottom}, \textit{left}) (bottom,left) 到 (top+1,left)(\textit{top} + 1, \textit{left}) (top+1,left)。

填完当前层的元素之后，将 left\textit{left} left 和 top\textit{top} top 分别增加 111，将 right\textit{right} right 和 bottom\textit{bottom} bottom 分别减少 111，进入下一层继续填入元素，直到填完所有元素为止。

class Solution {
public:
    vector<vector<int>> generateMatrix(int n) {
        int num = 1;
        vector<vector<int>> matrix(n, vector<int>(n));
        int left = 0, right = n - 1, top = 0, bottom = n - 1;
        while (left <= right && top <= bottom) {
            for (int column = left; column <= right; column++) {
                matrix[top][column] = num;
                num++;
            }
            for (int row = top + 1; row <= bottom; row++) {
                matrix[row][right] = num;
                num++;
            }
            if (left < right && top < bottom) {
                for (int column = right - 1; column > left; column--) {
                    matrix[bottom][column] = num;
                    num++;
                }
                for (int row = bottom; row > top; row--) {
                    matrix[row][left] = num;
                    num++;
                }
            }
            left++;
            right--;
            top++;
            bottom--;
        }
        return matrix;
    }
};

总结

‍