为什么要引入图这个概念?先让我们了解一下图的应用场景
- 计算机视觉:在图像和视频分析中,图可以用来表示图像中的对象和它们之间的关系。通过图的算法,可以进行对象识别、场景理解等。
- 软件工程:在软件系统中,图可以用来表示类之间的关系、模块之间的依赖等。通过图的算法,可以进行代码重构、依赖分析等。
- 电力系统:在电力网络中,图可以用来表示电网中的节点(发电站、变电站等)和边(输电线)。通过图的算法,可以进行电网优化、故障检测等。
- 物流和供应链管理:在物流和供应链管理中,图可以用来表示仓库、配送中心、运输路线等。通过图的算法,可以进行路径规划、库存优化等。
- 经济学和金融学:在经济学和金融学中,图可以用来表示市场中的交易网络、投资关系等。通过图的算法,可以进行市场分析、风险评估等。
图的应用场景非常广泛,几乎所有涉及复杂关系和网络结构的问题都可以用图来建模和解决。
图的概念和抽象数据类型
1.图的定义和术语
图是由顶点集合和边集合组成的数据结构,图中的数据元素通常称为顶点,顶点之间的关系称为边。一个图G=(V,E),V是顶点vi的集合(0≤i<n),n为顶点数,E是边的集合。
(1)无向图
无向图中的边是没有方向的,通常是用来表示节点间的关系。
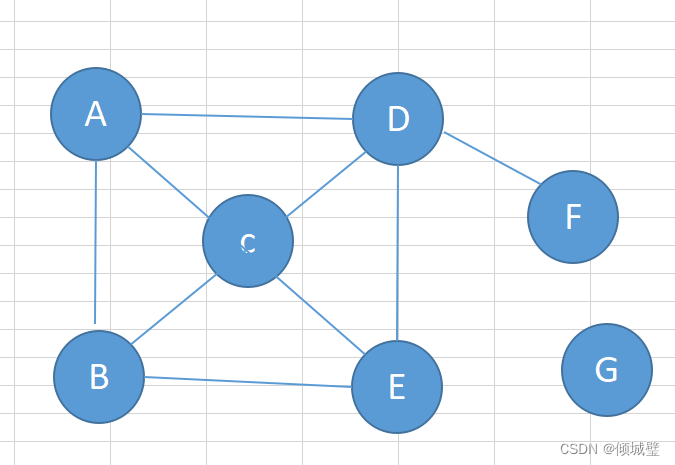
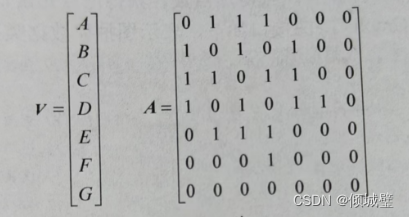
下面是无向图G1
无向图G1的顶点集合V和集合E
顶点的集合:V(G1)={A,B,C,D,E,F,G};
边的集合:E(G1)={(A,B),(A,C)(A,D),(B,C),(B,E),(C,E),(C,D),(D,E),(D,F)}
树是连通的无回路和无向图。假设有一颗树T有n个顶点,则其必有n-1条边。
(2)有向图
有向图或有向图是其中边缘具有特定方向的图数据结构。它们源自一个顶点,最终达到另一个顶点。
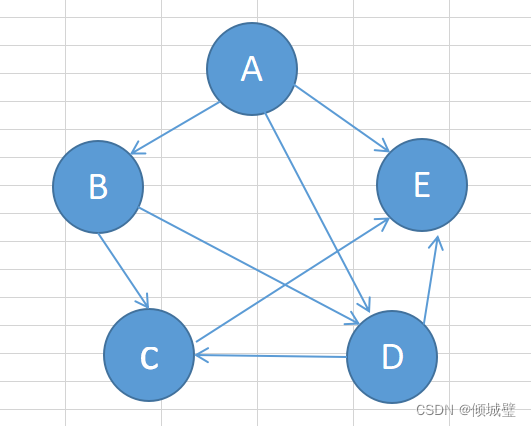
下面是有向图G2
顶点集合:V(G,)={A,B,C,D,E};
边的集合:E(G,)={ <A,B >,< A, D >,< A,E >,< B,C >,< B,D >,< C,E >,<D,C >,<D,E >};
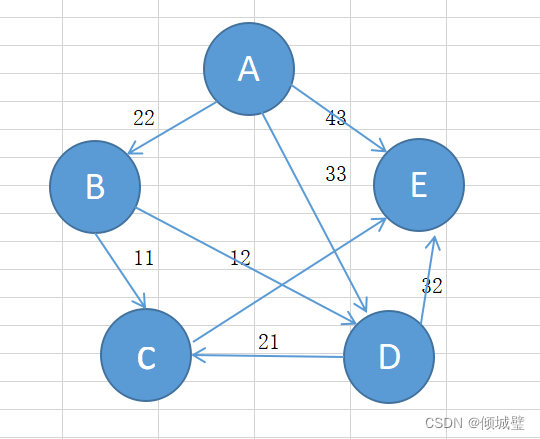
(3)带权图
带权图是指边具有的权值,在不同应用中,权值有着不同的含义,通常表示边上的一种成本,距离,时间或其他量度,带权图可以是无向的也可以是有向的。
(4)邻接节点
若(vi,vj)是无向图中的一条边,就是说两个节点间存在一条边 ,则称vi和vj互为邻接节点,就是说两个节点间存在一条边。
(5)顶点的度
顶点的度是指定点vi相关联的边数,记为degree(vi)。度为0的顶点称为孤立点,度为1的顶点称为悬挂点。
B的度为4,E的度为1(悬挂点),x的度为0(孤立点)。
在有向图中,以vi为终边的边数称为vi的入度,以vi为起点的边数称为vi的出度。比如上面讲到的有向图中的B的入度=1,出度=2。
(6)路径
路径是指一个顶点到另外一个顶点的路线,简单路径是指路径上的各顶点都不重复。
回路是指起点和终点相同且长度大于1的简单路径,回路又称为环,如(A,B,D,C)是一条简单路径,(A,B,C,D)是一条回路。
对于不带权图,路径长度是指路径上的边数。对于带权图,路径长度是指路径上各条边的权值之和。例如下面的(A,B,D,C)路径长度为3。
邻接矩阵
(1)邻接矩阵概念及其表示
图的表示方法有两种:二维数组表示(邻接矩阵);链表表示(邻接表)。
- 如果图的边没有权值,用0表示顶点之间无边,用1表示顶点之间有边。
- 如果图的弧有权值,用无穷大表示顶点之间无边,用权值表示顶点之间有边,同一点之间的权值为0。
通过观察可知,无向图的邻接矩阵是对称点,有向图的邻接矩阵不一定对称
使用邻接矩阵实现图的缺点:
使用邻接矩阵这种弄存储方式的空间复杂度是N^2,所以当处理的问题规模比较大的话,内存空间极有可能不够用,可以发现,当很多边不存在的时候,内存空间同样需要存储数据,这样会造成空间的一定损失。
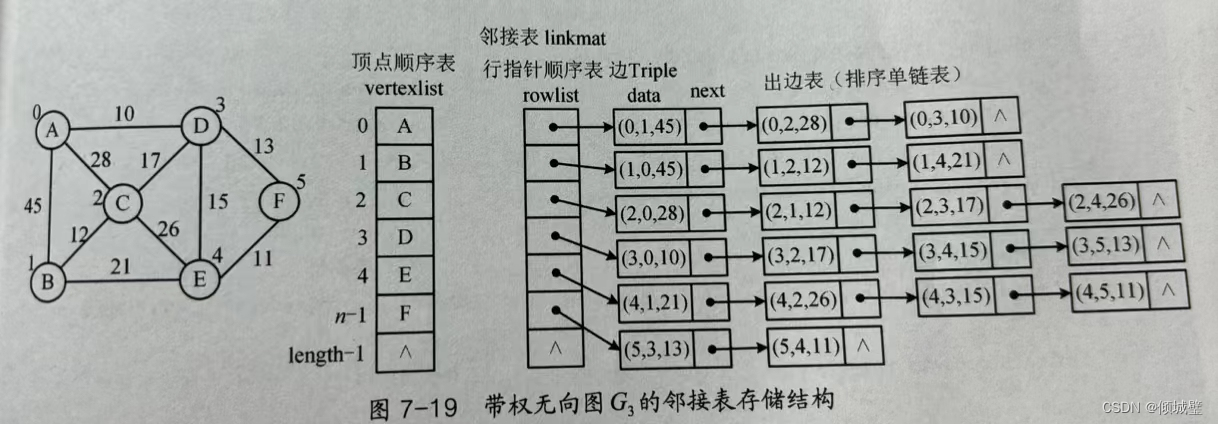
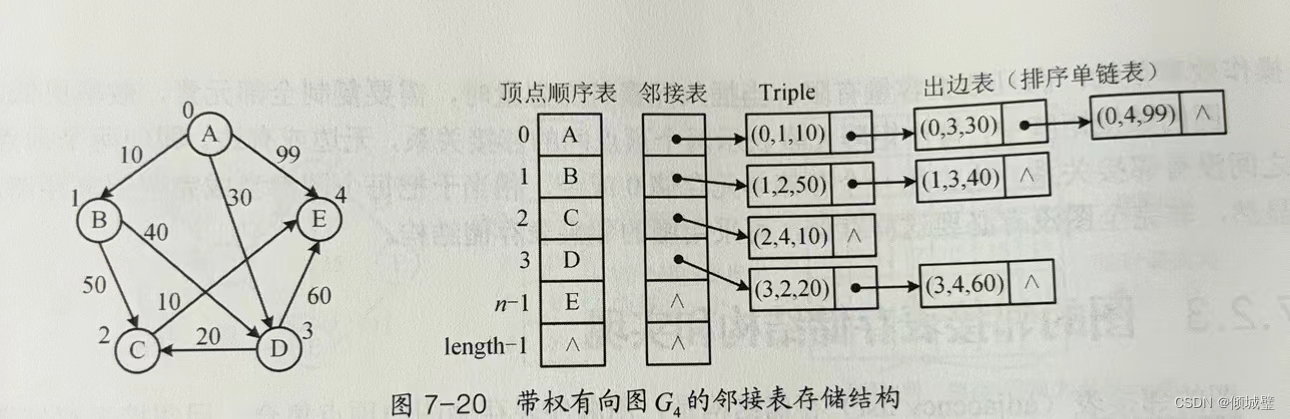
(2)邻接表
针对上面邻接矩阵比较浪费内存空间的问题,诞生了图的另外一种存储方法—邻接表 。
邻接表只关心存在的边,不关心不存在的边。
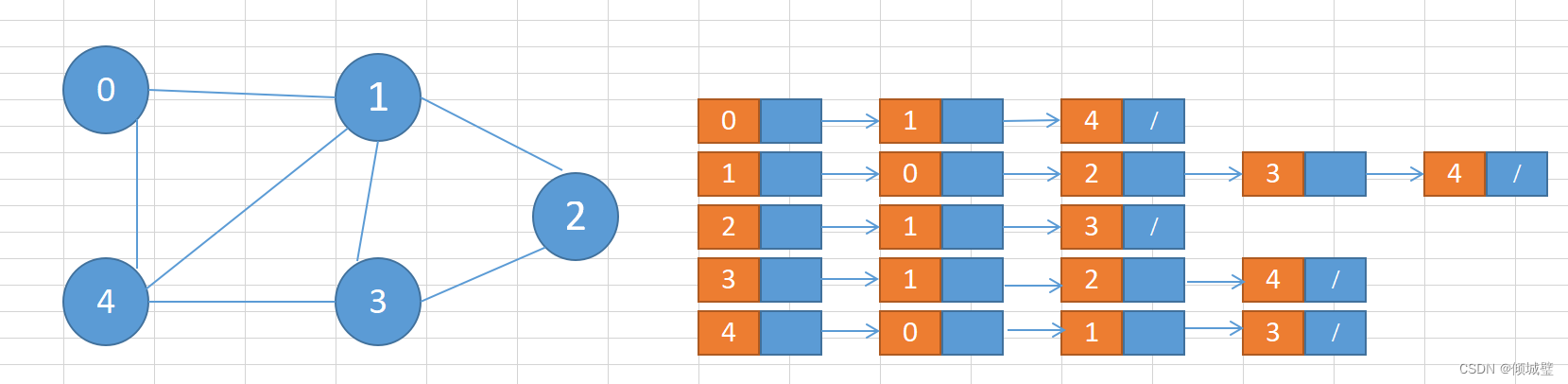
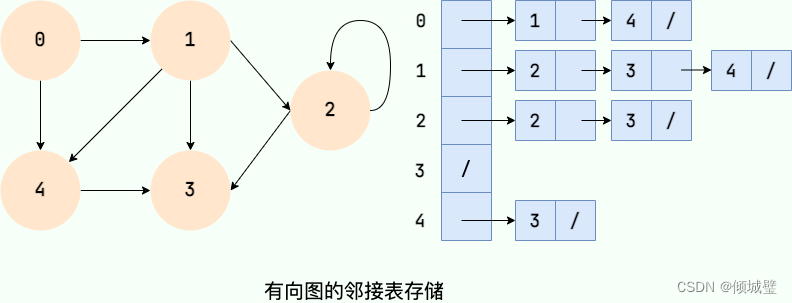
邻接链表使用一个链表来存储某个顶点的所有后继相邻顶点。对于图中每个顶点 Vi,把所有邻接于 Vi 的顶点 Vj 链成一个单链表,这个单链表称为顶点 Vi 的 邻接表。如下图所示:
- 在无向图中,邻接表元素个数等于边的条数的两倍,如左图所示的无向图中,边的条数为 7,邻接表存储的元素个数为 14。
- 在有向图中,邻接表元素个数等于边的条数,如右图所示的有向图中,边的条数为 8,邻接表存储的元素个数为 8。
图的遍历
图的深度优先搜索策略
图的遍历是指从图中的某个顶点vi出发,沿着途中的边前行,到达并访问途中所有的顶点,且每个顶点仅被访问一次。
遍历图比较复杂,我们需要考虑下面三个问题并提供解决办法
- 指定遍历的起始访问顶点,可从图G中任意一个顶点vi出发
- 由于一个顶点与多个顶点相邻,因此要在多个邻接顶点之间约定一种访问次序。通常按照定点的存储顺序进行遍历。
- 由于图中存在回路,在访问某个顶点后,可能沿着某条路径又回到该顶点。因此,为了避免重复访问同一个顶点,在遍历过程中必须对访问过的顶点进行标记。通常,设置一个标记数组来记录每个顶点是否被访问过。
深度优先搜索(Depth First Search ,DFS)策略遍历图G一个连通分量的规则如下,从其中一个顶点vi出发,访问顶点vi;寻找下一个未被访问的邻接顶点vj,再从vj遍历图G;继续,直到访问了图G从顶点vi出发的一个连通分量。
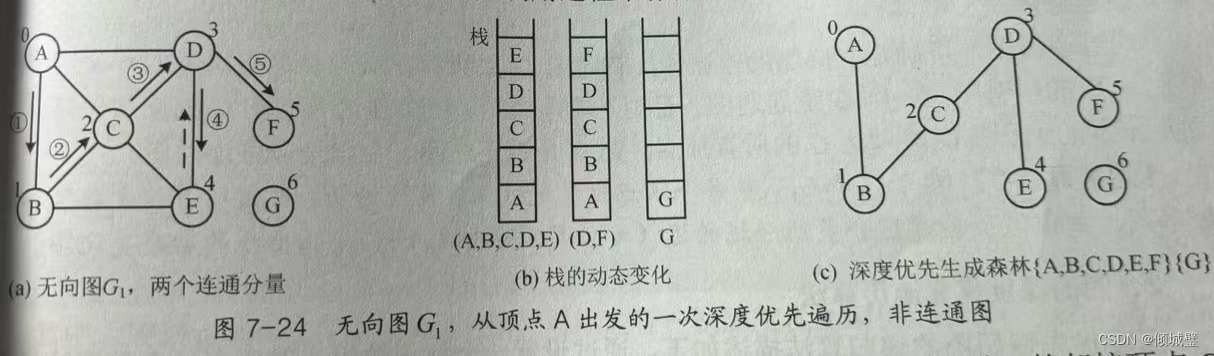
(1)无向图的深度优先搜索
深度优先搜索跟递归类似,你们先可以去了解一下递归再来看深度优先搜索会更加好理解。
最初是从A点开始遍历,从B-C-D-F这样的顺序遍历,每一个访问顶点入栈,记录递归调用的执行路径。
当栈的顶点E没有被下一个未被访问的邻接顶点时,E出栈,递归返回之前的顶点D,再去寻找顶点D的邻接节点F(未被访问)。
此时,从顶点A出发的一次深度优先搜索(A,B,C,D,E,F),遍历了G1的一个连通分量,由两条路径(A,B,C,D,E)和(D,F)组成了该连通分量的一颗深度优先生成树。以深度优先搜索遍历得到的生成树,称为深度优先生成树。
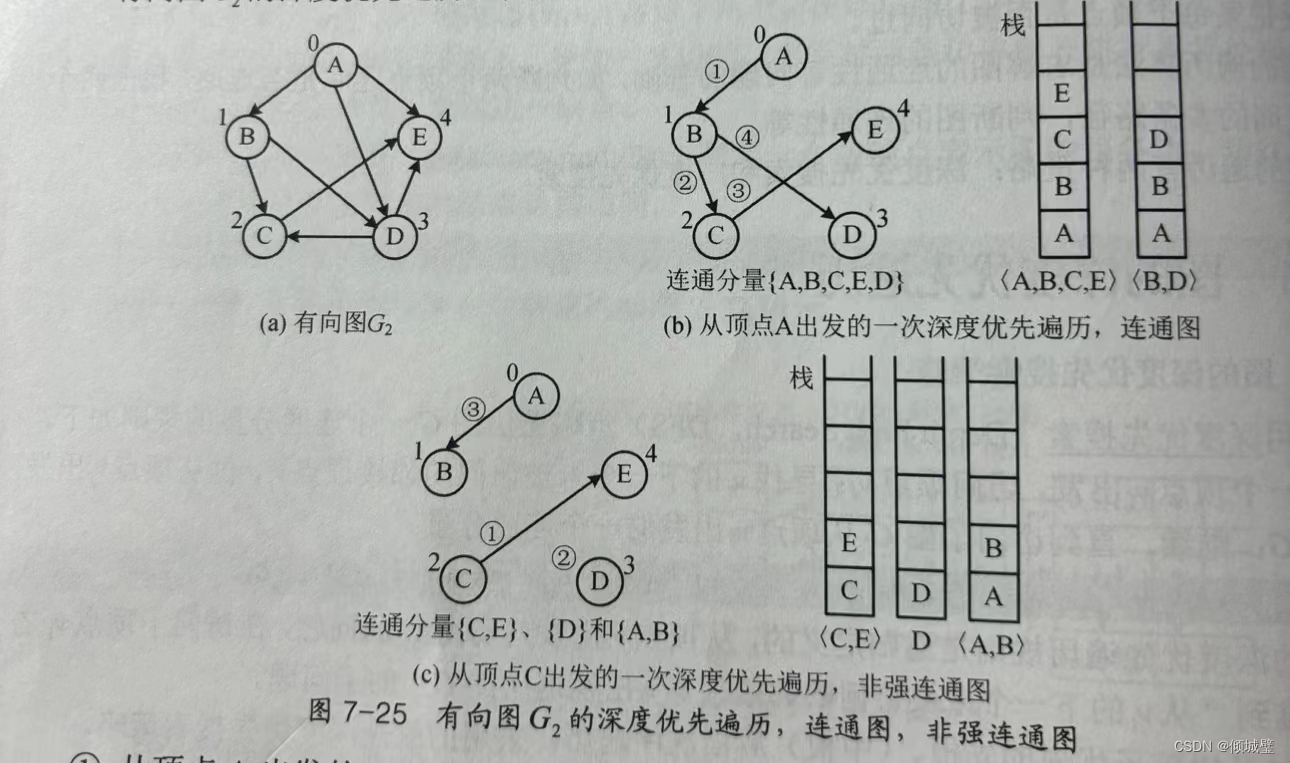
(2)有向图的深度优先搜索
从顶点A出发一次深度优先搜索(A,B,C,E,D),由两条路径<A,B,C,E>和<B,D>组成,访问了G2的所有顶点,所以有向图G2是连通图。
从顶点C出发,深度优先搜索了3次(C,E),(D),(A,B)才完成遍历,所以有向图是非强连通图。
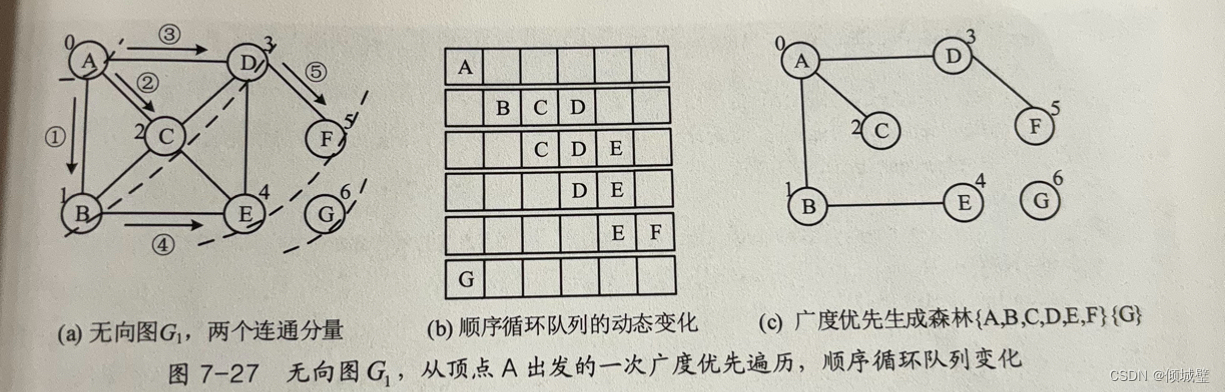
图的广度优先遍历
(1)无向图的广度优先搜索
广度优先遍历(Breadth First Search, BFS)策略遍历图G的规则,就是树的层次遍历算法。
无向图G1从顶点A出发的一次广度优先搜索遍历过程:从A出发,再次访问邻接节点(B,C,D)(未被访问);之后,访问B的邻接顶点E,再访问D的邻接节点F,使用队列存储方式访问顶点和其他邻接节点。
队列的作用是存储当前访问顶点所有邻接顶点,这些顶点排队等待被访问,当访问完当前顶点时,出队一个顶点,即下一个要访问的顶点。
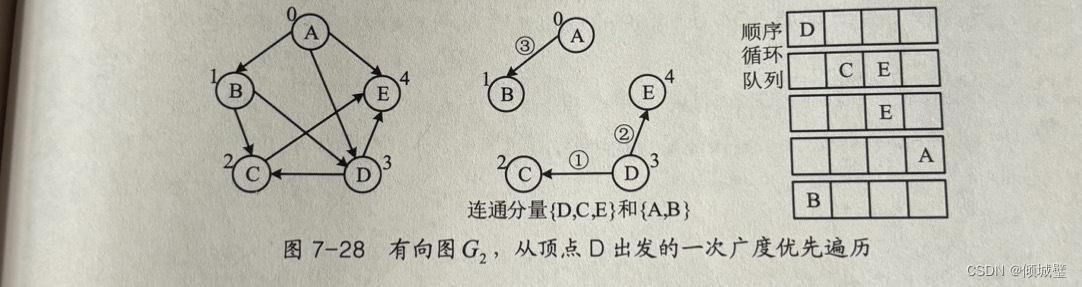
(2)有向图的广度优先搜索
先访问D,再访问D的邻接节点C,E,遍历连通分量(D,C,E);然后从A出发,遍历连通分量(A,B)。
图的深度和广度优先搜索算法
import sun.security.provider.certpath.AdjacencyList;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.LinkedList;
public class AdjacencyMatrix {
private ArrayList<String> vexs;//顶点表
private int[][] edges;//边表
int numVertexes;//顶点的数量
int numEdges;//边的数量
boolean[] visited;
public AdjacencyMatrix(int numVertexes, int numEdges) {
this.vexs = new ArrayList<String>(numVertexes);//用于存储图中的顶点数量
this.edges = new int[numVertexes][numVertexes];//用于存储图中边的数量
this.numVertexes = numVertexes;
this.numEdges = numEdges;
this.visited = new boolean[numVertexes];
}
private void insertVex(String v){
vexs.add(v);//将新的顶点v添加到vexs列表中
}
private void insertEdge(int v1,int v2,int weight){
edges[v1][v2]=weight;
edges[v2][v1]=weight;
}
private void show(){
for(int[] link:edges){
System.out.println(Arrays.toString(link));
}
}
private void DFS(int i){
visited[i]=true;
System.out.print(vexs.get(i)+" ");
for (int j = 0; j < numVertexes; j++) {
if (edges[i][j]>0&&!visited[j]) {
DFS(j);
}
}
}
private void DFSTraverse(){
int i;
for (i = 0; i < numVertexes; i++) {
visited[i]=false;
}
for ( i = 0; i <numVertexes ; i++) {
if(!visited[i]){
DFS(i);
}
}
}
private void BFSTraverse(){
int i ,j ;
LinkedList queue =new LinkedList();
for (i = 0; i < numVertexes; i++) {
visited[i] =false;
}
for(i =0;i<numVertexes;i++){
if(!visited[i]){
visited[i]=true;
System.out.print(vexs.get(i)+" ");
queue.addLast(i);
while (!queue.isEmpty()){
i=(Integer)queue.removeFirst();
for(j =0;j<numVertexes;j++){
if(edges[i][j]>0&&!visited[j]){
visited[j]=true;
System.out.print(vexs.get(j)+" ");
queue.addLast(j);
}
}
}
}
}
}
public static void main(String[] args) {
int numVertexes = 9;
int numEdges = 15;
AdjacencyMatrix graph = new AdjacencyMatrix(numVertexes, numEdges);
graph.insertVex("A");
graph.insertVex("B");
graph.insertVex("C");
graph.insertVex("D");
graph.insertVex("E");
graph.insertVex("F");
graph.insertVex("G");
graph.insertVex("H");
graph.insertVex("I");
graph.insertEdge(0, 1, 1);
graph.insertEdge(0, 5, 1);
graph.insertEdge(1, 2, 1);
graph.insertEdge(1, 6, 1);
graph.insertEdge(1, 8, 1);
graph.insertEdge(2, 3, 1);
graph.insertEdge(2, 8, 1);
graph.insertEdge(3, 4, 1);
graph.insertEdge(3, 6, 1);
graph.insertEdge(3, 7, 1);
graph.insertEdge(3, 8, 1);
graph.insertEdge(4, 7, 1);
graph.insertEdge(4, 5, 1);
graph.insertEdge(5, 6, 1);
graph.insertEdge(6, 7, 1);
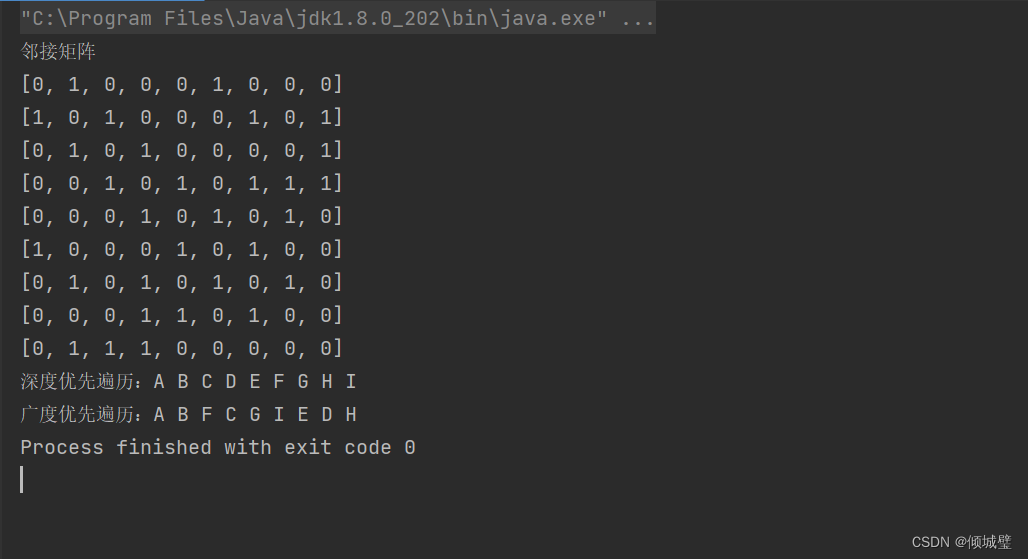
System.out.println("邻接矩阵");
graph.show();
System.out.print("深度优先遍历:");
graph.DFSTraverse();
System.out.println();
System.out.print("广度优先遍历:");
graph.BFSTraverse();
}
}