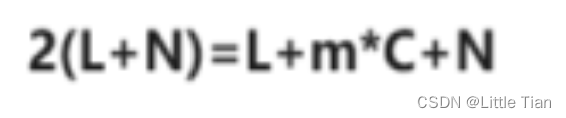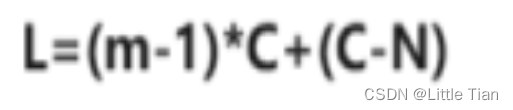证明链表带环
链表的带环问题指的是本该指向NULL的最后一个节点指向了之前的节点,导致链表成环,找不到尾结点的情况,那么我们该如何证明链表带环呢?
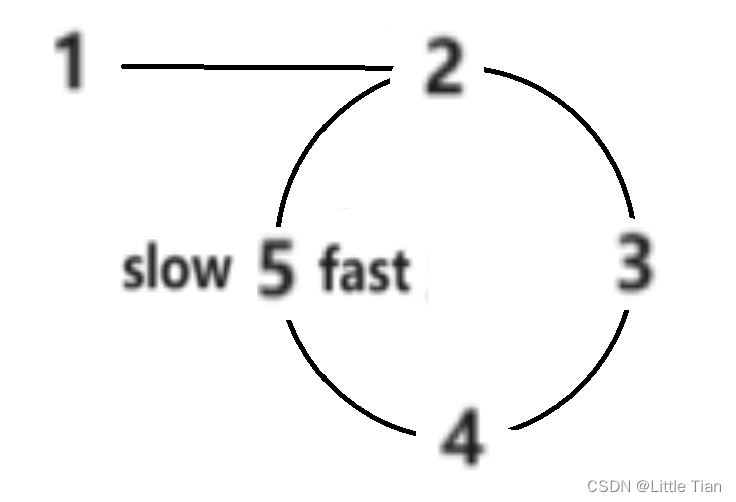
我们可以类比物理中的追及问题,让快慢指针同时走,两者相遇说明有环,两者不相遇(遇见NULL)说明没有环。
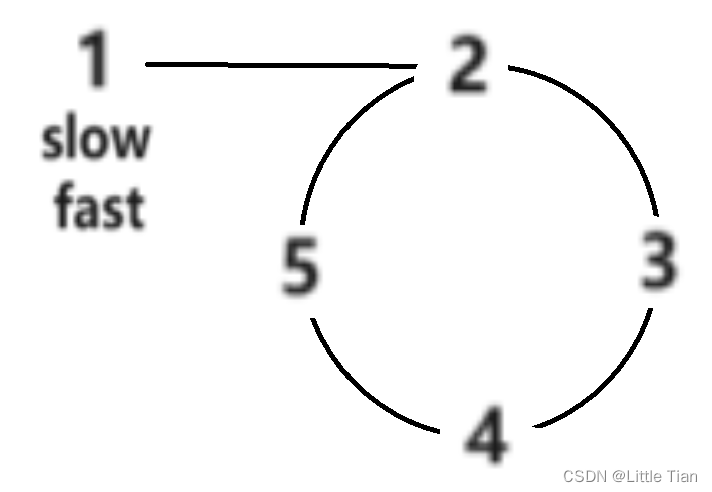
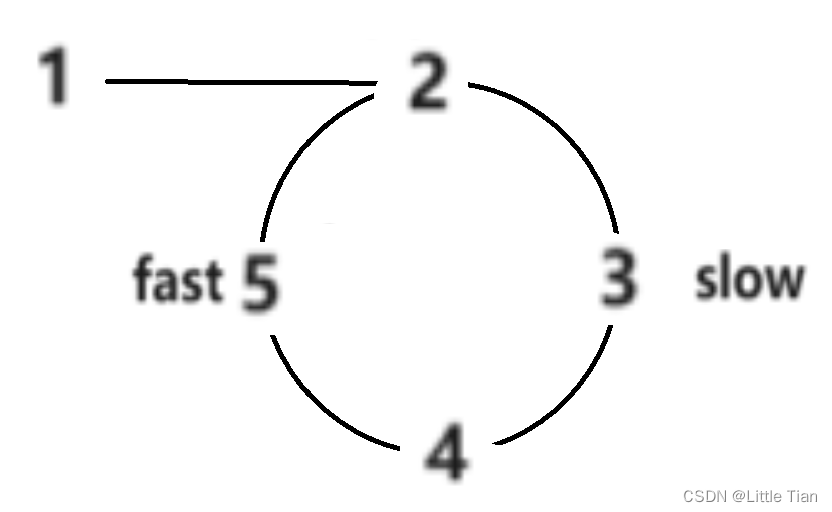
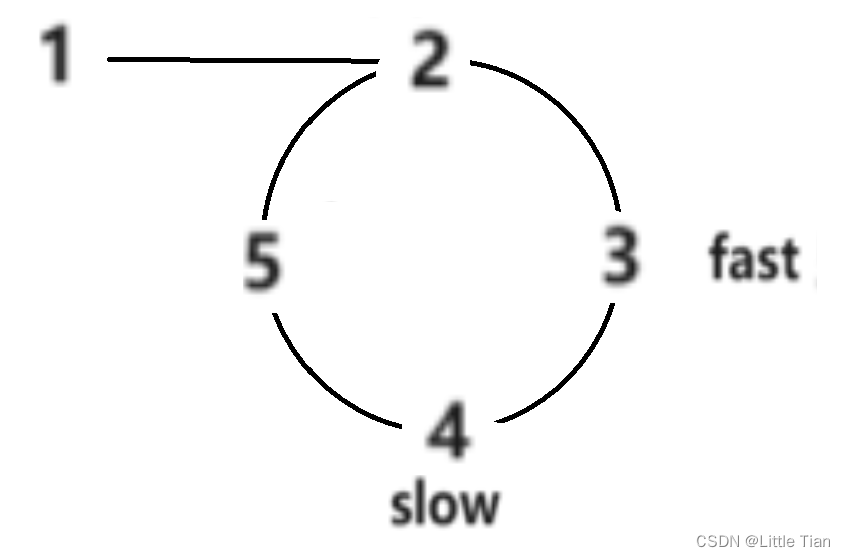
那么应该怎么确保他们相遇呢,我们从快指针一次走两个单位,慢指针一次走一个单位开始,流程图如下:
最后确实是快慢指针相遇。
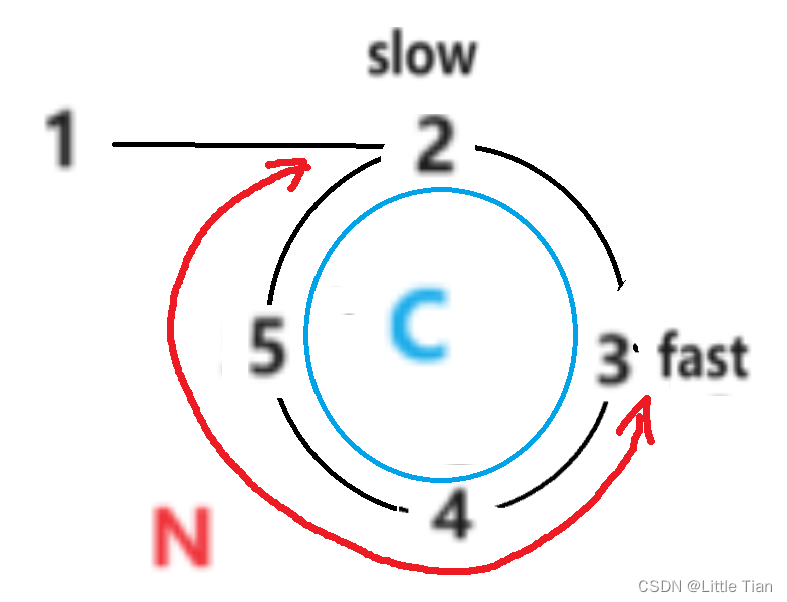
如果是快指针一次走三个单位,慢指针一次走一个单位呢?是不是也可以呢?假设当慢指针进入环的时候,快慢指针的差距为N,环的长度为C。
每迭代一次,如果快指针每次走3个单位,慢指针每次走一个单位,差距就会变成N-2,N-4,N-6,如果N是奇数,则快慢指针不会相遇,当然也有相遇的情况,如果C为奇数,会相遇,这是因为当N和C都为奇数的时候,差距N-2,N-4,最后变为-1(相当于fast指针超过slow指针一个单位),此时距离相当于是C-1(是一个偶数),也就是说,fast指针会超过slow指针一次,然后相遇。
不过上段文字并不十分重要,如果仍然快指针一次走两个单位,慢指针一次走一个单位,那么快慢指针的距离就会是N-1,N-2,N-3,最后变为0。也就是说,如果快指针一次走两个单位,慢指针一次走一个单位,他们总会相遇并且不会存在错过的情况,是判断是否有环的理想方法。
找到环节点
知道了如何判断链表是否有环之后,如何找到入环的节点呢?
方法 1 :
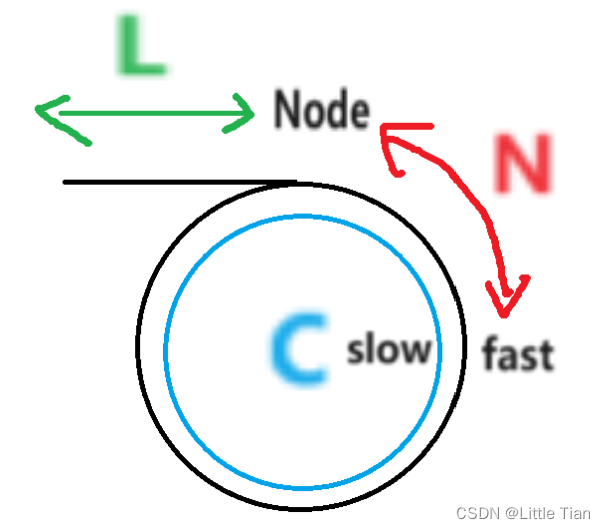
假设当快慢指针相遇的时候,相遇节点距离进入环的节点长度为N,环的周长为C,环前的单链长度为L。如图所示:
当slow指针和fast指针相遇的时候,fast指针的路程是slow指针路程的二倍(因为fast一次走两个单位,slow一次走一个单位),表示slow慢指针的路程就是:L+N,对于快指针来说,如果L足够长,那么有可能当slow慢指针进入环之前,fast快指针就已经在环内遍历了m遍,m>1,所以fast快指针的路程是:L+m*C+N。
二倍的slow慢指针的路程等于fast快指针的路程:
最后变形得到:
(m-1)*C相当于绕环转(m-1)圈,所以也就是说从快慢指针相遇的地方接着走(C-N)个单位(在走m-1圈,位置相当于没变)和L个单位一样,也就是进入环的节点。
所以我们可以借助第一问先找到快慢指针的相遇节点,在让头指针走L个单位,相遇节点走C-N个单位(其实就是让他们走到相等为止),找到进入环的节点。
方法 2 :
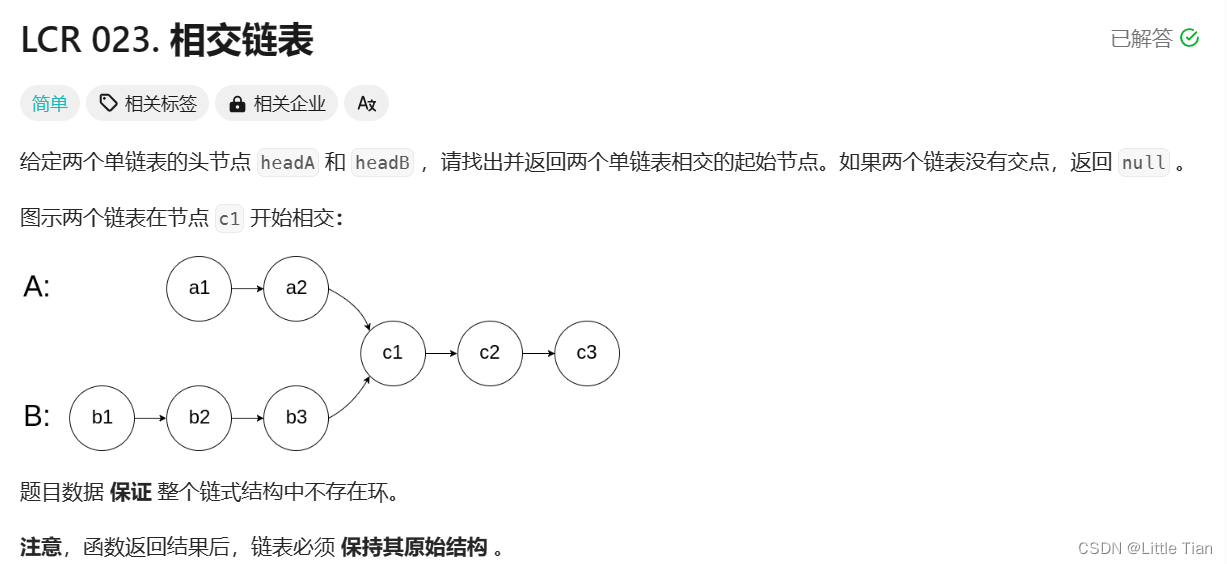
借鉴上面的最后的思路,我们可以将环从相遇节点断开,然后找两个链表的相交节点,请看相交链表:
在这也简单说明一下一般相交链表的思路:就是分别计算不同头指针链表的长度num1,num2,先让长的链表走 |num1-num2| 个单位,再两个链表一起走,直到找到节点。
这就是文章的全部内容了,希望对你有所帮助,如有错误欢迎评论。