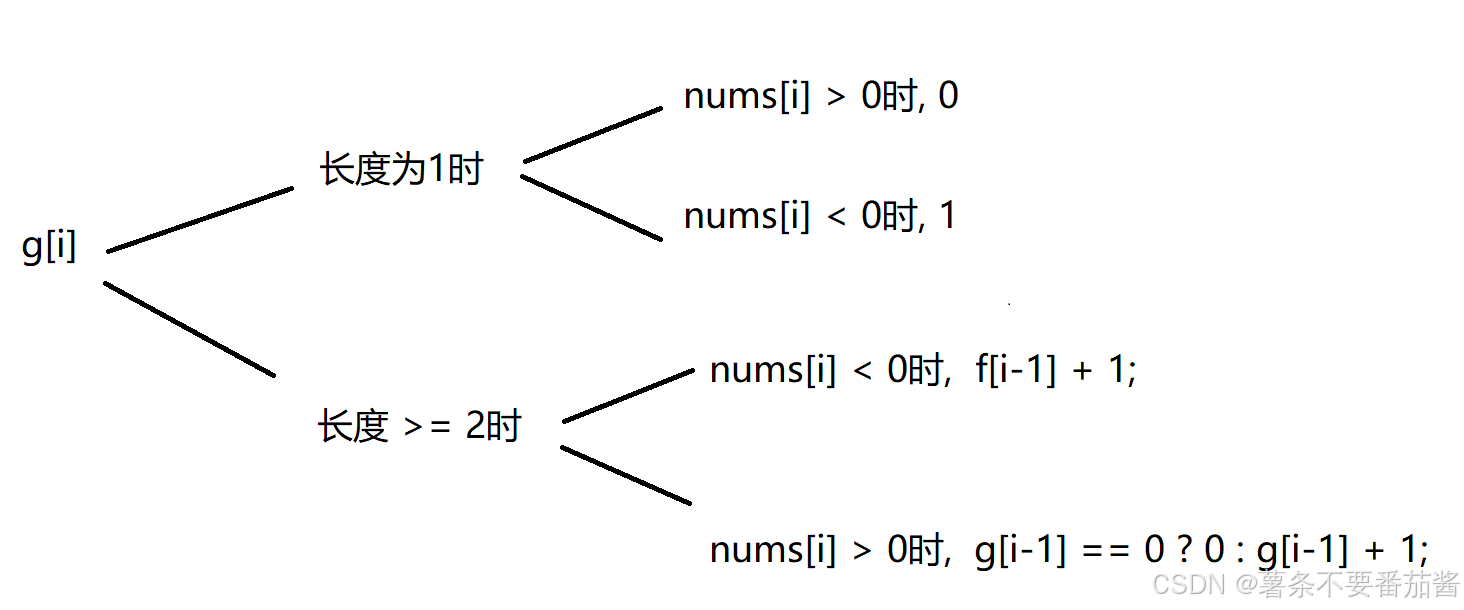本篇博客给大家带来的是子数组问题之动态规划解法技巧.
🐎文章专栏: 动态规划
🚀若有问题 评论区见
❤ 欢迎大家点赞 评论 收藏 分享
如果你不知道分享给谁,那就分享给薯条.
你们的支持是我不断创作的动力 .
要开心
要快乐
顺便进步
1. 最大子数组和
题目链接: 53. 最大子数组和
题目内容:
给你一个整数数组 nums ,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
子数组
是数组中的一个连续部分。
示例 1:
输入:nums = [-2,1,-3,4,-1,2,1,-5,4]
输出:6
解释:连续子数组 [4,-1,2,1] 的和最大,为 6 。
示例 2:
输入:nums = [1]
输出:1
示例 3:
输入:nums = [5,4,-1,7,8]
输出:23
提示:
1 <= nums.length <= 105
-104 <= nums[i] <= 104
第一 步骤分析
1. 状态表示
根据题目+做题经验分析得出
dp[i]表示以 i 位置为结尾, 所有子数组和中的最大和.
2. 状态转移方程
单个元素: dp[i] = nums[i];
两个元素以上: dp[i] = dp[i-1] + nums[i];
要求最大值,所以:
dp[i] = Math.max(nums[i],dp[i-1]+nums[i]);
3. 初始化
不多创建一个虚拟节点: 直接: dp[0] = nums[0];
创建虚拟节点: 处理两个细节
第一 初始化虚拟机点: dp[0] = 0, 这一步是为了保证填表的时候 dp[1] = nums[0];
第二 dp表与原数组之间的对应关系: dp[i] -> nums[i-1];
4. 填表顺序
从左往右
5. 返回值
整个dp表中的最大值.
第二 代码实现
class Solution {
public int maxSubArray(int[] nums) {
//不多创建一个虚拟节点
int n = nums.length;
int[] dp = new int[n];
if(n == 1) return nums[0];
dp[0] = nums[0];
int ret = -Integer.MAX_VALUE;
for(int i = 1;i < n;++i) {
dp[i] = Math.max(nums[i],dp[i-1]+nums[i]);
}
//只能填完表后重新遍历dp表比较得出最大值,因为在填表的循环中比较,dp[0]是不参与比较的.
for(int i = 0;i < n;++i) {
ret = Math.max(ret,dp[i]);
}
return ret;
//多创建一个虚拟节点
// int n = nums.length;
// int[] dp = new int[n+1];
// //初始化
// if(n == 1) return nums[0];
// dp[0] = 0;
// //填表
// int ret = -Integer.MAX_VALUE;
// for(int i = 1;i <= n;++i) {
// dp[i] = Math.max(nums[i-1],dp[i-1]+nums[i-1]);
// ret = Math.max(ret,dp[i]);
// }
// return ret;
}
}
2. 环形子数组的最大和
题目链接: 918. 环形子数组的最大和
题目内容:
给定一个长度为 n 的环形整数数组 nums ,返回 nums 的非空 子数组 的最大可能和 。
环形数组 意味着数组的末端将会与开头相连呈环状。形式上, nums[i] 的下一个元素是 nums[(i + 1) % n] , nums[i] 的前一个元素是 nums[(i - 1 + n) % n] 。
子数组 最多只能包含固定缓冲区 nums 中的每个元素一次。形式上,对于子数组 nums[i], nums[i + 1], …, nums[j] ,不存在 i <= k1, k2 <= j 其中 k1 % n == k2 % n 。
示例 1:
输入:nums = [1,-2,3,-2]
输出:3
解释:从子数组 [3] 得到最大和 3
示例 2:
输入:nums = [5,-3,5]
输出:10
解释:从子数组 [5,5] 得到最大和 5 + 5 = 10
示例 3:
输入:nums = [3,-2,2,-3]
输出:3
解释:从子数组 [3] 和 [3,-2,2] 都可以得到最大和 3
提示:
n == nums.length
1 <= n <= 3 * 104
-3 * 104 <= nums[i] <= 3 * 104
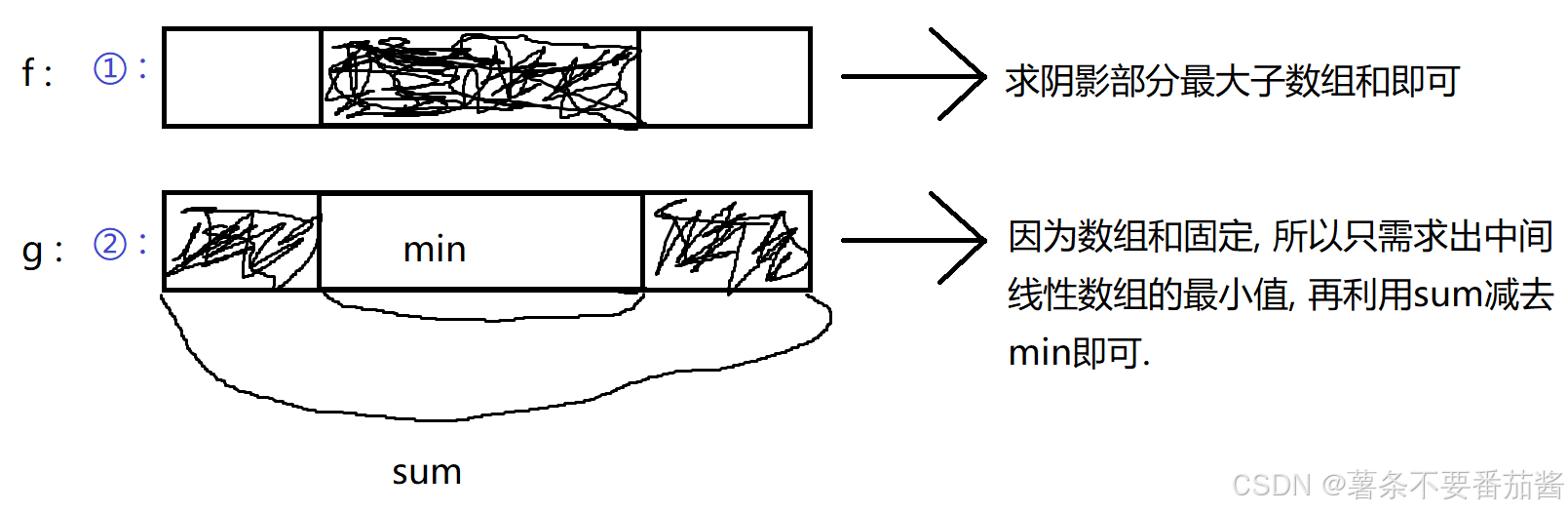
第一 预处理, 将环形数组问题转换成线性数组问题
子数组和最大值位置分布有两种可能,一是中间,二是两端,分这两种情况可以转换成求线性数组, 如下图:
第二 动态规划
1. 状态表示
f[i] 表示以 i 位置为结尾,所有子数组和中得最大值.
g[i] 表示以 i 位置为结尾, 所有子数组和中得最小值.
2. 状态转移方程
f[i] 与上道题一样有两种情况:
只有 i 一个元素 f[i] = nums[i];
有两个或以上元素 发f[i] = f[i-1] + nums[i];
f[i] = Math.max(nums[i],f[i-1]+nums[i]);
同理g[i] = Math.min(nums[i],g[i-1]+nums[i]);
3. 初始化
只讲多创建一个虚拟节点的初始化, 处理两个细节:
第一 dp表与原数组nums下标的对应关系: dp[i] -> nums[i-1]
第二 初始化虚拟节点: f[0] = 0; g[0] = 0x3f3f3f3f;(0x3f3f3f3f是最大值的一半, g[0]也可以初始化为最大值)
4. 填表顺序
从左到右
可分开填也可放在一个循环中填
5. 返回值
返回 [(f表最大值)与(sum-g表最小值)]中的最大值
第三 代码实现
class Solution {
public int maxSubarraySumCircular(int[] nums) {
//创建dp表
int n = nums.length;
int[] f = new int[n+1];
int[] g = new int[n+1];
//初始化
f[0] = 0;
g[0] = 0x3f3f3f3f;
//填表
int sum = 0;
for(int i = 0;i < n;++i) {
sum += nums[i];
}
int ret = -Integer.MAX_VALUE;
int tmp = -Integer.MAX_VALUE;
for(int i = 1;i <= n;++i) {
f[i] = Math.max(nums[i-1],f[i-1]+nums[i-1]);
g[i] = Math.min(nums[i-1],g[i-1]+nums[i-1]);
tmp = Math.max(tmp,f[i]);
ret = Math.max(ret,Math.max(f[i],sum-g[i]));
}
if(g[n] == sum) return tmp;
return ret;
}
}
3. 乘积最大子数组
题目链接: 152. 乘积最大子数组
题目内容:
给你一个整数数组 nums ,请你找出数组中乘积最大的非空连续
子数组
(该子数组中至少包含一个数字),并返回该子数组所对应的乘积。
测试用例的答案是一个 32-位 整数。
示例 1:
输入: nums = [2,3,-2,4]
输出: 6
解释: 子数组 [2,3] 有最大乘积 6。
示例 2:
输入: nums = [-2,0,-1]
输出: 0
解释: 结果不能为 2, 因为 [-2,-1] 不是子数组。
提示:
1 <= nums.length <= 2 * 104
-10 <= nums[i] <= 10
nums 的任何子数组的乘积都 保证 是一个 32-位 整数
第一 步骤分析
1. 状态表示
f[i] 表示 以 i 位置为结尾,所有子数组乘积中的最大值.
g[i] 表示以 i 位置为结尾,所有子数组乘积中的最小值.
本题第一次写状态表示是绝想不到要多定义一个g[i] 求最小值的, 得在写 f[i]的状态转移方程时才意识到 需要多求一个最小值g[i]. 此处我便直接给出, 可以自己先试试只定义f[i]去解.
2. 状态转移方程
先求f[i]:
若子数组长度为1, f[i] = nums[i];
若长度 >= 2 , f[i-1] × nums[i]; 但是nums[i] < 0的情况下, 最大值应该 = 最小值 × nums[i];
所以又细分为 nums[i] < 0, f[i] = g[i-1]×nums[i];
nums[i] > 0, f[i] = f[i-1]×nums[i];
三种情况取最大值
f[i] = Math.max(nums[i] , Math.max(g[i-1]×nums[i],f[i-1]×nums[i]) );
同理g[i] = Math.max(nums[i] , Math.max(g[i-1]×nums[i],f[i-1]×nums[i]) );
3. 初始化
多创建一个虚拟节点,处理两个细节:
第一 dp表与nums数组下标的对应关系:
dp[i] -> nums[i-1];
第二 初始化虚拟节点:
f[0] = 1; g[0] = 1;
4. 填表顺序
从左往右同时填
5. 返回值
返回 f 表中的最大值.
第二 代码实现
class Solution {
public int maxProduct(int[] nums) {
int n = nums.length;
int[] f = new int[n+1];
int[] g = new int[n+1];
//初始化
f[0] = g[0] = 1;
//填表
int ret = -Integer.MAX_VALUE;
for(int i = 1;i <= n;++i) {
f[i] = Math.max(nums[i-1],Math.max(f[i-1]*nums[i-1],g[i-1]*nums[i-1]));
g[i] = Math.min(nums[i-1],Math.min(g[i-1]*nums[i-1],f[i-1]*nums[i-1]));
ret = Math.max(ret,f[i]);
}
return ret;
}
}
4. 乘积为正数的最长子数组长度
题目链接: 1567. 乘积为正数的最长子数组长度
题目内容:
给你一个整数数组 nums ,请你求出乘积为正数的最长子数组的长度。
一个数组的子数组是由原数组中零个或者更多个连续数字组成的数组。
请你返回乘积为正数的最长子数组长度。
示例 1:
输入:nums = [1,-2,-3,4]
输出:4
解释:数组本身乘积就是正数,值为 24 。
示例 2:
输入:nums = [0,1,-2,-3,-4]
输出:3
解释:最长乘积为正数的子数组为 [1,-2,-3] ,乘积为 6 。
注意,我们不能把 0 也包括到子数组中,因为这样乘积为 0 ,不是正数。
示例 3:
输入:nums = [-1,-2,-3,0,1]
输出:2
解释:乘积为正数的最长子数组是 [-1,-2] 或者 [-2,-3] 。
第一 步骤分析
1. 状态表示
f[i] 表示 以 i 位置为结尾 所有子数组乘积为正数的最长长度.
g[i] 表示 以 i 位置为结尾 所有子数组乘积为负数的最长长度.(刚开始同样不知道还要g[i], 在第二步写f[i] 的状态转移方程的时候才意识到的)
2. 状态转移方程
先求f[i], f[i]表示的是子数组乘积正数的最长长度, 与nums[i] 的正负有关:
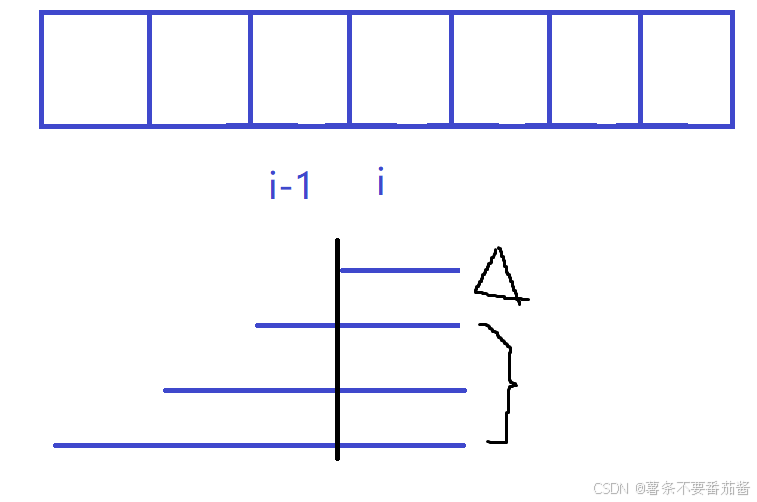
当子数组长度为 1 时, 若nums[i] > 0时, f[i] = 1; 若nums[i] < 0时, f[i] = 0;
当子数组长度为 2 时, 若nums[i] > 0时, f[i] = f[i-1] + 1; 若nums[i] < 0时, f[i] = g[i-1] == 0 ? 0 : g[i-1] + 1;
f[i] 表示的是最大值, 所以:
当nums[i] > 0时, 只考虑 f[i] = f[i-1] + 1; 因为f[i-1] + 1 >= 1的.
当nums[i] < 0时, 只考虑 f[i] = g[i-1] == 0 ? 0 : g[i-1] + 1;
再求g[i]:
g[i] 是最大值:
当nums[i] > 0时, g[i] = g[i-1] == 0 ? 0 : g[i-1] + 1;
当nums[i] < 0时, g[i] = f[i-1] + 1;
3. 初始化
多创建一个虚拟节点, 处理两个细节:
第一 dp表与原数组nums下标之间的对应关系: dp[i] -> nums[i-1]
第二 初始化虚拟节点: f[0] = 0 保证填表时,若nums[i-1] > 0; f[1] =1;
g[0] = 0 保证填表时, 若nums[i-1] < 0; g[1] = 1;
4. 填表顺序
从左到右,两个表同时填.
5. 返回值
返回 f 表中的最大值.
第二 代码实现
class Solution {
public int getMaxLen(int[] nums) {
int n = nums.length;
//建表
int[] f = new int[n+1];
int[] g = new int[n+1];
//初始化虚拟节点
//默认为0即可
//填表
int ret = -Integer.MAX_VALUE;
for(int i = 1;i <= n;++i) {
if(nums[i-1] > 0) {
f[i] = f[i-1] + 1;
g[i] = g[i-1] == 0 ? 0 : g[i-1]+1;
}else if(nums[i-1] < 0) {
f[i] = g[i-1] == 0 ? 0 : g[i-1]+1;
g[i] = f[i-1] + 1;
}
ret = Math.max(ret,f[i]);
}
return ret;
}
}
本篇博客到这里就结束啦, 感谢观看 ❤❤❤
🐎期待与你的下一次相遇😊😊😊