本篇博客给大家带来的是01背包问题之动态规划解法技巧.
🐎文章专栏: 动态规划
🚀若有问题 评论区见
❤ 欢迎大家点赞 评论 收藏 分享
如果你不知道分享给谁,那就分享给薯条.
你们的支持是我不断创作的动力 .
要开心
要快乐
顺便进步
1. 01背包
题目链接: DP41 【模板】01背包
题目内容:
描述
示例1
输入:
3 5
2 10
4 5
1 4
输出:
14
9
说明:
装第一个和第三个物品时总价值最大,但是装第二个和第三个物品可以使得背包恰好装满且总价值最大。
示例2
输入:
3 8
12 6
11 8
6 8
输出:
8
0
说明:
装第三个物品时总价值最大但是不满,装满背包无解。
备注:
要求O(nV)的时间复杂度,O(V)空间复杂度
第一Ⅰ问的动态规划
1. 状态表示
01背包问题本质上还是 线性dp问题,按线性dp来定义状态即可.
第Ⅰ问: 尝试一维定义
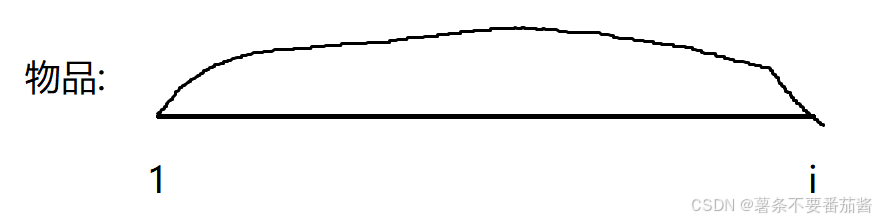
dp[i] 表示在前 i 个位置中选择物品, 在所有的选法中, 物品总体积不超过背包容量V 时的最大价值.
上述一维定义在写状态转移方程时不能保证所选物品体积不会超过背包的容量,并且选完之后背包剩余容量也时未知的.一维定义解决不了问题,
用二维定义dp[i][j] 表示在前 i 个位置中选择物品, 物品总体积不超过 V的所有选法中能选出来的最大价值.
2. 状态转移方程
根据最后一个位置是否选择, 来划分问题:
① i 物品不选, dp[i] = dp[i-1][j]
② i 物品要选, 需要保证剩余容量大于等于0, j-v[i]>= 0, w[i] + dp[i-1][j-v[i]];
3. 初始化
选择物品是从下标1 开始的, 到n结束, 那么dp表就需要多创建一行一列,处理两个细节问题:
①下标之间的对应关系: i -> i j -> j
②初始化虚拟节点:
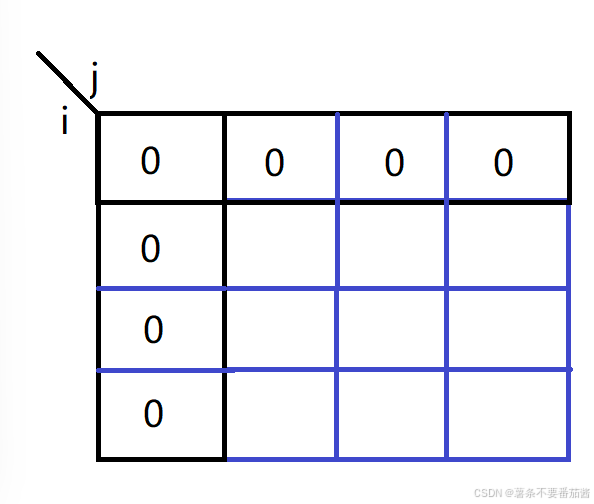
第一行表示的是 物品可选,总体积不超过 j 的最大价值. 既然没有物品,那就不选,全都为0.
第一列表示的是 所选物品总体积不超过0的最大价值. 此时最大价值就是0,不选即可,全都为0.
4. 填表顺序
根据状态转移方程可知,要想得到dp[i][j] 就得先知道dp[i-1][j]或者dp[i-1][j-v[i]],
所以应该从上往下填写每一行
从左往右填写每一列.
5. 返回值
打印 dp[n][V]即可.
第二 Ⅱ问的动态规划
1. 状态表示
与第Ⅰ问同样的分析方法:
二维定义dp[i][j] 表示在前 i 个位置中选择物品, 物品总体积刚好为 V的所有选法中能选出来的最大价值.
可能存在所有选法都不能恰好装满背包,我们规定此时dp[i][j] = -1;
2. 状态转移方程
根据最后一个位置是否选择, 来划分问题:
① i 物品不选, dp[i] = dp[i-1][j]
② i 物品要选, 需要保证剩余容量大于等于0, j-v[i]>= 0, w[i] + dp[i-1][j-v[i]];
3. 初始化
选择物品是从下标1 开始的, 到n结束, 那么dp表就需要多创建一行一列,处理两个细节问题:
①下标之间的对应关系: i -> i j -> j
②初始化虚拟节点:
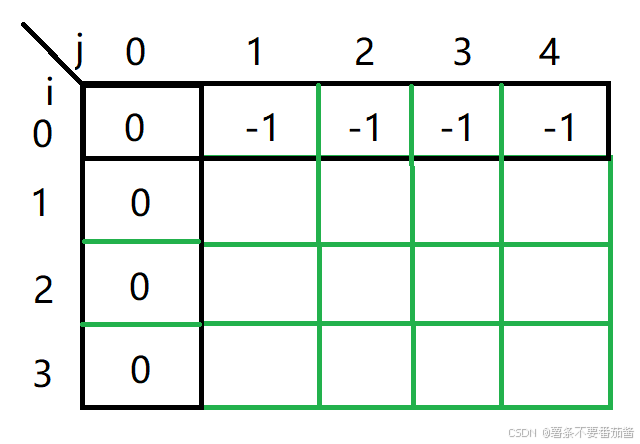
第一行表示的是 没有物品可选,总体积等于 j 的最大价值.dp[0][0] = 0, 后面 无论选不选,总价值都达不到 j ,于是全都初始化为-1.
第一列表示的是 所选物品总体积等于0的最大价值. 此时最大价值就是0,不选即可,全都为0.
4. 填表顺序
根据状态转移方程可知,要想得到dp[i][j] 就得先知道dp[i-1][j]或者dp[i-1][j-v[i]],
所以应该从上往下填写每一行
从左往右填写每一列.
5. 返回值
打印 dp[n][V]即可.
第三 优化
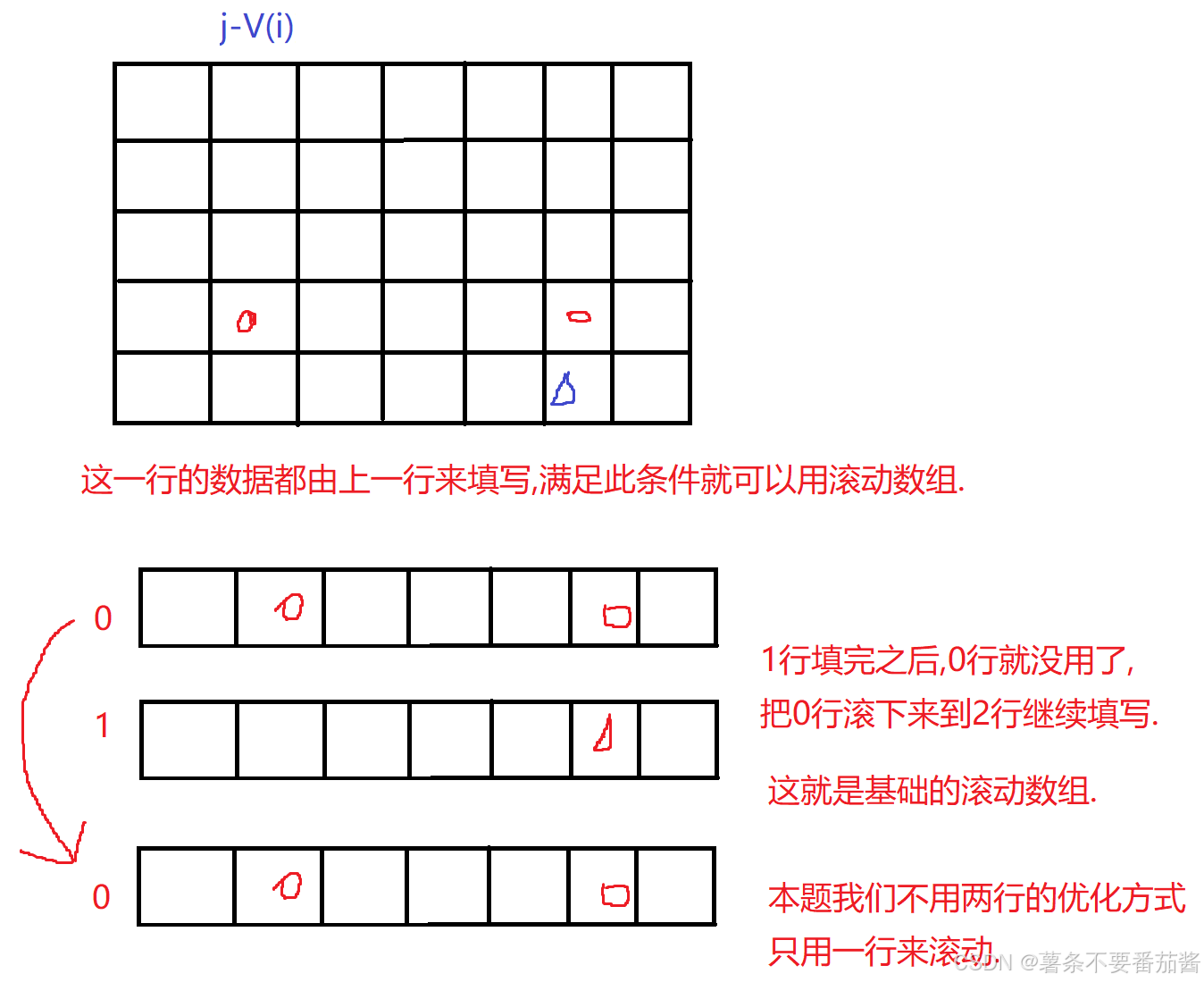
①利用滚动数组做空间上的优化
②直接在原始代码上修改
Ⅰ删除所有的 i 维
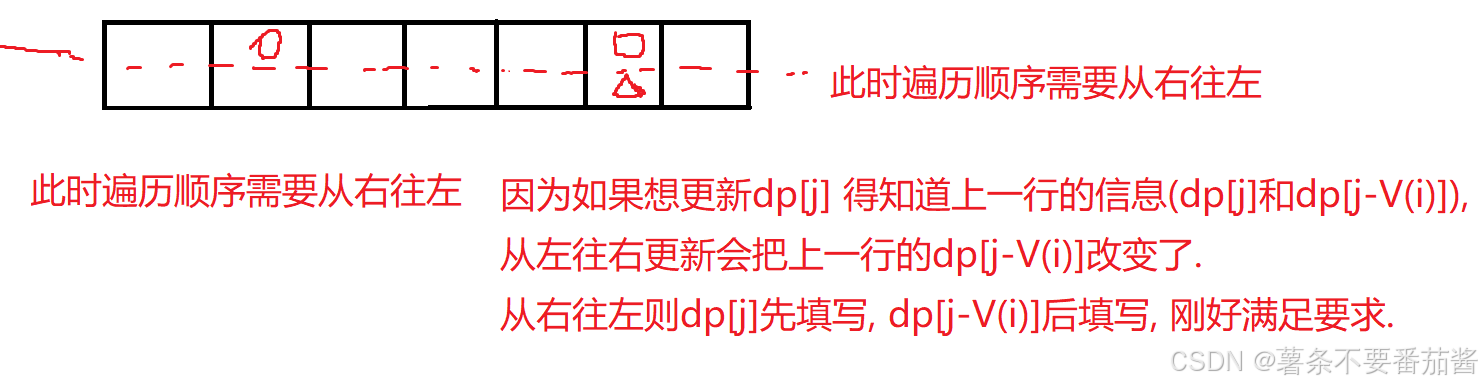
(★)Ⅱ 填表时从右往左遍历 j .
第四 代码实现
// //优化前:
// Scanner in = new Scanner(System.in);
// int N = 1010;
// // 注意 hasNext 和 hasNextLine 的区别
// int n = in.nextInt();
// int V = in.nextInt();
// int[][] dp1 = new int[N][N];
// int[][] dp2 = new int[N][N];
// int[] v = new int[N];
// int[] w = new int[N];
// for (int i = 1; i <= n; ++i) {
// v[i] = in.nextInt();
// w[i] = in.nextInt();
// }
// //1.解决第一个问题(1)求这个背包至多能装多大价值的物品?
// //填表
// for (int i = 1; i <= n; ++i) {
// for (int j = 0; j <= V; ++j) { //修改遍历顺序
// dp1[i][j] = dp1[i-1][j];
// if(j >= v[i]) {
// dp1[i][j] = Math.max(dp1[i][j], w[i] + dp1[i-1][j - v[i]]);
// }
// }
// }
// System.out.println(dp1[n][V]);
// //2. 解决第二个问题 (2)若背包恰好装满,求至多能装多大价值的物品?
// for (int i = 1; i <= V; ++i) {
// dp2[0][i] = -1;
// }
// for (int i = 1; i <= n; ++i) {
// for (int j = 0; j <= V; ++j) {
// dp2[i][j] = dp2[i-1][j];
// if (j-v[i] >= 0 && dp2[i-1][j - v[i]] != -1) {
// dp2[i][j] = Math.max(dp2[i][j], w[i] + dp2[i-1][j - v[i]]);
// }
// }
// }
// //若是-1则输出0, 若不是则正常输出.
// System.out.println((dp2[n][V] == -1 ? 0 : dp2[n][V]));
//优化后:
Scanner in = new Scanner(System.in);
int N = 1010;
// 注意 hasNext 和 hasNextLine 的区别
int n = in.nextInt();
int V = in.nextInt();
int[] dp1 = new int[N];
int[] dp2 = new int[N];
int[] v = new int[N];
int[] w = new int[N];
for (int i = 1; i <= n; ++i) {
v[i] = in.nextInt();
w[i] = in.nextInt();
}
//1.解决第一个问题(1)求这个背包至多能装多大价值的物品?
//填表
for (int i = 1; i <= n; ++i) {
for (int j = V; j >= v[i]; --j) { //修改遍历顺序
dp1[j] = Math.max(dp1[j], w[i] + dp1[j - v[i]]);
}
}
System.out.println(dp1[V]);
//2. 解决第二个问题 (2)若背包恰好装满,求至多能装多大价值的物品?
for (int i = 1; i <= V; ++i) {
dp2[i] = -1;
}
for (int i = 1; i <= n; ++i) {
for (int j = V; j >= v[i]; --j) {
if (dp2[j - v[i]] != -1) {
dp2[j] = Math.max(dp2[j], w[i] + dp2[j - v[i]]);
}
}
}
//若是-1则输出0, 若不是则正常输出.
System.out.println((dp2[V] == -1 ? 0 : dp2[V]));
2. 分割等和子集
题目链接: 416. 分割等和子集
题目内容:
给你一个 只包含正整数 的 非空 数组 nums 。请你判断是否可以将这个数组分割成两个子集,使得两个子集的元素和相等。
示例 1:
输入:nums = [1,5,11,5]
输出:true
解释:数组可以分割成 [1, 5, 5] 和 [11] 。
示例 2:
输入:nums = [1,2,3,5]
输出:false
解释:数组不能分割成两个元素和相等的子集。
提示:
1 <= nums.length <= 200
1 <= nums[i] <= 100
第一 预处理
直接去判断两个子集的元素和是否相等会有点复杂, 可以转化为只研究一个子集等于原数组元素和的一半, 即在数组中选择一些数, 这些数的和是否等于原数组元素和的一半.
第二 动态规划
1. 状态表示
根据第一题模板题可知定义状态的方式:
dp[i][j]表示在nums的前 i 个位置中选择一些数,所有选法中,是否存在一些数,使得这些数之和为 j.
2. 状态转移方程
根据最后一个位置nums[i]是否选择来划分情况:
①nums[i]不选: dp[i][j] = dp[i-1][j];
②nums[i]要选: 需要保证所选数之和不超过 j . j - nums[i] >= 0, dp[i][j-nums[i]];
3. 初始化
dp表多创建一行一列,需要处理两个问题:
①dp表与nums表元素之间的对应关系:
i -> i-1; j -> j-1
②初始化虚拟节点(就是多创建的一行一列),保证填表的正确性:
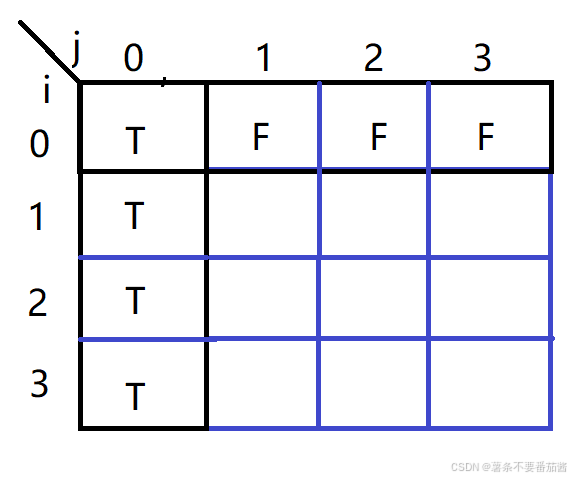
第一行 i=0意味着没有元素可选,怎么选最大值都只能是0,所以dp[0][0] = true,其余全部初始化为false.
第一列 j=0意味着需要凑成和为0, 直接不选即可. 故从i=1开始全部初始化为true.
4. 填表顺序
根据状态转移方程可知,要想求得dp[i][j]就得先知道dp[i-1][j]和dp[i-1][j-nums[i]],所以可知填表顺序为:
从上往下填写每一行
每一行从左往右填写
5. 返回值
返回dp[nums.length][原数组元素和的一半]
第三 优化
①利用滚动数组做空间上的优化
②直接在原始代码上修改
Ⅰ删除所有的 i 维
(★)Ⅱ 填表时从右往左遍历 j .
第四 代码实现
class Solution {
public boolean canPartition(int[] nums) {
// int n = nums.length;
// int sum = 0;
// for(int x : nums) sum += x;
// if(sum%2 == 1) return false;
// int aim = sum/2;
// boolean[][] dp = new boolean[n+1][aim+1];
// for(int i = 0;i <= n;++i) {
// dp[i][0] = true;
// }
// for(int i = 1;i <= n;++i) {
// if(i < n) {
// sum += nums[i];
// }
// for(int j = 1;j <= aim;++j) {
// dp[i][j] = dp[i-1][j];
// if(j >= nums[i-1] && dp[i][j] == false) {
// dp[i][j] = dp[i-1][j-nums[i-1]];
// }
// }
// }
// return dp[n][aim];
// }
//优化: 删除第一维, 从右往左遍历第二维
int n = nums.length;
int sum = 0;
for(int x : nums) sum += x;
if(sum%2 == 1) return false;
int aim = sum/2;
boolean[] dp = new boolean[aim+1];
dp[0] = true;
for(int i = 1;i <= n;++i) {
if(i < n) {
sum += nums[i];
}
for(int j = aim;j >= nums[i-1];--j) { //修改遍历顺序,本质上是滚动数组的优化.
if(dp[j] == false) {
dp[j] = dp[j-nums[i-1]];
}
}
}
return dp[aim];
}
}
本篇博客到这里就结束啦, 感谢观看 ❤❤❤
🐎期待与你的下一次相遇😊😊😊