不久前我写了一篇AES加密算法,但它属于高级加密标准。今天我们来聊一聊数据加密算法,即DES。
引言
首先我们先了解一下DES的发展历史,数据加密标准是美国IBM公司的研究人员Horst Feistel和Walter Tuchman于20世纪70年代中期提出的一个密码算法(LUCIFER算法(金星算法))的基础上发展而来的,并于1977年1月15日由美国国家标准局(NBS)正式公布实施,是第一个公开的商用密码算法标准,并得到了IOS的认可。在过去的40多年里,DES被广泛的应用于美国联邦和各种商业信息的安全保密工作中,经受了各种密码分析和攻击,体现出来令人满意的安全性。但随着密码分析技术和计算机计算能力的提高,DES算法不再安全。1994年,美国决定于1998年12月之后不再使用DES算法,在2000年,DES算法已经被更为安全的AES算法,即高级加密标准所取代。虽然这样,目前还无法将DES算法完全、彻底地破解,而且DES算法的加解密过程非常快,仍是当前使用最为常见的分组密码算法。
算法流程
1.初始置换(IP)
操作流程:
①输入64bit的明文块
②按照初始置换表进行置换
| 58 | 50 | 42 | 34 | 26 | 18 | 10 | 2 |
| 60 | 52 | 44 | 36 | 28 | 20 | 12 | 4 |
| 62 | 54 | 46 | 38 | 30 | 22 | 14 | 6 |
| 64 | 56 | 48 | 40 | 32 | 24 | 16 | 8 |
| 57 | 49 | 41 | 33 | 25 | 17 | 9 | 1 |
| 59 | 51 | 43 | 35 | 27 | 19 | 11 | 3 |
| 61 | 53 | 45 | 37 | 29 | 21 | 13 | 5 |
| 63 | 55 | 47 | 39 | 31 | 23 | 15 | 7 |
例:
输入的64 bits的明文块为01100011 01101111 01101101 0111000 0111010 01110100 01100101 01110010按照初始置换(IP)表进行置换。置换过程是输入的64bit明文块根据 置换表中的下表位置进行置换。
输入明文块的第1个bit为0,在置换表中找到1的位置为第5行第8列,将该bit填充至该位置
输入明文块的第40个bit为0,在置换表中找到40的位置为第4行第4列,将该bit填充至该位置
那么输出为多少呢?
输出该置换表的内容的步骤为:从第一行开始输出,一行输出完成后再输出下一行
故输出为:11111111 10111000 01110110 01010111 00000000 11111111 00000110 10000011
读者可以自行计算一下,是否理解了该过程。
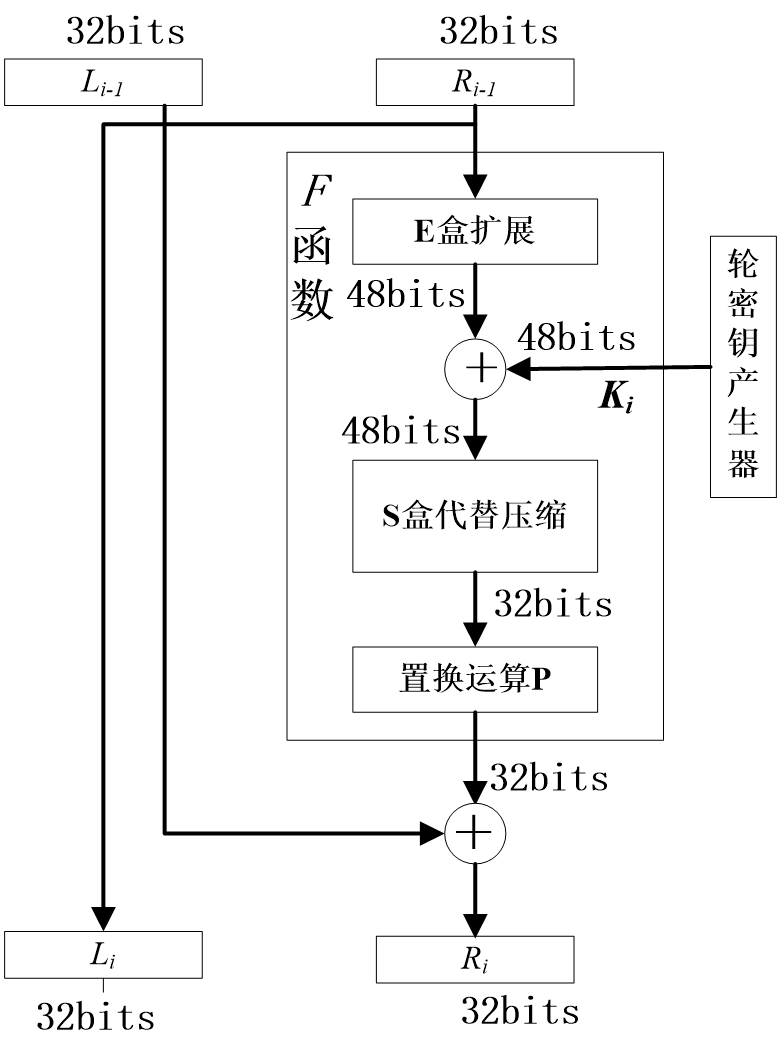
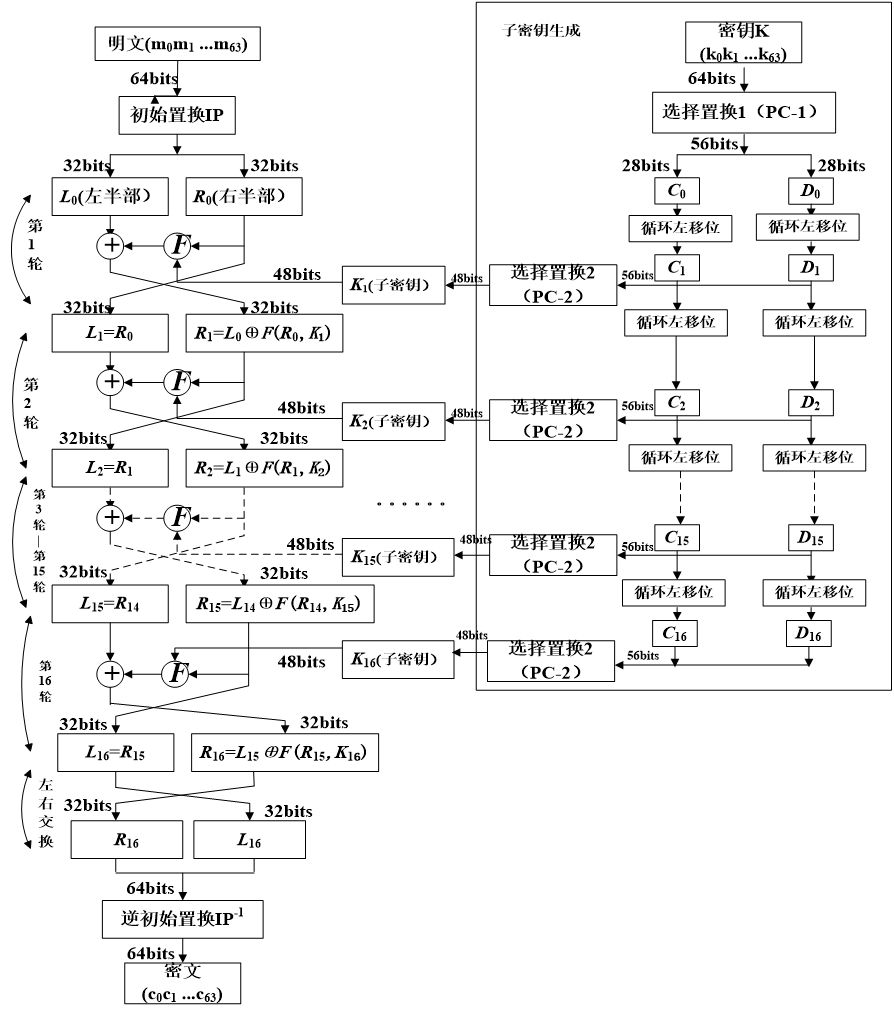
2.轮结构
操作流程:
①将IP置换后的64bit分为两部分,前32bit为左部分,记作L0,后32bit为右部分,记作R0
②下一轮的左部分是上一轮的右部分,下一轮的右部分为上一轮右部分与轮密钥Ki进行一次F函数变换,变换的结果再与上一轮左部分进行异或运算得到
③重复①②,总共进行16轮轮变换
以下是一轮变换示意图:
接下来我们对F函数进行详细的解析:
如示意图所示,F函数的第一个变换为E盒扩展
(1)E盒扩展
E盒扩展就是对输入的某些位进行扩展和置换,将32bit扩展为48bit,E盒扩展方式与初始置换类似
| 32 | 1 | 2 | 3 | 4 | 5 |
| 4 | 5 | 6 | 7 | 8 | 9 |
| 8 | 9 | 10 | 11 | 12 | 13 |
| 12 | 13 | 14 | 15 | 16 | 17 |
| 16 | 17 | 18 | 19 | 20 | 21 |
| 20 | 21 | 22 | 23 | 24 | 25 |
| 24 | 25 | 26 | 27 | 28 | 29 |
| 28 | 29 | 30 | 31 | 32 | 1 |
都是将对应位置的bit在E盒扩展表中找到对应位置填入,此处我不再对此进行赘述,填入方法参考初始置换(IP)
那么输出呢?
输出方式也于初始置换(IP)类似,此处不再赘述
例:
E盒输入的32 bits为R0=0000 0000 1111 1111 0000 0110 1000 0011,经过E盒扩展之后,得到的48 bits输出:100000 000001 011111 111110 100000 001101 010000 000110。
读者可以自行计算一下,是否理解该过程。
经过E盒扩展后得到48bit,我们要采取什么措施将其压缩至32bit方便下一轮右部分的产生呢?
(2)子密钥异或运算
我们将经过E盒扩展后的48bit输出与对应的48bit子密钥进行异或运算
例:
假设48 bits子密钥K1=01010000001011001010110001010100 0010001101000111,则异或操作如下:
输入: 100000 000001 011111 111110 100000 001101 010000 000110
子密钥: 010100 000010 110010 101100 010101 000010 001101 000111
输出: 110100 000011 101101 010010 110101 001111 011101 000001
读者可以自行计算一下,是否理解该过程。
(3)S盒替代
将异或运算后的48bit分为6组,每组8bit分别进入S盒进行代替压缩,最终实现将E盒扩展的48bit转换成32bit。S盒代替是DES算法的唯一一个非线性变换,是保证DES算法安全性的源泉。DES算法总共有8个固定的S盒,一个S盒 有16列和4行,每个元素4bit,通常用10进制表示。
每个S盒的使用方法为:S盒接受6bit后,6bit中的第1个bit和最后1个bit构成两位二进制数为该S盒的行号,6bit中间的4个bit二进制为该S盒的列号,然后根据行号和列号在对应的S盒中查找对应的值(一般为10进制数),该值就是S盒变换的输出,并转化为2进制数。
例:
若S盒输入的48 bits为110100 000011 101101 010010 110101 001111 011101 000001,则分成8组,每组6 bits,则对应的各S盒的行和列号如下:
| S盒 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 输入 | 110100 | 000011 | 101101 | 010010 | 110101 | 001111 | 011101 | 000001 |
| 行 | 2 | 1 | 3 | 0 | 3 | 1 | 1 | 1 |
| 列 | 10 | 1 | 6 | 9 | 10 | 7 | 14 | 0 |
| 查表值 | 9 | 13 | 8 | 2 | 0 | 5 | 8 | 1 |
| 输出 | 1001 | 1101 | 1000 | 0010 | 0000 | 0101 | 1000 | 0001 |
因此经过S盒作用,输出32 bits为:10011101100000100000010110000001。
读者可以自行计算一下,是否理解该过程。
(4)P盒置换
S盒压缩代替之后,输出的32bit作为F函数的最后变换P盒置换输入,P盒置换操作与初始置换(IP)类似,此处不再赘述。
| 16 | 7 | 20 | 21 |
| 29 | 12 | 28 | 17 |
| 1 | 15 | 23 | 26 |
| 5 | 18 | 31 | 10 |
| 2 | 8 | 24 | 14 |
| 32 | 27 | 3 | 9 |
| 19 | 13 | 30 | 6 |
| 22 | 11 | 4 | 25 |
例:
P盒置换输入:1001 1101 1000 0010 0000 0101 1000 0001 P盒置换输出:0000 0000 1100 1000 0110 1001 0001 1011
读者可以自行计算一下,是否理解该过程。
3.逆初始置换(IP-1)
DES在完成16轮变换后,得到的64bit数据作为IP-1逆初始置换的输入,经过IP-1逆初始置换表将64bit输入数据位置进行重现编排,得到输出64bit数据,为最终密文。
逆初始置换与初始置换类似,此处不再赘述
| 40 | 8 | 48 | 16 | 56 | 24 | 64 | 32 |
| 39 | 7 | 47 | 15 | 55 | 23 | 63 | 31 |
| 38 | 6 | 46 | 14 | 54 | 22 | 62 | 30 |
| 37 | 5 | 45 | 13 | 53 | 21 | 61 | 29 |
| 36 | 4 | 44 | 12 | 52 | 20 | 60 | 28 |
| 35 | 3 | 43 | 11 | 51 | 19 | 59 | 27 |
| 34 | 2 | 42 | 10 | 50 | 18 | 58 | 26 |
| 33 | 1 | 41 | 9 | 49 | 17 | 57 | 25 |
例:
输入逆初始置换的64bit为:11111111 10111000 01110110 01010111 00000000 11111111 00000110 10000011,按照逆初始置换表操作后,输出为:01100011 01101111 01101101 01110000 01110101 01110100 01100101 01110010
读者可以自行计算一下,是否理解该过程。
4.DES算法子密钥生成过程
DES算法规定密钥长度为64bit,其中有效密钥长度为56bit,在DES子密钥生成算法中直接使用,另外8bit在算法中不直接使用,可作为校验位。
操作流程:
①置换选择PC-1
通过置换选择PC-1,将初始密钥的8bit奇偶校验位去掉,并重新编排,留下真正的56bit有效位。置换选择PC-1与初始置换类似,此处不再赘述。
| 57 | 49 | 41 | 33 | 25 | 17 | 9 |
| 1 | 58 | 50 | 42 | 34 | 26 | 18 |
| 10 | 2 | 59 | 51 | 43 | 35 | 27 |
| 19 | 11 | 3 | 60 | 52 | 44 | 36 |
| 63 | 55 | 47 | 39 | 31 | 33 | 15 |
| 7 | 62 | 54 | 46 | 38 | 30 | 22 |
| 14 | 6 | 61 | 53 | 45 | 37 | 29 |
| 21 | 13 | 5 | 28 | 20 | 12 | 4 |
例:
输入: 00110000 00110001 00110010 00110011 00110100 00110101 00110110 00110111
输出: 00000000 00000000 11111111 11111100 11001111 00000000 00001111
读者可以自行计算一下,是否理解该过程。
②循环左移
将PC-1置换输出的56bit数据分位两组,每组28bit,分别记作C0与D0,再分别经过一个循环左移函数,每部分循环左移1或2位(每轮次移位位数不同),记作C1与D1
例:
前28 bits为C0=0000 0000 0000 0000 1111 1111 1111
后28 bits为D0=1100 1100 1111 0000 0000 0000 1111
然后根据左循环移位函数进行左循环移位1或2位,各轮循环左移位位数如表所示。
根据表所示,C0及D0分别左循环1位得到
C1=000 0000 0000 0000 1111 1111 1111 0,
D1=100 1100 1111 0000 0000 0000 1111 1。
读者可以自行计算一下,是否理解该过程。
③置换选择PC-2
将C1 与D1连接成56bit数据作为置换选择PC-2的输入,根据置换选择PC-2表重新进行编排和压缩,得到48bit的子密钥k1,而C1与D1作为下一轮子密钥的输入。
| 14 | 17 | 11 | 24 | 1 | 5 |
| 3 | 28 | 15 | 6 | 21 | 10 |
| 23 | 19 | 12 | 4 | 26 | 8 |
| 16 | 7 | 27 | 20 | 13 | 2 |
| 41 | 52 | 31 | 37 | 47 | 55 |
| 30 | 40 | 51 | 45 | 33 | 48 |
| 44 | 49 | 39 | 56 | 34 | 53 |
| 46 | 42 | 50 | 36 | 29 | 32 |
例:
将C1和D1连接,56 bits为000 0000 0000 0000 1111 1111 1111 0 100 1100 1111 0000 0000 0000 1111 1作为置换选择PC-2的输入。
输出:01010000 00101100 10101100 01010100 00100011 01000111
读者可以自行计算一下,是否理解该过程。