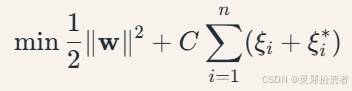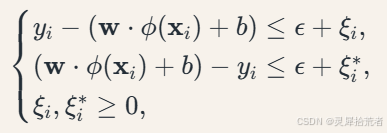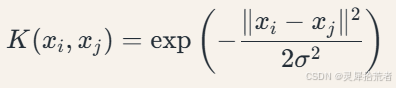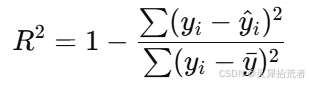一、前言

        随着人工智能技术的不断发展，机器学习已成为各类复杂问题建模与预测的重要工具。本文以支持向量机（Support Vector Machine, SVM）为核心，针对回归任务展开分析，涵盖数据预处理、模型训练、预测与评估全流程。通过MATLAB代码实例，详细展示了如何利用SVM解决回归问题，适用于房价预测、销量预测等实际场景。文中将深入解析SVM的数学原理、代码实现细节及模型评估方法，为读者提供完整的机器学习建模参考。

二、技术与原理简介

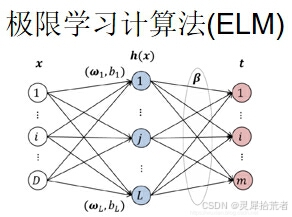
        极限学习机（ELM, Extreme Learning Machine）是一种高效的前馈神经网络训练算法，特别适用于回归和分类问题。ELM具有以下特点：

        1. 随机性：ELM网络中的隐藏层参数是随机生成的，且不需要迭代优化。

        2. 速度：由于隐藏层权重是随机的，因此训练速度极快。

        3. 理论保证：在一定的条件下，ELM能够近似任意的连续函数。

        其核心公式如下：

        目标函数：

        约束条件：

其中，𝑤 为权重向量；𝐶 为正则化参数；𝜉𝑖 ​为松弛变量；𝜖 为容忍偏差；𝜙(⋅) 为核函数映射。

        高斯核函数（RBF）：

         代码中采用高斯核（RBF核）处理非线性关系：

        高斯核通过带宽参数𝜎 控制样本间相似性的衰减速度。

三、代码详解

        本文的 MATLAB 代码主要分为以下几个部分：

        1. 数据加载与预处理

clear,clc;close all;tic
load data1 data1
rng(43,'twister')
N=length(data1);  
temp=randperm(N);
ttt=2;ppp=950;f_=ttt;
P_train = data1(temp(1: ppp), 1: ttt)';
T_train = data1(temp(1: ppp), ttt+1)';
M = size(P_train, 2);

P_test = data1(temp(ppp+1: end), 1: ttt)';
T_test = data1(temp(ppp+1: end), ttt+1)';
N = size(P_test, 2);

说明：

• 通过 load 加载数据，并利用 randperm 随机打乱顺序，确保样本的随机性。
• 按照预设的样本数（前 950 个为训练集，其余为测试集）划分数据。
• 数据转置后以列向量形式存储，便于后续矩阵计算。

        2. 数据归一化及转置

%%  数据归一化
[p_train, ps_input] = mapminmax(P_train, 0, 1);
p_test = mapminmax('apply', P_test, ps_input);

[t_train, ps_output] = mapminmax(T_train, 0, 1);
t_test = mapminmax('apply', T_test, ps_output); 

%%  转置以适应模型
p_train = p_train'; p_test = p_test';
t_train = t_train'; t_test = t_test';

说明：

• 使用 mapminmax 函数将数据缩放到 [0,1] 区间，这有助于提高网络训练的稳定性和收敛速度。
• 分别对输入数据和目标数据进行归一化处理，后续在仿真测试时再将结果反归一化还原。

        3. 模型创建、训练

%% 模型训练
Mdl = fitrsvm(p_train,t_train,'KernelFunction','gaussian');  

说明：

• 功能：训练SVM回归模型，使用高斯核（RBF）处理非线性关系。
• 参数说明：KernelFunction指定核函数类型，'gaussian'对应RBF核。

        4. 仿真测试与数据反归一化

%%  模型预测
t_sim1=predict(Mdl,p_train);  %训练集预测结果	
t_sim2=predict(Mdl,p_test);  %测试集预测结果			

%%  数据反归一化
T_sim1 = mapminmax('reverse', t_sim1, ps_output);
T_sim2 = mapminmax('reverse', t_sim2, ps_output);
T_sim1=T_sim1';T_sim2=T_sim2';

说明：

• 使用 sim 函数分别对训练集和测试集进行预测，获取模型输出。
• 通过 mapminmax('reverse', ...) 将归一化后的预测结果反归一化，恢复到原始数据尺度，便于与真实值比较。

        5. 性能评价指标计算

%% 计算评价指标
error1 = sqrt(sum((T_sim1 - T_train).^2) ./ M);  % 训练集 RMSE
error2 = sqrt(sum((T_test - T_sim2).^2) ./ N);     % 测试集 RMSE

R1 = 1 - norm(T_train - T_sim1)^2 / norm(T_train - mean(T_train))^2; % 训练集 R²
R2 = 1 - norm(T_test - T_sim2)^2 / norm(T_test - mean(T_test))^2;      % 测试集 R²

mse1 = sum((T_sim1 - T_train).^2) ./ M;  % 训练集 MSE
mse2 = sum((T_sim2 - T_test).^2) ./ N;     % 测试集 MSE

SE1 = std(T_sim1 - T_train);
RPD1 = std(T_train) / SE1;               % 训练集剩余预测残差

SE = std(T_sim2 - T_test);
RPD2 = std(T_test) / SE;                 % 测试集 RPD

MAE1 = mean(abs(T_train - T_sim1));       % 训练集 MAE
MAE2 = mean(abs(T_test - T_sim2));        % 测试集 MAE

MAPE1 = mean(abs((T_train - T_sim1) ./ T_train)); % 训练集 MAPE
MAPE2 = mean(abs((T_test - T_sim2) ./ T_test));    % 测试集 MAPE

MBE1 = sum(T_sim1 - T_train) ./ M;        % 训练集 MBE
MBE2 = sum(T_sim2 - T_test) ./ N;         % 测试集 MBE

说明：

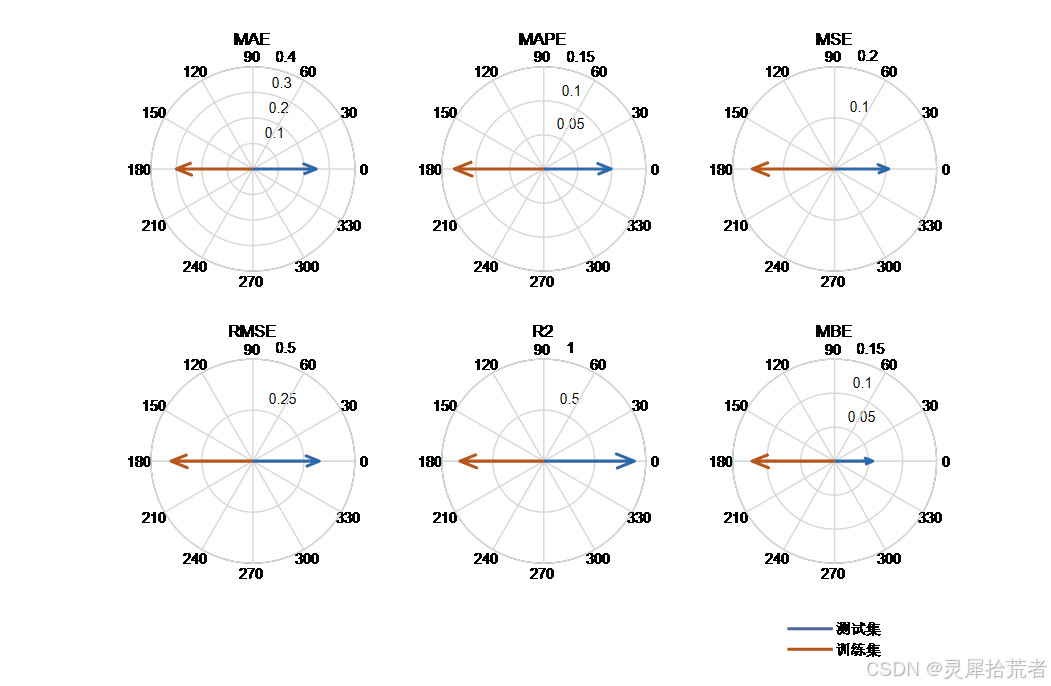
• 利用多种指标（RMSE、𝑅2 、MSE、RPD、MAE、MAPE、MBE）对模型在训练集和测试集上的表现进行定量评估。
• 决定系数 𝑅2 的计算公式为：

其中 𝑦𝑖 为实际值，𝑦^𝑖 为预测值，𝑦ˉ 为实际值的均值。

        6. 完整代码

clear,clc;close all;tic
load data1 data1
rng(43,'twister')
N=length(data1);  
temp=randperm(N);
ttt=2;ppp=950;f_=ttt;
P_train = data1(temp(1: ppp), 1: ttt)';
T_train = data1(temp(1: ppp), ttt+1)';
M = size(P_train, 2);

P_test = data1(temp(ppp+1: end), 1: ttt)';
T_test = data1(temp(ppp+1: end), ttt+1)';
N = size(P_test, 2);

%%  数据归一化
[p_train, ps_input] = mapminmax(P_train, 0, 1);
p_test = mapminmax('apply', P_test, ps_input);

[t_train, ps_output] = mapminmax(T_train, 0, 1);
t_test = mapminmax('apply', T_test, ps_output); 

%%  转置以适应模型
p_train = p_train'; p_test = p_test';
t_train = t_train'; t_test = t_test';

%% 模型训练
Mdl = fitrsvm(p_train,t_train,'KernelFunction','gaussian');     		

%%  模型预测
t_sim1=predict(Mdl,p_train);  %训练集预测结果	
t_sim2=predict(Mdl,p_test);  %测试集预测结果			

%%  数据反归一化
T_sim1 = mapminmax('reverse', t_sim1, ps_output);
T_sim2 = mapminmax('reverse', t_sim2, ps_output);
T_sim1=T_sim1';T_sim2=T_sim2';

%%  均方根误差 RMSE
error1 = sqrt(sum((T_sim1 - T_train).^2)./M);
error2 = sqrt(sum((T_test - T_sim2).^2)./N);
%% 决定系数
R1 = 1 - norm(T_train - T_sim1)^2 / norm(T_train - mean(T_train))^2;
R2 = 1 - norm(T_test -  T_sim2)^2 / norm(T_test -  mean(T_test ))^2;
%% 均方误差 MSE
mse1 = sum((T_sim1 - T_train).^2)./M;
mse2 = sum((T_sim2 - T_test).^2)./N;
%% RPD 剩余预测残差
SE1=std(T_sim1-T_train);
RPD1=std(T_train)/SE1;
SE=std(T_sim2-T_test);
RPD2=std(T_test)/SE;
%% 平均绝对误差MAE
MAE1 = mean(abs(T_train - T_sim1));
MAE2 = mean(abs(T_test - T_sim2));
%% 平均绝对百分比误差MAPE
MAPE1 = mean(abs((T_train - T_sim1)./T_train));
MAPE2 = mean(abs((T_test - T_sim2)./T_test));
%% 平均偏差误差MBE
MBE1 = sum(T_sim1 - T_train) ./ M ;
MBE2 = sum(T_sim2 - T_test ) ./ N ;

四、总结与思考

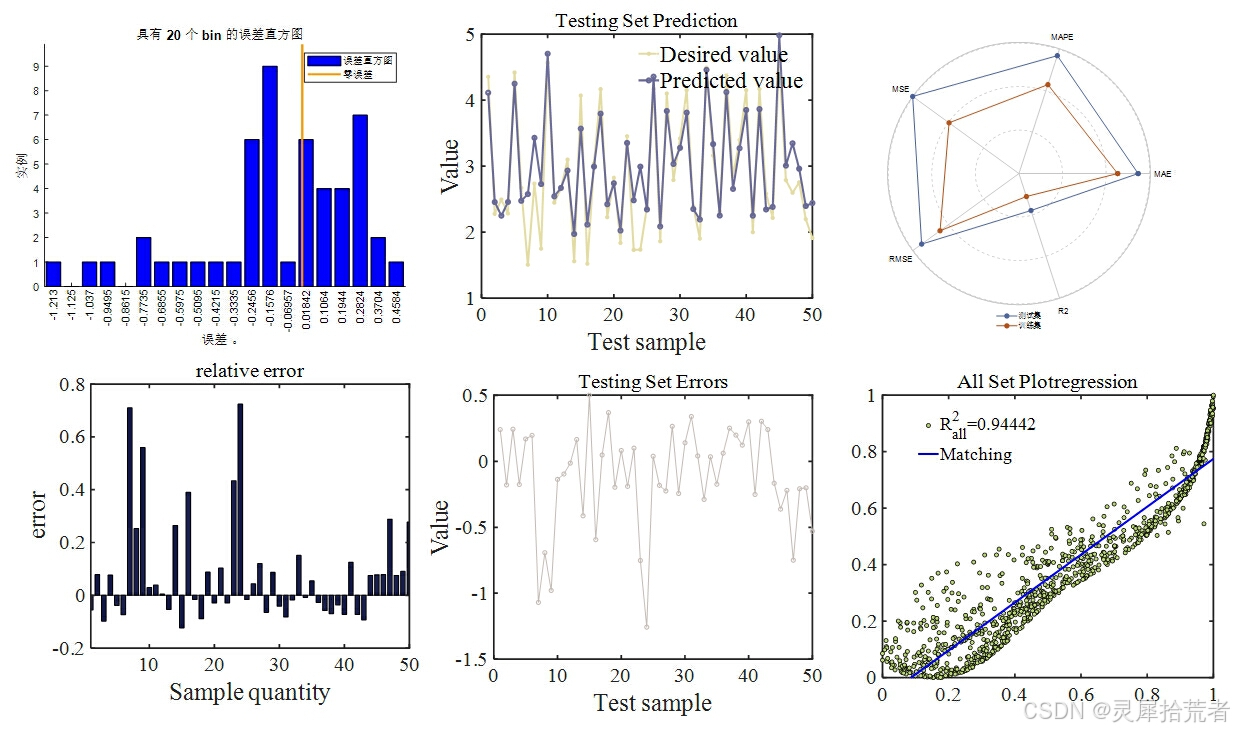
        本文通过详细的代码实现和分段讲解，展示了基于 MATLAB 平台的 SVM 极限学习机在数据拟合问题中的应用。实验结果表明，通过交叉验证确定最佳隐含层节点数，所构建的 SVM 极限学习机在训练集与测试集上均获得了较低的误差和较高的决定系数，表明其具备优秀的拟合能力和泛化性能。
        从实际应用角度看，该方法为非线性数据建模提供了一种有效的解决方案，但仍需注意数据预处理、参数选择等环节对模型性能的影响。未来研究可进一步探讨网络结构改进、参数优化以及多模型集成等方向，以实现更高的预测精度和稳定性。

【作者声明】

        本文内容基于作者对 MATLAB SVM 极限学习机实现过程的实验与总结，所有数据和代码均为原创。文章中的观点仅代表个人见解，供读者参考交流。若有任何问题或建议，欢迎在评论区留言讨论，共同促进技术进步。

【关注我们】

        如果您对神经网络、群智能算法及人工智能技术感兴趣，请关注我们的公众号，获取更多前沿技术文章、实战案例及技术分享！欢迎点赞、收藏并转发，与更多朋友一起探讨与交流！点赞+收藏+关注，后台留言可获免费资源及相关数据集。