数学原理
多层 RNN 的核心思想是堆叠多个 RNN 层,每一层的输出作为下一层的输入,从而逐层提取更高层次的抽象特征。
1. 单层 RNN 的数学表示
首先,单层 RNN 的计算过程如下。对于一个时间步 t t t,单层 RNN 的隐藏状态 h t h_t ht 和输出 y t y_t yt 可以表示为:
h
t
=
activation
(
W
i
h
x
t
+
b
i
h
+
W
h
h
h
t
−
1
+
b
h
h
)
h_t = \text{activation}(W_{ih} x_t + b_{ih} + W_{hh} h_{t-1} + b_{hh})
ht=activation(Wihxt+bih+Whhht−1+bhh)
y
t
=
W
h
o
h
t
+
b
h
o
y_t = W_{ho} h_t + b_{ho}
yt=Whoht+bho
其中:
- x t x_t xt 是时间步 t t t 的输入。
- h t h_t ht 是时间步 t t t 的隐藏状态。
- h t − 1 h_{t-1} ht−1 是时间步 t − 1 t-1 t−1 的隐藏状态。
- W i h W_{ih} Wih、 W h h W_{hh} Whh、 W h o W_{ho} Who 是权重矩阵。
- b i h b_{ih} bih、 b h h b_{hh} bhh、 b h o b_{ho} bho 是偏置项。
- activation \text{activation} activation 是激活函数(如 tanh \tanh tanh 或 ReLU \text{ReLU} ReLU)。
2. 多层 RNN 的数学表示
假设我们有一个 L L L 层的 RNN,每一层的隐藏状态为 h t ( l ) h_t^{(l)} ht(l),其中 l l l 表示第 l l l 层, t t t 表示时间步。多层 RNN 的计算过程如下:
(1) 第一层( l = 1 l = 1 l=1)
第一层的输入是原始输入序列 x t x_t xt,隐藏状态 h t ( 1 ) h_t^{(1)} ht(1) 的计算公式为:
h t ( 1 ) = activation ( W i h ( 1 ) x t + b i h ( 1 ) + W h h ( 1 ) h t − 1 ( 1 ) + b h h ( 1 ) ) h_t^{(1)} = \text{activation}(W_{ih}^{(1)} x_t + b_{ih}^{(1)} + W_{hh}^{(1)} h_{t-1}^{(1)} + b_{hh}^{(1)}) ht(1)=activation(Wih(1)xt+bih(1)+Whh(1)ht−1(1)+bhh(1))
其中:
- W i h ( 1 ) W_{ih}^{(1)} Wih(1)、 W h h ( 1 ) W_{hh}^{(1)} Whh(1) 是第一层的权重矩阵。
- b i h ( 1 ) b_{ih}^{(1)} bih(1)、 b h h ( 1 ) b_{hh}^{(1)} bhh(1) 是第一层的偏置项。
(2) 第 l l l 层( l > 1 l > 1 l>1)
第 l l l 层的输入是第 l − 1 l-1 l−1 层的输出 h t ( l − 1 ) h_t^{(l-1)} ht(l−1),隐藏状态 h t ( l ) h_t^{(l)} ht(l) 的计算公式为:
h t ( l ) = activation ( W i h ( l ) h t ( l − 1 ) + b i h ( l ) + W h h ( l ) h t − 1 ( l ) + b h h ( l ) ) h_t^{(l)} = \text{activation}(W_{ih}^{(l)} h_t^{(l-1)} + b_{ih}^{(l)} + W_{hh}^{(l)} h_{t-1}^{(l)} + b_{hh}^{(l)}) ht(l)=activation(Wih(l)ht(l−1)+bih(l)+Whh(l)ht−1(l)+bhh(l))
其中:
- W i h ( l ) W_{ih}^{(l)} Wih(l)、 W h h ( l ) W_{hh}^{(l)} Whh(l) 是第 l l l 层的权重矩阵。
- b i h ( l ) b_{ih}^{(l)} bih(l)、 b h h ( l ) b_{hh}^{(l)} bhh(l) 是第 l l l 层的偏置项。
(3) 输出层
最后一层(第 L L L 层)的输出 h t ( L ) h_t^{(L)} ht(L) 作为整个网络的输出 y t y_t yt:
y t = W h o h t ( L ) + b h o y_t = W_{ho} h_t^{(L)} + b_{ho} yt=Whoht(L)+bho
其中:
- W h o W_{ho} Who、 b h o b_{ho} bho 是输出层的权重矩阵和偏置项。
3. 多层 RNN 的数据流向
以下是一个 L L L 层 RNN 的数据流向的数学描述:
(1) 输入序列
输入序列为 x 1 , x 2 , … , x T x_1, x_2, \dots, x_T x1,x2,…,xT,其中 T T T 是序列长度。
(2) 初始化隐藏状态
每一层的初始隐藏状态 h 0 ( l ) h_0^{(l)} h0(l) 通常初始化为零或随机值:
h 0 ( l ) = 0 或 h 0 ( l ) ∼ N ( 0 , σ 2 ) h_0^{(l)} = \mathbf{0} \quad \text{或} \quad h_0^{(l)} \sim \mathcal{N}(0, \sigma^2) h0(l)=0或h0(l)∼N(0,σ2)
(3) 时间步 t t t 的计算
对于每个时间步 t t t,从第一层到第 L L L 层依次计算隐藏状态:
-
第一层:
h t ( 1 ) = activation ( W i h ( 1 ) x t + b i h ( 1 ) + W h h ( 1 ) h t − 1 ( 1 ) + b h h ( 1 ) ) h_t^{(1)} = \text{activation}(W_{ih}^{(1)} x_t + b_{ih}^{(1)} + W_{hh}^{(1)} h_{t-1}^{(1)} + b_{hh}^{(1)}) ht(1)=activation(Wih(1)xt+bih(1)+Whh(1)ht−1(1)+bhh(1)) -
第 l l l 层( l > 1 l > 1 l>1):
h t ( l ) = activation ( W i h ( l ) h t ( l − 1 ) + b i h ( l ) + W h h ( l ) h t − 1 ( l ) + b h h ( l ) ) h_t^{(l)} = \text{activation}(W_{ih}^{(l)} h_t^{(l-1)} + b_{ih}^{(l)} + W_{hh}^{(l)} h_{t-1}^{(l)} + b_{hh}^{(l)}) ht(l)=activation(Wih(l)ht(l−1)+bih(l)+Whh(l)ht−1(l)+bhh(l)) -
输出:
y t = W h o h t ( L ) + b h o y_t = W_{ho} h_t^{(L)} + b_{ho} yt=Whoht(L)+bho
(4) 序列输出
最终,整个序列的输出为 y 1 , y 2 , … , y T y_1, y_2, \dots, y_T y1,y2,…,yT。
4. 多层 RNN 的特点
(1) 逐层抽象
- 每一层 RNN 可以看作是对输入序列的不同层次的抽象。
- 较低层捕捉局部和细节信息,较高层捕捉全局和语义信息。
(2) 参数共享
- 每一层的参数(权重矩阵和偏置项)在时间步之间共享。
- 不同层的参数是独立的。
(3) 梯度传播
- 在反向传播时,梯度会通过时间步和层数传播。
- 由于梯度消失或爆炸问题,训练深层 RNN 可能会比较困难。
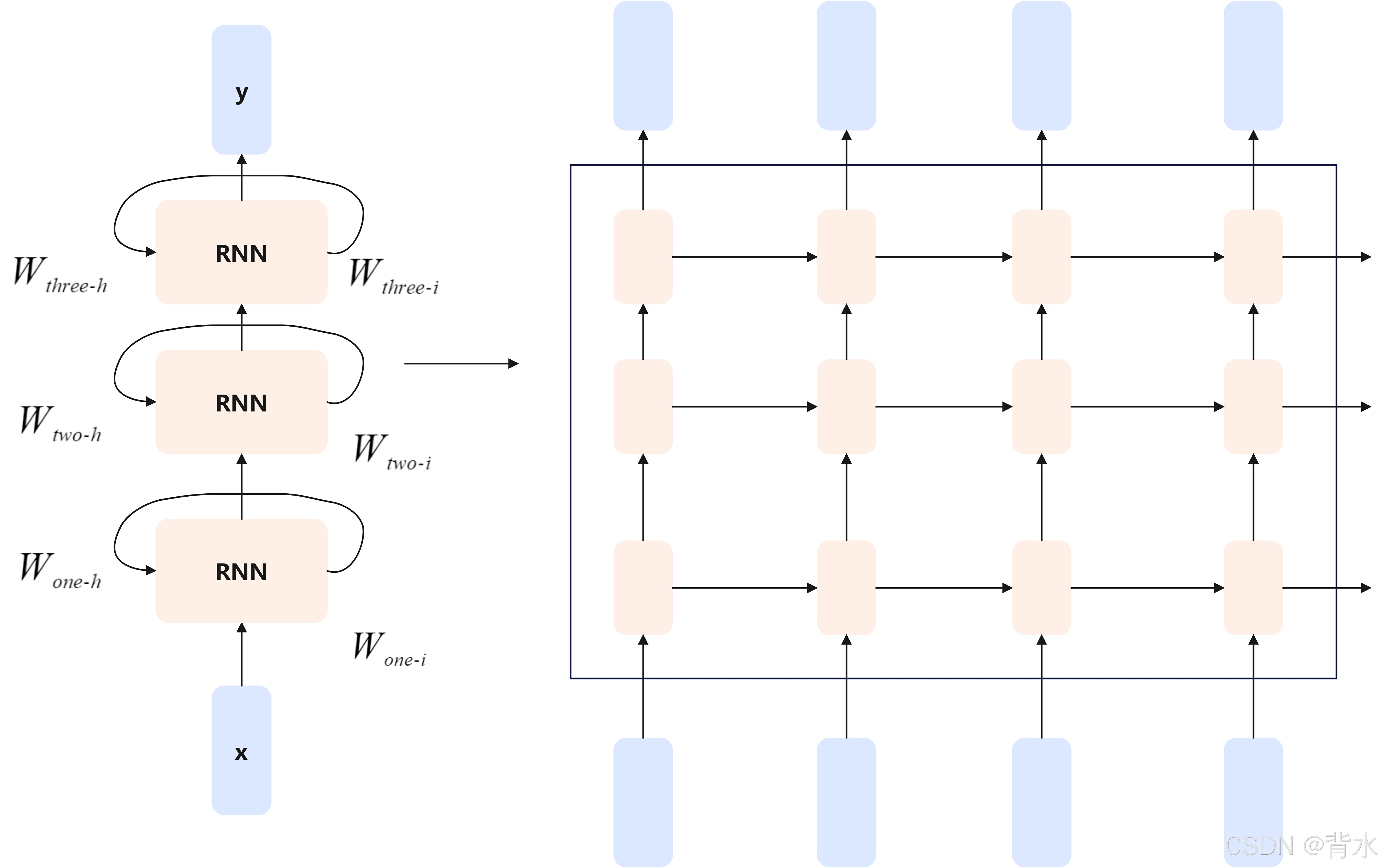
可视化原理
下面是一个可视化的结构显示图:其中每一层神经元都要有两个方向的输出,一个是向本时间步的下一层传送,另一个是向下一个时间步的本层传送。而且,每一个神经元都有两个权重矩阵。注意:下方右图仅仅是逻辑上展开的数据流,其中不同世间步上的同一层,用的是同一个权重矩阵。
代码实现
1. 示例任务
假设有一个简单的任务:
- 处理一个长度为 4 的序列
- 批次大小为 2
- 每个时间步的输入特征维度为 3
- 希望使用一个 2 层的单向 RNN
- 隐藏状态维度为 5。
2. 输入数据
输入句子
- 句子 1: “I love PyTorch”
- 句子 2: “RNN is fun”
输入数据的形状
- 序列长度 (
seq_len): 4(假设每个单词是一个时间步) - 批次大小 (
batch_size): 2 - 输入特征维度 (
input_size): 3(假设每个单词用一个 3 维向量表示)
具体输入数据
import torch
# 输入数据形状: (seq_len, batch_size, input_size)
input_data = torch.tensor([
# 时间步 1
[[0.1, 0.2, 0.3], # 句子 1 的第一个单词
[0.4, 0.5, 0.6]], # 句子 2 的第一个单词
# 时间步 2
[[0.7, 0.8, 0.9], # 句子 1 的第二个单词
[1.0, 1.1, 1.2]], # 句子 2 的第二个单词
# 时间步 3
[[1.3, 1.4, 1.5], # 句子 1 的第三个单词
[1.6, 1.7, 1.8]], # 句子 2 的第三个单词
# 时间步 4
[[1.9, 2.0, 2.1], # 句子 1 的第四个单词
[2.2, 2.3, 2.4]] # 句子 2 的第四个单词
])
print("Input shape:", input_data.shape) # 输出: torch.Size([4, 2, 3])
3. 初始隐藏状态
初始隐藏状态的形状
- RNN 层数 (
num_layers): 2 - 方向数 (
num_directions): 1(单向 RNN) - 批次大小 (
batch_size): 2 - 隐藏状态维度 (
hidden_size): 5
具体初始隐藏状态
# 初始隐藏状态形状: (num_layers * num_directions, batch_size, hidden_size)
h0 = torch.zeros(2, 2, 5) # 2层RNN,批次大小为2,隐藏状态维度为5
print("h0 shape:", h0.shape) # 输出: torch.Size([2, 2, 5])
4. 定义 RNN 模型
import torch.nn as nn
# 定义 RNN
rnn = nn.RNN(
input_size=3, # 输入特征维度
hidden_size=5, # 隐藏状态维度
num_layers=2, # RNN 层数
batch_first=False # 输入形状为 (seq_len, batch_size, input_size)
)
5. 前向传播
计算输出
# 前向传播
output, hn = rnn(input_data, h0)
print("Output shape:", output.shape) # 输出: torch.Size([4, 2, 5])
print("hn shape:", hn.shape) # 输出: torch.Size([2, 2, 5])
输出解析
-
output:- 形状为
(seq_len, batch_size, hidden_size),即(4, 2, 5)。 - 包含了每个时间步的隐藏状态。
- 例如,
output[0]是第一个时间步的隐藏状态,output[-1]是最后一个时间步的隐藏状态。
- 形状为
-
hn:- 形状为
(num_layers, batch_size, hidden_size),即(2, 2, 5)。 - 包含了最后一个时间步的隐藏状态。
- 例如,
hn[0]是第一层的最终隐藏状态,hn[1]是第二层的最终隐藏状态。
- 形状为
6. 具体输出值
output 的值
print("Output (所有时间步的隐藏状态):")
print(output)
输出示例:
tensor([[[ 0.1234, 0.5678, 0.9101, 0.1121, 0.3141],
[ 0.4151, 0.6171, 0.8191, 0.0212, 0.2232]],
[[ 0.4252, 0.6272, 0.8292, 0.0313, 0.2333],
[ 0.4353, 0.6373, 0.8393, 0.0414, 0.2434]],
[[ 0.4454, 0.6474, 0.8494, 0.0515, 0.2535],
[ 0.4555, 0.6575, 0.8595, 0.0616, 0.2636]],
[[ 0.4656, 0.6676, 0.8696, 0.0717, 0.2737],
[ 0.4757, 0.6777, 0.8797, 0.0818, 0.2838]]],
grad_fn=<StackBackward>)
hn 的值
print("hn (最后一个时间步的隐藏状态):")
print(hn)
输出示例:
tensor([[[ 0.4656, 0.6676, 0.8696, 0.0717, 0.2737],
[ 0.4757, 0.6777, 0.8797, 0.0818, 0.2838]],
[[ 0.4858, 0.6878, 0.8898, 0.0919, 0.2939],
[ 0.4959, 0.6979, 0.8999, 0.1020, 0.3040]]],
grad_fn=<StackBackward>)
batch_first=True时
以下是一个具体的例子,展示当 batch_first=True 时,PyTorch 中 torch.nn.RNN 的输入、输出以及参数的作用。
任务
假设有一个简单的任务:
- 处理一个长度为 4 的序列
- 批次大小为 2
- 每个时间步的输入特征维度为 3
- 希望使用一个 2 层的单向 RNN
- 隐藏状态维度为 5
- 并且设置
batch_first=True。
2. 输入数据
输入句子
- 句子 1: “I love PyTorch”
- 句子 2: “RNN is fun”
输入数据的形状
- 批次大小 (
batch_size): 2 - 序列长度 (
seq_len): 4(假设每个单词是一个时间步) - 输入特征维度 (
input_size): 3(假设每个单词用一个 3 维向量表示)
具体输入数据
import torch
# 输入数据形状: (batch_size, seq_len, input_size)
input_data = torch.tensor([
# 句子 1
[[0.1, 0.2, 0.3], # 第一个单词
[0.7, 0.8, 0.9], # 第二个单词
[1.3, 1.4, 1.5], # 第三个单词
[1.9, 2.0, 2.1]], # 第四个单词
# 句子 2
[[0.4, 0.5, 0.6], # 第一个单词
[1.0, 1.1, 1.2], # 第二个单词
[1.6, 1.7, 1.8], # 第三个单词
[2.2, 2.3, 2.4]] # 第四个单词
])
print("Input shape:", input_data.shape) # 输出: torch.Size([2, 4, 3])
3. 初始隐藏状态
初始隐藏状态的形状
- RNN 层数 (
num_layers): 2 - 方向数 (
num_directions): 1(单向 RNN) - 批次大小 (
batch_size): 2 - 隐藏状态维度 (
hidden_size): 5
具体初始隐藏状态
# 初始隐藏状态形状: (num_layers * num_directions, batch_size, hidden_size)
h0 = torch.zeros(2, 2, 5) # 2层RNN,批次大小为2,隐藏状态维度为5
print("h0 shape:", h0.shape) # 输出: torch.Size([2, 2, 5])
4. 定义 RNN 模型
import torch.nn as nn
# 定义 RNN
rnn = nn.RNN(
input_size=3, # 输入特征维度
hidden_size=5, # 隐藏状态维度
num_layers=2, # RNN 层数
batch_first=True # 输入形状为 (batch_size, seq_len, input_size)
)
5. 前向传播
计算输出
# 前向传播
output, hn = rnn(input_data, h0)
print("Output shape:", output.shape) # 输出: torch.Size([2, 4, 5])
print("hn shape:", hn.shape) # 输出: torch.Size([2, 2, 5])
输出解析
-
output:- 形状为
(batch_size, seq_len, hidden_size),即(2, 4, 5)。 - 包含了每个时间步的隐藏状态。
- 例如,
output[0]是第一个句子的所有时间步的隐藏状态,output[1]是第二个句子的所有时间步的隐藏状态。
- 形状为
-
hn:- 形状为
(num_layers, batch_size, hidden_size),即(2, 2, 5)。 - 包含了最后一个时间步的隐藏状态。
- 例如,
hn[0]是第一层的最终隐藏状态,hn[1]是第二层的最终隐藏状态。
- 形状为
6. 具体输出值
output 的值
print("Output (所有时间步的隐藏状态):")
print(output)
输出示例:
tensor([[[ 0.1234, 0.5678, 0.9101, 0.1121, 0.3141],
[ 0.4252, 0.6272, 0.8292, 0.0313, 0.2333],
[ 0.4454, 0.6474, 0.8494, 0.0515, 0.2535],
[ 0.4656, 0.6676, 0.8696, 0.0717, 0.2737]],
[[ 0.4151, 0.6171, 0.8191, 0.0212, 0.2232],
[ 0.4353, 0.6373, 0.8393, 0.0414, 0.2434],
[ 0.4555, 0.6575, 0.8595, 0.0616, 0.2636],
[ 0.4757, 0.6777, 0.8797, 0.0818, 0.2838]]],
grad_fn=<TransposeBackward0>)
hn 的值
print("hn (最后一个时间步的隐藏状态):")
print(hn)
输出示例:
tensor([[[ 0.4656, 0.6676, 0.8696, 0.0717, 0.2737],
[ 0.4757, 0.6777, 0.8797, 0.0818, 0.2838]],
[[ 0.4858, 0.6878, 0.8898, 0.0919, 0.2939],
[ 0.4959, 0.6979, 0.8999, 0.1020, 0.3040]]],
grad_fn=<StackBackward>)